
二次函数是确定的,但它的定义域区间是随参数t而变化的,我们称这种情况是“定函数在动区间上的最值”。
例5. 如果函数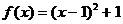 定义在区间
定义在区间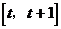 上,求
上,求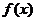 的最小值。
的最小值。
解:函数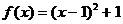 ,其对称轴方程为
,其对称轴方程为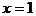 ,顶点坐标为(1,1),图象开口向上。
,顶点坐标为(1,1),图象开口向上。
如图6所示,若顶点横坐标在区间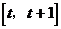 左侧时,有
左侧时,有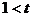 。当
。当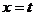 时,函数取得最小值
时,函数取得最小值
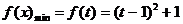 。
。
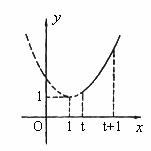
图6
如图7所示,若顶点横坐标在区间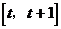 上时,有
上时,有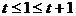 ,即
,即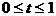 。当
。当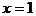 时,函数取得最小值
时,函数取得最小值
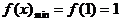 。
。
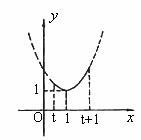
图7
如图8所示,若顶点横坐标在区间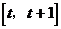 右侧时,有
右侧时,有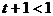 ,即
,即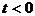 。当
。当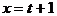 时,函数取得最小值
时,函数取得最小值
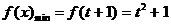
综上讨论,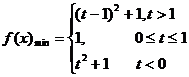
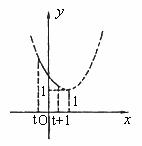
图8
例6. 设函数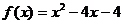 的定义域为
的定义域为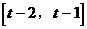 ,对任意
,对任意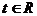 ,求函数
,求函数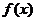 的最小值
的最小值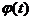 的解析式。
的解析式。
解:将二次函数配方得:
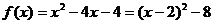
其对称轴方程为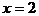 ,顶点坐标为
,顶点坐标为 ,图象开口向上
,图象开口向上
若顶点横坐标在区间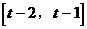 左侧,则
左侧,则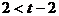 ,即
,即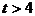 。当
。当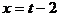 时,函数取得最小值
时,函数取得最小值
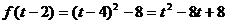
若顶点横坐标在区间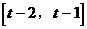 上,则
上,则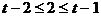 ,即
,即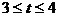 。当
。当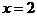 时,函数取得最小值
时,函数取得最小值
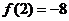
若顶点横坐标在区间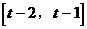 右侧,则
右侧,则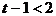 ,即
,即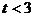 。当
。当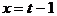 时,函数取得最小值
时,函数取得最小值
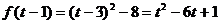
综上讨论,得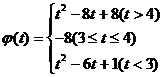
二次函数随着参数a的变化而变化,即其图象是运动的,但定义域区间是固定的,我们称这种情况是“动二次函数在定区间上的最值”。
例3. 已知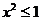 ,且
,且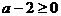 ,求函数
,求函数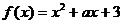 的最值。
的最值。
解:由已知有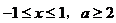 ,于是函数
,于是函数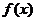 是定义在区间
是定义在区间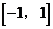 上的二次函数,将
上的二次函数,将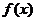 配方得:
配方得:
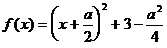
二次函数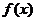 的对称轴方程是
的对称轴方程是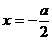
顶点坐标为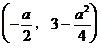 ,图象开口向上
,图象开口向上
由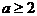 可得
可得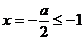 ,显然其顶点横坐标在区间
,显然其顶点横坐标在区间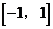 的左侧或左端点上。
的左侧或左端点上。
函数的最小值是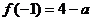 ,最大值是
,最大值是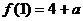 。
。
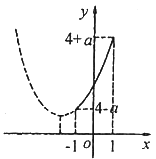
图3
例4. 已知二次函数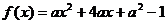 在区间
在区间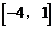 上的最大值为5,求实数a的值。
上的最大值为5,求实数a的值。
解:将二次函数配方得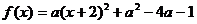 ,其对称轴方程为
,其对称轴方程为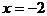 ,顶点坐标为
,顶点坐标为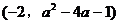 ,图象开口方向由a决定。很明显,其顶点横坐标在区间
,图象开口方向由a决定。很明显,其顶点横坐标在区间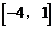 上。
上。
若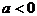 ,函数图象开口向下,如图4所示,当
,函数图象开口向下,如图4所示,当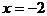 时,函数取得最大值5
时,函数取得最大值5
即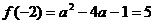
解得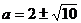
故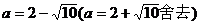
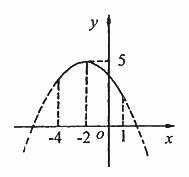
图4
若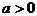 时,函数图象开口向上,如图5所示,当
时,函数图象开口向上,如图5所示,当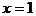 时,函数取得最大值5
时,函数取得最大值5
即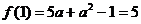
解得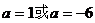
故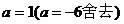
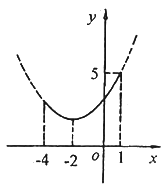
图5
综上讨论,函数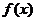 在区间
在区间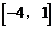 上取得最大值5时,
上取得最大值5时,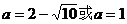
解后反思:例3中,二次函数的对称轴是随参数a变化的,但图象开口方向是固定的;例4中,二次函数的对称轴是固定的,但图象开口方向是随参数a变化的。
二次函数是给定的,给出的定义域区间也是固定的,我们称这种情况是“定二次函数在定区间上的最值”。
例1. 函数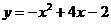 在区间
在区间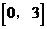 上的最大值是_________,最小值是_______。
上的最大值是_________,最小值是_______。
解:函数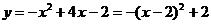 是定义在区间
是定义在区间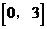 上的二次函数,其对称轴方程是
上的二次函数,其对称轴方程是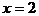 ,顶点坐标为(2,2),且其图象开口向下,显然其顶点横坐标在[0,3]上,如图1所示。函数的最大值为
,顶点坐标为(2,2),且其图象开口向下,显然其顶点横坐标在[0,3]上,如图1所示。函数的最大值为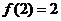 ,最小值为
,最小值为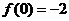 。
。
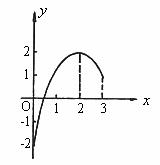
图1
例2. 已知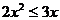 ,求函数
,求函数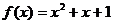 的最值。
的最值。
解:由已知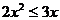 ,可得
,可得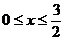 ,即函数
,即函数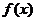 是定义在区间
是定义在区间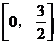 上的二次函数。将二次函数配方得
上的二次函数。将二次函数配方得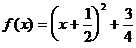 ,其对称轴方程
,其对称轴方程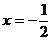 ,顶点坐标
,顶点坐标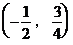 ,且图象开口向上。显然其顶点横坐标不在区间
,且图象开口向上。显然其顶点横坐标不在区间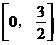 内,如图2所示。函数
内,如图2所示。函数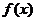 的最小值为
的最小值为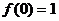 ,最大值为
,最大值为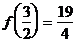 。
。
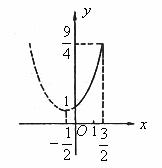
图2
解后反思:已知二次函数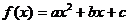 (不妨设
(不妨设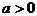 ),它的图象是顶点为
),它的图象是顶点为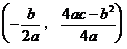 、对称轴为
、对称轴为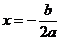 、开口向上的抛物线。由数形结合可得在
、开口向上的抛物线。由数形结合可得在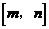 上
上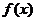 的最大值或最小值:
的最大值或最小值:
(1)当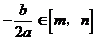 时,
时,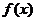 的最小值是
的最小值是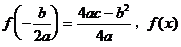 的最大值是
的最大值是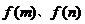 中的较大者。
中的较大者。
(2)当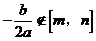 时
时
若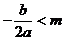 ,由
,由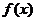 在
在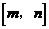 上是增函数
上是增函数
则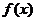 的最小值是
的最小值是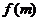 ,最大值是
,最大值是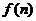
若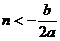 ,由
,由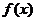 在
在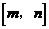 上是减函数
上是减函数
则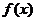 的最大值是
的最大值是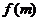 ,最小值是
,最小值是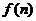
有些数学问题具有一定的迷惑性,如果概念不清,见识不广,就容易混淆,错误地将不同问题混为一谈了。所以通过反思形相似,但质不同的题目,能够提高辨别能力,避免错解的发生,这是一种总结性的反思。
例5. 对不等式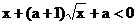 ,分别求满足下列条件的实数a的取值范围;
,分别求满足下列条件的实数a的取值范围;
(1)不等式的解集为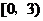 ;
;
(2)不等式在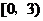 上有解;
上有解;
(3)不等式在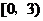 上恒成立;
上恒成立;
(4)不等式的解集是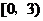 的子集。
的子集。
分析:由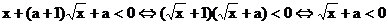
当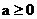 时,
时,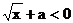 无解,原不等式解集为空集;当
无解,原不等式解集为空集;当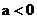 时,原不等式解集为(0,
时,原不等式解集为(0,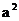 )
)
则(1)必须且只须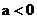 时,
时,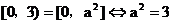 且
且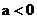 ,故
,故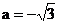 ;
;
(2)必须且只须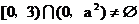 ,则
,则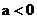 时均适合,即
时均适合,即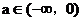 ;
;
(3)必须且只须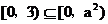 ,且
,且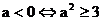 且
且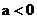 ,则
,则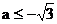 ,即
,即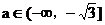 ;
;
(4)应有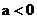 时,
时,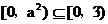 ,此时
,此时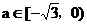 或为空集(
或为空集(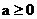 时),故
时),故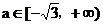
注:上述四个小题常容易混淆,通过反思各种解决方法的不同,弄清了四个不同的概念及相应的解题方案。
总之,解题后注重反思能培养良好的思维品质,既可促进“双基”的掌握,又能加强知识的有效迁移,是提高解题能力的重要途径。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
解题后反思,思什么? |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
解题后反思,思什么? |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
许咏梅 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
某些看似十分复杂的运算,经过巧妙转换,恒等变形,使运算对象发生转移,起到意想不到的效果。
例7. 求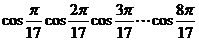 的值。
的值。
解:设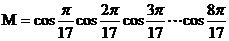
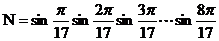
则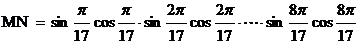
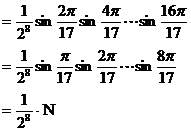
而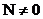 ,故
,故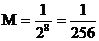
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
解题中的“设而不求”综述 |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
解题中的“设而不求”综述 |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
许咏梅 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
根据解题需要,可引入一个中间量作为中介,起到过渡作用,使问题得以解决。
例6. 如图3,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥体积分成相等的两部分,求圆锥母线与轴的夹角α。
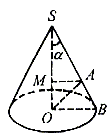
图3
解:过点A作SO的垂线,垂足为M,可知
∠MAO=∠AOB=∠OSB=α
设MA=x,OB=r,SO=h
则有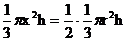
化简可得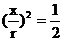
又因为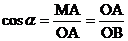
即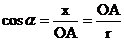
所以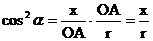
于是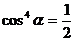 ,从而
,从而
解题过程中,不断变换观察角度,类比方法、联想内容,明确最终目标,经过巧妙构造,活用性质,可直达目标。
例5. 求证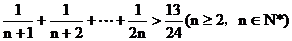
证明:设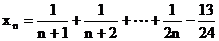
则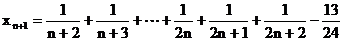
由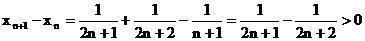 可知:数列
可知:数列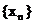 为单调递增数列。
为单调递增数列。
又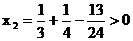
则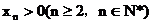
即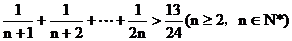
在解析几何问题中,对于有关点的坐标采用设而不求的策略,能促使问题定向,简便化归,起到以简驭繁的解题效果。
例4. 设抛物线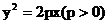 的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC//x轴,求证:直线AC经过原点O。
的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC//x轴,求证:直线AC经过原点O。
证明:设点A(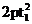 ,
,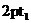 )、B(
)、B(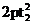 ,
,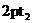 ),则点C(
),则点C(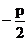 ,
,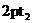 )
)
因为AB过焦点F
所以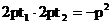
得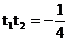
又直线OC的斜率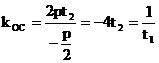
直线OA的斜率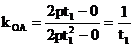 ,则
,则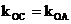
故A、O、C三点共线,即直线AC经过原点O。
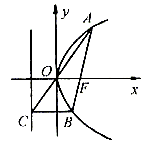
图2
恰当合理地引入参数,可使解题目标更加明确,已知和欲求之间的联系得以明朗化,使问题能够得到解决。
例3. 已知对任何满足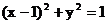 的实数x、y,如果
的实数x、y,如果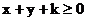 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
解:设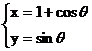 (
(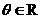 ),则
),则
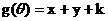
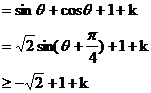
令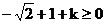 ,得
,得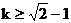
有些代数问题,通过挖掘题目中隐含的几何背景,设而不求,可转化成几何问题求解。
例2. 设a、b均为正数,且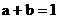 ,求证
,求证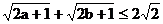 。
。
证明:设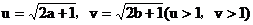 ,
,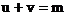
则u、v同时满足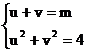
其中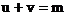 表示直线,m为此直线在v轴上的截距
表示直线,m为此直线在v轴上的截距
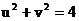 是以原点为圆心,2为半径的圆在第一象限内的一部分圆弧(如图1),显然直线与圆弧相切时,所对应的截距m的值最大。
是以原点为圆心,2为半径的圆在第一象限内的一部分圆弧(如图1),显然直线与圆弧相切时,所对应的截距m的值最大。
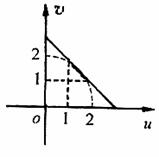
图1
由图易得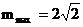
即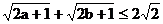
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com