
1.创设情景
复习:1.连续函数的概念;
1.5.2汽车行驶的路程
一:教学目标
知识与技能目标
了解求曲边梯形面积的过程和解决有关汽车行驶路程问题的过程的共同点;感受在其过程中渗透的思想方法:分割、以不变代变、求和、取极限(逼近)
过程与方法
通过与求曲边梯形的面积进行类比,求汽车行驶的路程有关问题,再一次体会“以直代曲“的思想
情感态度与价值观
在体会微积分思想的过程中,体会人类智慧的力量,培养世界是可知的等唯物主义的世界观
二:教学重难点
重点 掌握过程步骤:分割、以不变代变、求和、逼近(取极限)
难点 过程的理解
三:教学过程:
2.最后所得曲边形的面积不是近似值,而是真实值
例2.求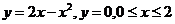 围成图形面积
围成图形面积
解:1.分割
在区间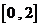 上等间隔地插入
上等间隔地插入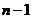 个点,将区间
个点,将区间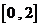 等分成
等分成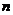 个小区间:
个小区间:
 ,
,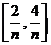 ,…,
,…,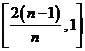
记第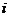 个区间为
个区间为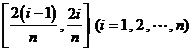 ,其长度为
,其长度为
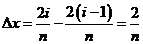
分别过上述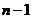 个分点作
个分点作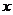 轴的垂线,从而得到
轴的垂线,从而得到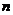 个小曲边梯形,他们的面积分别记作:
个小曲边梯形,他们的面积分别记作:
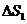 ,
,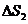 ,…,
,…,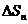
显然,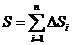
(2)近似代替
∵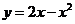 ,当
,当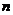 很大,即
很大,即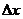 很小时,在区间
很小时,在区间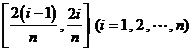 上,可以认为函数
上,可以认为函数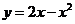 的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点
的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点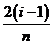 处的函数值
处的函数值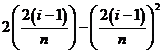 ,这样,在区间
,这样,在区间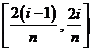 上,用小矩形的面积
上,用小矩形的面积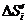 近似的代替
近似的代替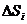 ,即在局部范围内“以直代取”,则有
,即在局部范围内“以直代取”,则有
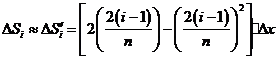
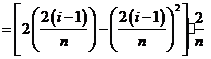 ①
①
(3)求和
由①,上图中阴影部分的面积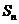 为
为
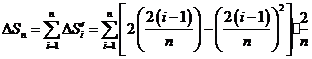
=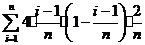 =
=
=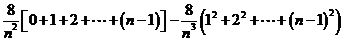
=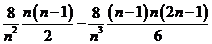
从而得到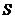 的近似值
的近似值 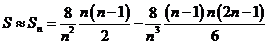
(4)取极限
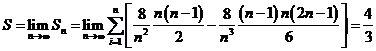
练习
设S表示由曲线 ,x=1,以及x轴所围成平面图形的面积。
,x=1,以及x轴所围成平面图形的面积。
四:课堂小结
求曲边梯形的思想和步骤:分割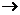 以直代曲
以直代曲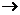 求和
求和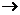 逼近 (“以直代曲”的思想)
逼近 (“以直代曲”的思想)
五:教学后记
3.求曲边梯形面积的四个步骤:
第一步:分割.在区间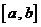 中任意插入
中任意插入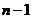 各分点,将它们等分成
各分点,将它们等分成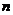 个小区间
个小区间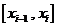
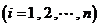 ,区间
,区间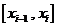 的长度
的长度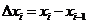 ,
,
第二步:近似代替,“以直代取”。用矩形的面积近似代替小曲边梯形的面积,求出每个小曲边梯形面积的近似值.
第三步:求和.
第四步:取极限。
说明:1.归纳以上步骤,其流程图表示为:
分割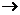 以直代曲
以直代曲 求和
求和 逼近
逼近
2.新课讲授
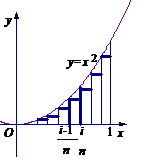
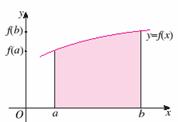 问题:如图,阴影部分类似于一个梯形,但有一边是曲线
问题:如图,阴影部分类似于一个梯形,但有一边是曲线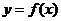 的一段,我们把由直线
的一段,我们把由直线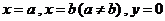 和曲线
和曲线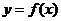 所围成的图形称为曲边梯形.如何计算这个曲边梯形的面积?
所围成的图形称为曲边梯形.如何计算这个曲边梯形的面积?
例1:求图中阴影部分是由抛物线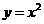 ,直线
,直线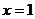 以及
以及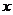 轴所围成的平面图形的面积S。
轴所围成的平面图形的面积S。
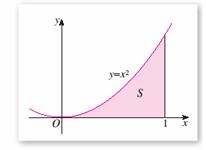
思考:(1)曲边梯形与“直边图形”的区别?
(2)能否将求这个曲边梯形面积S的问题转化为求“直边图形”面积的问题?
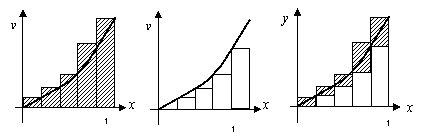 分析:曲边梯形与“直边图形”的主要区别:曲边梯形有一边是曲线段,“直边图形”的所有边都是直线段.“以直代曲”的思想的应用.
分析:曲边梯形与“直边图形”的主要区别:曲边梯形有一边是曲线段,“直边图形”的所有边都是直线段.“以直代曲”的思想的应用.
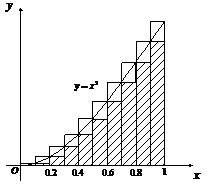
把区间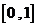 分成许多个小区间,进而把区边梯形拆为一些小曲边梯形,对每个小曲边梯形“以直代取”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值.分割越细,面积的近似值就越精确。当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S.也即:用划归为计算矩形面积和逼近的思想方法求出曲边梯形的面积.
分成许多个小区间,进而把区边梯形拆为一些小曲边梯形,对每个小曲边梯形“以直代取”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值,对这些近似值求和,就得到曲边梯形面积的近似值.分割越细,面积的近似值就越精确。当分割无限变细时,这个近似值就无限逼近所求曲边梯形的面积S.也即:用划归为计算矩形面积和逼近的思想方法求出曲边梯形的面积.
解:
(1).分割
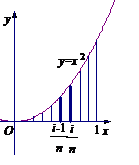 在区间
在区间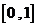 上等间隔地插入
上等间隔地插入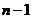 个点,将区间
个点,将区间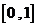 等分成
等分成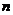 个小区间:
个小区间:
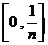 ,
,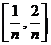 ,…,
,…,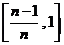
记第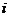 个区间为
个区间为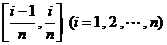 ,其长度为
,其长度为
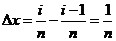
 分别过上述
分别过上述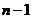 个分点作
个分点作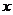 轴的垂线,从而得到
轴的垂线,从而得到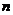 个小曲边梯形,他们的面积分别记作:
个小曲边梯形,他们的面积分别记作:
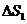 ,
,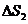 ,…,
,…,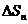
显然,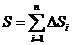
(2)近似代替
记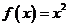 ,如图所示,当
,如图所示,当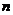 很大,即
很大,即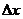 很小时,在区间
很小时,在区间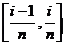 上,可以认为函数
上,可以认为函数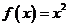 的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点
的值变化很小,近似的等于一个常数,不妨认为它近似的等于左端点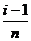 处的函数值
处的函数值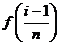 ,从图形上看,就是用平行于
,从图形上看,就是用平行于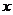 轴的直线段近似的代替小曲边梯形的曲边(如图).这样,在区间
轴的直线段近似的代替小曲边梯形的曲边(如图).这样,在区间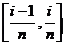 上,用小矩形的面积
上,用小矩形的面积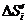 近似的代替
近似的代替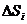 ,即在局部范围内“以直代取”,则有
,即在局部范围内“以直代取”,则有
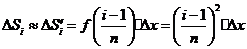
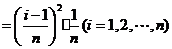 ①
①
(3)求和
由①,上图中阴影部分的面积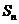 为
为
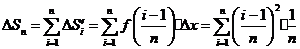
=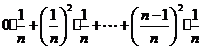 =
=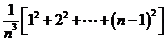
=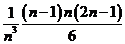 =
=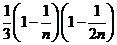
从而得到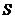 的近似值
的近似值 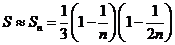
(4)取极限
分别将区间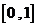 等分8,16,20,…等份(如图),可以看到,当
等分8,16,20,…等份(如图),可以看到,当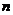 趋向于无穷大时,即
趋向于无穷大时,即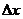 趋向于0时,
趋向于0时,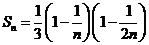 趋向于
趋向于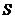 ,从而有
,从而有
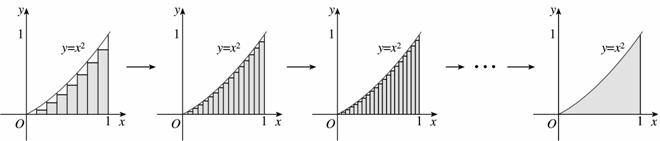
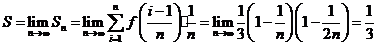
从数值上的变化趋势:
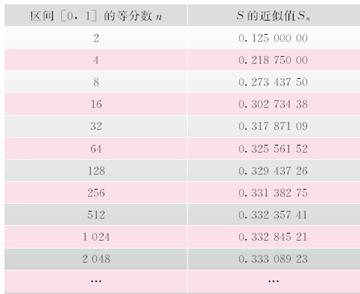

1.创设情景
我们学过如何求正方形、长方形、三角形等的面积,这些图形都是由直线段围成的。那么,如何求曲线围成的平面图形的面积呢?
这就是定积分要解决的问题。
定积分在科学研究和实际生活中都有非常广泛的应用。本节我们将学习定积分的基本概念以及定积分的简单应用,初步体会定积分的思想及其应用价值。
一个概念:如果函数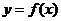 在某一区间
在某一区间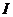 上的图像是一条连续不断的曲线,那么就把函数
上的图像是一条连续不断的曲线,那么就把函数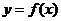 称为区间
称为区间 上的连续函数.(不加说明,下面研究的都是连续函数)
上的连续函数.(不加说明,下面研究的都是连续函数)
1.5.1曲边梯形的面积
一:教学目标
知识与技能目标
理解求曲边图形面积的过程:分割、以直代曲、逼近,感受在其过程中渗透的思想方法
过程与方法
情感态度与价值观
二:教学重难点
重点 掌握过程步骤:分割、以直代曲、求和、逼近(取极限)
难点 对过程中所包含的基本的微积分 “以直代曲”的思想的理解
三:教学过程:
|
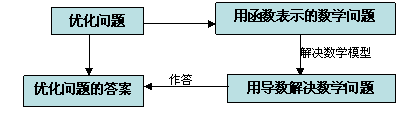

2.解决优化问题的方法:通过搜集大量的统计数据,建立与其相应的数学模型,再通过研究相应函数的性质,提出优化方案,使问题得到解决.在这个过程中,导数往往是一个有利的工具。
5.课本 练习
1.用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.(高为1.2 m,最大容积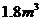 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com