
1.求下列函数的极值.
(1)y=x2-7x+6 (2)y=x3-27x
(1)解:y′=(x2-7x+6)′=2x-7
令y′=0,解得x=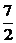 .
.
当x变化时,y′,y的变化情况如下表.
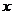 |
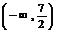 |
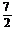 |
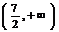 |
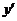 |
- |
0 |
+ |
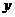 |
↘ |
极小值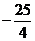 |
↗ |
∴当x=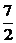 时,y有极小值,且y极小值=-
时,y有极小值,且y极小值=-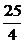 .
.
(2)解:y′=(x3-27x)′=3x2-27=3(x+3)(x-3)
令y′=0,解得x1=-3,x2=3.
当x变化时,y′,y的变化情况如下表.
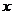 |
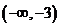 |
-3 |
(-3,3) |
3 |
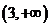 |
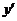 |
+ |
0 |
- |
0 |
+ |
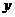 |
↗ |
极大值54 |
↘ |
极小值-54 |
↗ |
∴当x=-3时,y有极大值,且y极大值=54.
当x=3时,y有极小值,且y极小值=-54
5. 求可导函数f(x)的极值的步骤:
(1)确定函数的定义区间,求导数f′(x) 
(2)求方程f′(x)=0的根
(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号即都为正或都为负,那么f(x)在这个根处无极值

如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点 
4. 判别f(x0)是极大、极小值的方法:
若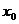 满足
满足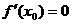 ,且在
,且在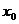 的两侧
的两侧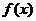 的导数异号,则
的导数异号,则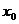 是
是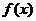 的极值点,
的极值点,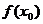 是极值,并且如果
是极值,并且如果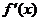 在
在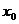 两侧满足“左正右负”,则
两侧满足“左正右负”,则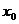 是
是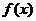 的极大值点,
的极大值点,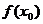 是极大值;如果
是极大值;如果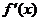 在
在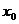 两侧满足“左负右正”,则
两侧满足“左负右正”,则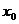 是
是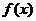 的极小值点,
的极小值点,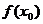 是极小值
是极小值
3.极大值与极小值统称为极值 注意以下几点:
注意以下几点:
(ⅰ)极值是一个局部概念 由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小
由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小 并不意味着它在函数的整个的定义域内最大或最小
并不意味着它在函数的整个的定义域内最大或最小
(ⅱ)函数的极值不是唯一的 即一个函数在某区间上或定义域内极大值或极小值可以不止一个
即一个函数在某区间上或定义域内极大值或极小值可以不止一个
(ⅲ)极大值与极小值之间无确定的大小关系 即一个函数的极大值未必大于极小值,如下图所示,
即一个函数的极大值未必大于极小值,如下图所示,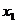 是极大值点,
是极大值点,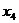 是极小值点,而
是极小值点,而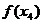 >
>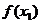

(ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点
而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点
2.极小值:一般地,设函数f(x)在x0附近有定义,如果对x0附近的所有的点,都有f(x)>f(x0).就说f(x0)是函数f(x)的一个极小值,记作y极小值=f(x0),x0是极小值点
例1.(课本例4)求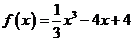 的极值
的极值
解: 因为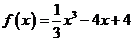 ,所以
,所以
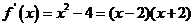 。
。
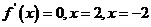
下面分两种情况讨论:
(1)当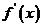 >0,即
>0,即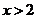 ,或
,或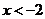 时;
时;
(2)当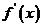 <0,即
<0,即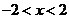 时.
时.
当x变化时,
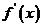 ,
,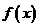 的变化情况如下表:
的变化情况如下表:
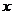 |
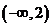 |
-2 |
(-2,2) |
2 |
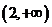 |
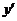 |
+ |
0 |
- |
0 |
+ |
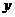 |
↗ |
极大值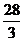 |
↘ |
极小值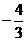 |
↗ |
因此,当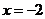 时,
时,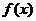 有极大值,并且极大值为
有极大值,并且极大值为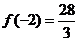 ;
;
当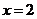 时,
时,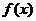 有极小值,并且极小值为
有极小值,并且极小值为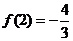 。
。
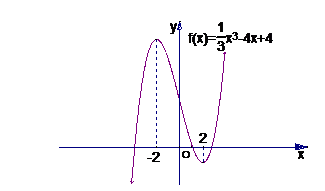
函数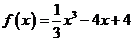 的图像如图所示。
的图像如图所示。
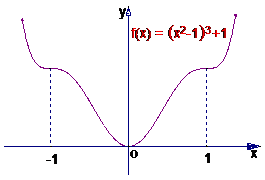
例2求y=(x2-1)3+1的极值
解:y′=6x(x2-1)2=6x(x+1)2(x-1)2
令y′=0解得x1=-1,x2=0,x3=1
当x变化时,y′,y的变化情况如下表
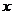 |
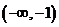 |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
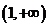 |
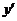 |
- |
0 |
- |
0 |
+ |
0 |
+ |
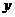 |
↘ |
无极值 |
↘ |
极小值0 |
↗ |
无极值 |
↗ |
∴当x=0时,y有极小值且y极小值=0
1.极大值:
一般地,设函数f(x)在点x0附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0),就说f(x0)是函数f(x)的一个极大值,记作y极大值=f(x0),x0是极大值点
3.求解函数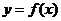 单调区间的步骤:
单调区间的步骤:
(1)确定函数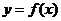 的定义域;
的定义域;
(2)求导数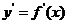 ;
;
(3)解不等式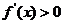 ,解集在定义域内的部分为增区间;
,解集在定义域内的部分为增区间;
(4)解不等式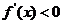 ,解集在定义域内的部分为减区间.
,解集在定义域内的部分为减区间.
2.函数的单调性与导数的关系
观察下面函数的图像,探讨函数的单调性与其导数正负的关系.
如图3.3-3,导数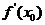 表示函数
表示函数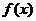 在点
在点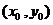 处的切线的斜率.在
处的切线的斜率.在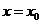 处,
处,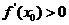 ,切线是“左下右上”式的,这时,函数
,切线是“左下右上”式的,这时,函数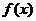 在
在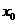 附近单调递增;在
附近单调递增;在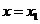 处,
处,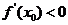 ,切线是“左上右下”式的,这时,函数
,切线是“左上右下”式的,这时,函数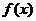 在
在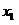 附近单调递减.
附近单调递减.
结论:函数的单调性与导数的关系
在某个区间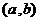 内,如果
内,如果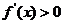 ,那么函数
,那么函数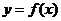 在这个区间内单调递增;如果
在这个区间内单调递增;如果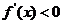 ,那么函数
,那么函数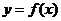 在这个区间内单调递减.
在这个区间内单调递减.
说明:(1)特别的,如果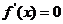 ,那么函数
,那么函数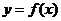 在这个区间内是常函数.
在这个区间内是常函数.
1.问题:图3.3-1(1),它表示跳水运动中高度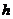 随时间
随时间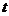 变化的函数
变化的函数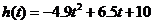 的图像,图3.3-1(2)表示高台跳水运动员的速度
的图像,图3.3-1(2)表示高台跳水运动员的速度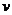 随时间
随时间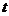 变化的函数
变化的函数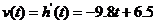 的图像.
的图像.
运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
通过观察图像,我们可以发现:
(1)
运动员从起点到最高点,离水面的高度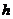 随时间
随时间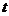 的增加而增加,即
的增加而增加,即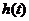 是增函数.相应地,
是增函数.相应地,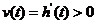 .
.
(2)
从最高点到入水,运动员离水面的高度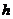 随时间
随时间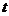 的增加而减少,即
的增加而减少,即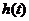 是减函数.相应地,
是减函数.相应地,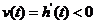 .
.
观察图3.3-8,我们发现,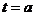 时,高台跳水运动员距水面高度最大.那么,函数
时,高台跳水运动员距水面高度最大.那么,函数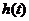 在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?
在此点的导数是多少呢?此点附近的图像有什么特点?相应地,导数的符号有什么变化规律?
放大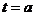 附近函数
附近函数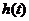 的图像,如图3.3-9.可以看出
的图像,如图3.3-9.可以看出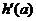 ;在
;在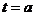 ,当
,当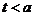 时,函数
时,函数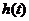 单调递增,
单调递增,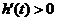 ;当
;当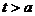 时,函数
时,函数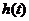 单调递减,
单调递减,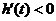 ;这就说明,在
;这就说明,在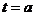 附近,函数值先增(
附近,函数值先增(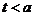 ,
,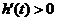 )后减(
)后减(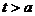 ,
,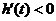 ).这样,当
).这样,当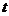 在
在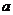 的附近从小到大经过
的附近从小到大经过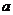 时,
时,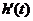 先正后负,且
先正后负,且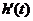 连续变化,于是有
连续变化,于是有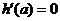 .
.

对于一般的函数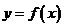 ,是否也有这样的性质呢?
,是否也有这样的性质呢?
附:对极大、极小值概念的理解,可以结合图象进行说明.并且要说明函数的极值是就函数在某一点附近的小区间而言的. 从图象观察得出,判别极大、极小值的方法.判断极值点的关键是这点两侧的导数异号
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com