
3.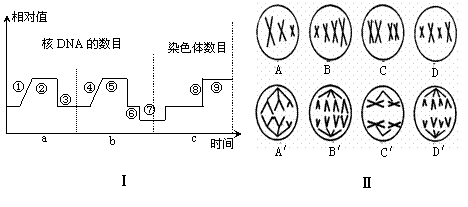 图Ⅰ表示细胞分裂和受精过程中核DNA和染色体含量的变化,图Ⅱ表示二倍体生物细胞分裂过程中染色体的行为。据图分析,下列说法正确的是
图Ⅰ表示细胞分裂和受精过程中核DNA和染色体含量的变化,图Ⅱ表示二倍体生物细胞分裂过程中染色体的行为。据图分析,下列说法正确的是
A.Ⅰ中染色体数目加倍发生在①、④、⑧和⑨4个时期
B.Ⅰ中只有③、⑥、⑦和⑨时期的染色体数目与DNA数目相等
C.Ⅱ中与Ⅰa对应的细胞是B和B',与Ⅰb段对应的是C和 C'
D.Ⅱ中含有两个染色体组的细胞有A'、B'、C、C'、D
2.关于细胞结构和功能的说法正确的是
A.颤藻和衣藻都能通过叶绿体的光合作用合成有机物
B.癌细胞中糖蛋白和核糖体的数量明显少于衰老细胞
C.Na+进入神经元的方式与神经元释放递质的方式不同
D.所有细胞中核糖体的形成都与核仁密切相关
1.下表是某同学为验证酶的专一性而设计的实验方案,a-d代表试管,①-⑦代表实验步骤。对该实验方案的有关评价,错误的是
|
|
a |
b |
c |
d |
|
① |
淀粉溶液 2ml |
蔗糖溶液 2ml |
唾液淀粉酶溶液2ml |
唾液淀粉 酶溶液2ml |
|
② |
50-65℃温水中水浴加热10min |
|||
|
③ |
将c倒入a,将d倒入b |
|||
|
④ |
50-65℃温水中水浴加热10min |
|||
|
⑤ |
加入现配的斐林试剂溶液2ml |
|||
|
⑥ |
37℃恒温水浴 |
|||
|
⑦ |
观察并记录颜色变化 |
A.淀粉酶的用量属于自变量 B.②和④会影响酶的活性
C.②﹑④和⑥的温度设置错误 D.④和⑤的顺序有误
(1)求变速直线运动的路程
我们知道,作变速直线运动的物体所经过的路程s,等于其速度函数v=v (t) ( v(t) ≥0) 在时间区间[a,b]上的定积分,即

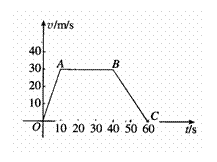 例 4。一辆汽车的速度一时间曲线如图1.7 一3 所示.求汽车在这1 min 行驶的路程.
例 4。一辆汽车的速度一时间曲线如图1.7 一3 所示.求汽车在这1 min 行驶的路程.
解:由速度一时间曲线可知:

因此汽车在这 1 min 行驶的路程是:
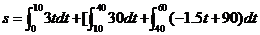
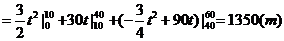
答:汽车在这 1 min 行驶的路程是 1350m .
2.变力作功
一物体在恒力F(单位:N)的作用下做直线运动,如果物体沿着与F相同的方向移(单位:m),则力F所作的功为W=Fs .
探究
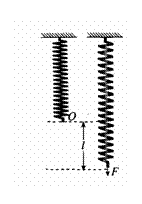 如果物体在变力 F(x)的作用下做直线运动,并且物体沿着与 F (x) 相同的方向从x =a 移动到x=b (a<b) ,那么如何计算变力F(x)所作的功W呢?
如果物体在变力 F(x)的作用下做直线运动,并且物体沿着与 F (x) 相同的方向从x =a 移动到x=b (a<b) ,那么如何计算变力F(x)所作的功W呢?
与求曲边梯形的面积和求变速直线运动的路程一样,可以用“四步曲”解决变力作功问题.可以得到

例5.如图1·7一4 ,在弹性限度内,将一弹簧从平衡位置拉到离平衡位置lm 处,求克服弹力所作的功.
解:在弹性限度内,拉伸(或压缩)弹簧所需的力 F ( x )与弹簧拉伸(或压缩)的长度 x 成正比,即 F ( x )= kx ,
其中常数 k 是比例系数.
由变力作功公式,得到
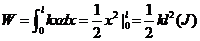
答:克服弹力所作的功为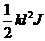 .
.
例6.A、B两站相距7.2km,一辆电车从A站B开往站,电车开出ts后到达途中C点,这一段的速度为1.2t(m/s),到C点的速度为24m/s,从C点到B点前的D点以等速行驶,从D点开始刹车,经ts后,速度为(24-1.2t)m/s,在B点恰好停车,试求
(1)A、C间的距离;(2)B、D间的距离;(3)电车从A站到B站所需的时间。
分析:作变速直线运动的物体所经过的路程s,等于其速度函数v=v(t)(v(t)≥0)在时间区间[a,b]上的定积分,即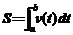
略解:(1)设A到C的时间为t1则1.2t=24,
t1=20(s),则AC=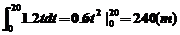
(2)设D到B的时间为t21则24-1.2t2=0, t21=20(s),
则DB=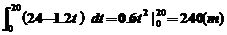
(3)CD=7200-2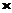 240=6720(m),则从C到D的时间为280(s),则所求时间为20+280+20=320(s)
240=6720(m),则从C到D的时间为280(s),则所求时间为20+280+20=320(s)
例3:如果1N能拉长弹簧1cm,为了将弹簧拉长6cm,需做功( A )
A 0.18J B 0.26J C 0.12J D 0.28J
略解:设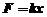 ,则由题可得
,则由题可得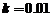 ,所以做功就是求定积分
,所以做功就是求定积分 。
。
练习:
四:课堂小结
本节课主要学习了利用定积分求一些曲边图形的面积与体积,即定积分在几何中应用,以及定积分在物理学中的应用,要掌握几种常见图形面积的求法,并且要注意定积分的几何意义,不能等同于图形的面积,要注意微积分的基本思想的应用与理解。
五教后反思
根据定积分的定义,定积分既有几何背景,又有物理背景,进而定积分与这些知识有着天然的联系。譬如:求几何图形的面积,求路程、平均速度、电荷量、电压、功、质量等。上述种种尽管形式相异,然而所采用的思想方法均是:化曲为直,以不变代变,逼近,从某个角度而言充分展现了数学思想方法的高度抽象性及应用的广泛性
3.求旋转体的体积和侧面积
由曲线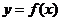 ,直线
,直线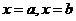 及
及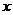 轴所围成的曲边梯形绕
轴所围成的曲边梯形绕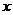 轴旋转而成的旋转体体积为
轴旋转而成的旋转体体积为
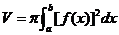 .
.
其侧面积为
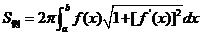 .
.
2.求平面曲线的弧长
设曲线AB方程为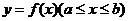 ,函数
,函数 在区间
在区间 上可导,且
上可导,且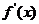 连续,则曲线AB的弧长为
连续,则曲线AB的弧长为
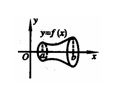
 .
.
3、几种常见的曲边梯形面积的计算方法:
(1)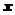 型区域:
型区域:
①由一条曲线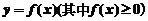 与直线
与直线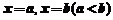 以及
以及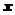 轴所围成的曲边梯形的面积:
轴所围成的曲边梯形的面积: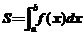 (如图(1));
(如图(1));
②由一条曲线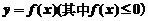 与直线
与直线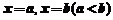 以及
以及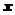 轴所围成的曲边梯形的面积:
轴所围成的曲边梯形的面积: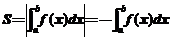 (如图(2));
(如图(2));
③由两条曲线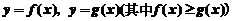 与直线
与直线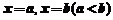

图(1) 图(2) 图(3)
所围成的曲边梯形的面积: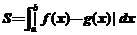 (如图(3));
(如图(3));
(2)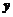 型区域:
型区域:
①由一条曲线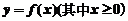 与直线
与直线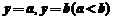 以及
以及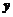 轴所围成的曲边梯形的面积,可由
轴所围成的曲边梯形的面积,可由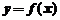 得
得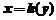 ,然后利用
,然后利用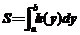 求出(如图(4));
求出(如图(4));
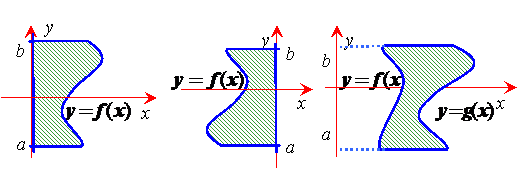
②由一条曲线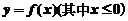 与直线
与直线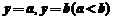 以及
以及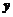 轴所围成的曲边梯形的面积,可由
轴所围成的曲边梯形的面积,可由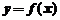 先求出
先求出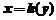 ,然后利用
,然后利用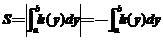 求出(如图(5));
求出(如图(5));
 ③由两条曲线
③由两条曲线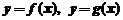 与直线
与直线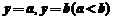 所围成的曲边梯形的面积,可由
所围成的曲边梯形的面积,可由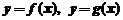 先分别求出
先分别求出 ,
,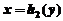 ,然后利用
,然后利用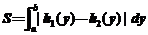 求出(如图(6));
求出(如图(6));
图(4) 图(5) 图(6)
2、求曲边梯形面积的方法与步骤:
(1) 画图,并将图形分割为若干个曲边梯形;
(2) 对每个曲边梯形确定其存在的范围,从而确定积分的上、下限;
(3) 确定被积函数;
(4) 求出各曲边梯形的面积和,即各积分的绝对值的和。
4、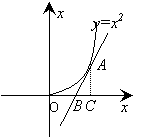 在曲线
在曲线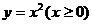 上的某点A处作一切线使之与曲线以及
上的某点A处作一切线使之与曲线以及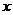 轴所围成的面积为
轴所围成的面积为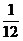 .试求:切点A的坐标以及切线方程.
.试求:切点A的坐标以及切线方程.
略解:如图由题可设切点坐标为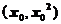 ,则切线方程
,则切线方程
为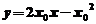 ,切线与
,切线与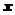 轴的交点坐标为
轴的交点坐标为
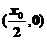 ,则由题可知有
,则由题可知有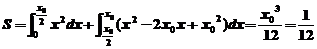
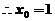 ,所以切点坐标与切线方程分别为
,所以切点坐标与切线方程分别为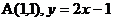
总结:1、定积分的几何意义是: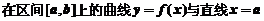 、
、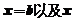 轴所围成的图形的面积的代数和,即
轴所围成的图形的面积的代数和,即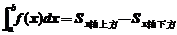 .
.
因此求一些曲边图形的面积要可以利用定积分的几何意义以及微积分基本定理,但要特别注意图形面积与定积分不一定相等,如函数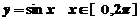 的图像与
的图像与 轴围成的图形的面积为4,而其定积分为0.
轴围成的图形的面积为4,而其定积分为0.
3、求曲线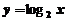 与曲线
与曲线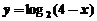 以及
以及 轴所围成的图形面积。
轴所围成的图形面积。
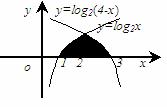 略解:所求图形的面积为
略解:所求图形的面积为
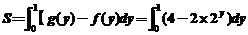
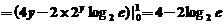
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com