
6.能熟练掌握由tanα的值(m)求sinα、cosα的值的方法:若α是锐角,就根据tanα的值画一个直角三角形,在该直角三角形中求sinα、cosα;若α不一定是锐角,则由方程组:sinα=mcosα, sin2α+cos2α=1解得,或“弦化切”。在三角变换中,要注意1的功用。“弦化切”时常把1化为正弦与余弦的平方;在三角变换中常用两倍角余弦公式消去1,如: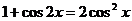 ,
,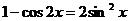 ,,
,,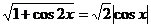 ,
,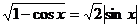 等,此外
等,此外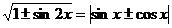 .
.
[举例]已知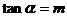 ,其中
,其中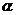 为第二象限角,求(1)
为第二象限角,求(1)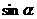 ,
,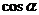 的值;
的值;
(2)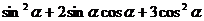 的值;
的值;
解析:(1)将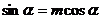 代入
代入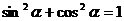 得:(
得:(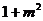 )
)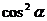 =1
=1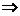
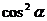 =
=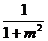 ,又
,又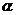 为第二象限角,∴
为第二象限角,∴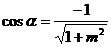 ,
, =
=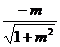
(2)原式=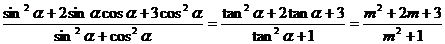 。
。
(分子、分母同除以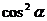 是“弦化切”的基本动作)
是“弦化切”的基本动作)
[巩固]已知2sin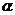 -cos
-cos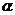 =1求sin
=1求sin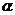 +2cos
+2cos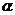 的值。
的值。
[迁移] 设向量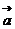 =(1+cosα,sinα),
=(1+cosα,sinα),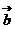 =(1-cosβ,sinβ),
=(1-cosβ,sinβ),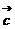 =(1,0),α∈(0,
=(1,0),α∈(0, ),β∈(
),β∈( ,2
,2 ),
),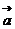 与
与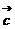 的夹角为θ1,
的夹角为θ1,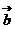 与
与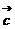 的夹角为θ2,且θ1―θ2=
的夹角为θ2,且θ1―θ2=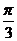 ,求
,求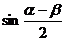 的值。
的值。
5. 三角变换中遇到形如: sinα±cosα=m的条件,如果是研究性质的问题,常“合二为一”;如果是求值的问题,常两边平方,得到sinαcosα的值并判断出sinα、cosα的符号,再与sinα±cosα=m联立,解方程组。sinα±cosα与sinαcosα“三兄妹”关系密切,要做到见此及彼;其中sinαcosα=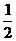 [(sinα+cosα)2-1]=
[(sinα+cosα)2-1]= 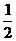 [1-(sinα-cosα)2],
[1-(sinα-cosα)2],
sinα+cosα与sinα-cosα通过sinαcosα实现过渡.
[举例] 已知a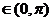 ,若
,若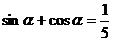 ,求
,求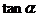 的值。
的值。
解析:思路一:联立方程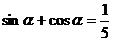 ①和
①和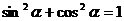 ②,
②,
解得: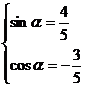 或
或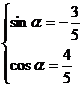 ∵a
∵a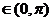 ∴
∴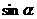 >0,后一组接舍去,∴
>0,后一组接舍去,∴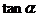 =-
=-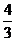 。
。
思路二:由①平方得: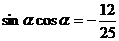 ③,联立①③运用韦达定理求得两组
③,联立①③运用韦达定理求得两组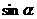 和
和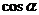 的值,舍去一组后得出
的值,舍去一组后得出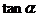 的值。思路三:利用③容易求得
的值。思路三:利用③容易求得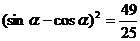 ,注意到
,注意到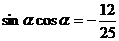 <0即
<0即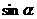 和
和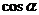 异号,∵a
异号,∵a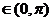 ∴
∴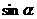 >0,
>0, 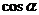 <0;
<0;
∴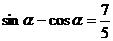 ④;联立①④得到
④;联立①④得到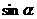 和
和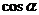 的值,再求出
的值,再求出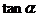 的值。
的值。
思路四:由①平方得: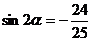 <0,∵a
<0,∵a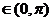 ∴
∴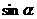 >0,
>0, 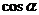 <0,∴a
<0,∴a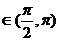 ; 又
; 又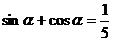 >0,
∴
>0,
∴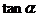 <-1,∴a
<-1,∴a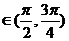 ,∴
,∴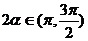 ,∴
,∴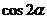 =
=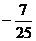 再用半角公式求出
再用半角公式求出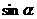 和
和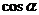 的值。
的值。
[巩固]若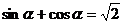 ,则
,则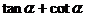 等于 ( )
等于 ( )
A. 1 B. 2 C. –1 D. –2
[迁移1]设θ是三角形的一个内角,且Sinθ+Cosθ=,则方程x2Sinθ+y2Cosθ=1表示的曲线是(A)焦点在x轴上的椭圆 (B焦点在y轴上的椭圆 ( )
(C)焦点在x轴上的双曲线 (D)焦点在y轴上的双曲线
[迁移2]函数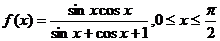 的值域为
的值域为
4.求具体角的三角函数值的一般方法:角负化正、大化小。必须熟记常用几个特殊角的三角函数值,很多“疏忽”皆源于此;而在“无条件”求值问题中,恰倒好处地运用特殊角三角函数值又往往是解题的关键。
[举例]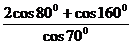 的值是: ( )
的值是: ( )
A.-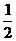 B.-
B.-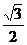 C.
-
C.
-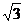 D. -
D. -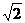
解析:用两倍角公式,很快就会发现进行不下去。尝试“大化小”,原式=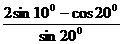 =
=
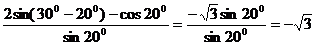 ,选C。(把100换成300-200是关键)。
,选C。(把100换成300-200是关键)。
[巩固1]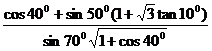 =
=
[巩固2] 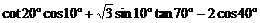 =
=
[迁移] 若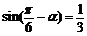 ,则
,则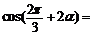
(A)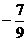 (B)
(B)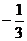 (C)
(C)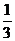 (D)
(D)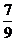
3. 熟悉将三角函数式化为y=Asin(ωx+φ)+B的套路。即:运用两倍角正(余)弦公式及半角公式降次、(其中sin2x=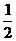 (1-cos2x),cos2x=
(1-cos2x),cos2x=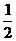 (1+cos2x)这两个公式使用频繁,必须牢记)再引入辅助角(特别注意
(1+cos2x)这两个公式使用频繁,必须牢记)再引入辅助角(特别注意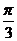 ,
,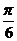 经常弄错)使用两角和、差的正弦、余弦公式(合二为一)。这是三角变换中最常用的一套“组合拳”,要能娴熟而精准地使用。
经常弄错)使用两角和、差的正弦、余弦公式(合二为一)。这是三角变换中最常用的一套“组合拳”,要能娴熟而精准地使用。
[举例]函数f(x)=6sinxcosx-8sin2x取得最大值时tan2x的值为 。
解析:f(x)=3sin2x-4(1-cos2x)=3sin2x+4cos2x-4=5(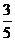 sin2x+
sin2x+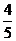 cos2x)-4=5sin(2x+
cos2x)-4=5sin(2x+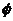 )-4
)-4
(其中tan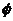 =
=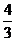 ),当且仅当2x+
),当且仅当2x+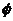 =2k
=2k +
+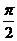 即2x=2k
即2x=2k +
+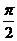 -
-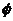 , k∈Z时函数f(x) 取得最大值,此时tan2x=tan(2k
, k∈Z时函数f(x) 取得最大值,此时tan2x=tan(2k +
+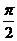 -
-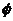 )=cot
)=cot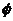 =
=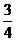 。注意:上述过程中“5(
。注意:上述过程中“5(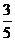 sin2x+
sin2x+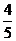 cos2x)-4”这一步最好不要跳过,它是保证辅助角
cos2x)-4”这一步最好不要跳过,它是保证辅助角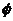 不出错的最重要的关口。
不出错的最重要的关口。
[巩固] 函数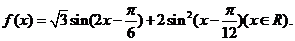 的最大值为
的最大值为
2.已知一个角的某一三角函数值求角的大小,一定要根据角的范围来确定;如: sin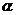 =m(|m|<1),则
=m(|m|<1),则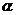 =2k
=2k +arcsinm或
+arcsinm或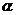 =2k
=2k +
+ -arcsinm;cos
-arcsinm;cos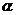 =m(|m|<1),则
=m(|m|<1),则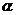 =2k
=2k ±arccosm; tan
±arccosm; tan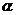 =m,则
=m,则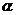 =k
=k +arctanm, k∈Z等。两个角的三角函数值相等,这两个角未必相等,如sinα=sinβ, 则α=2k
+arctanm, k∈Z等。两个角的三角函数值相等,这两个角未必相等,如sinα=sinβ, 则α=2k +β, 或α=2k
+β, 或α=2k +
+ -β,k
-β,k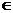 Z; 若cosα=cosβ, 则α=2k
Z; 若cosα=cosβ, 则α=2k
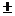 β;
若tanα=tanβ, 则α=k
β;
若tanα=tanβ, 则α=k +β,k
+β,k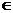 Z 等。
Z 等。
[举例1]已知sin2A=sin2B,则⊿ABC的形状为__________
解析:∵ sin2A=sin2B 且2A+2B∈(0,2 ),∴2A=2B或2A+2B=
),∴2A=2B或2A+2B=
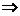
A=B或A+B=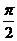 即⊿ABC是等腰或直角三角形。
即⊿ABC是等腰或直角三角形。
[举例2]已知sin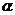 =-
=-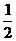 ,
,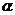 ∈(-
∈(-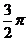 ,-
,-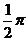 ),求
),求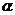
解析:sin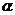 =-
=-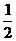 ,则
,则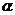 =2k
=2k -
-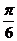 或
或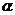 =2k
=2k
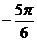 , k∈Z,又
, k∈Z,又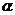 ∈(-
∈(-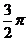 ,-
,-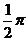 )
)
∴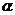 =
=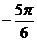 。
。
[巩固] 如果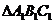 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于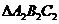 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A.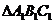 和
和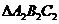 都是锐角三角形 B.
都是锐角三角形 B.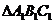 和
和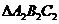 都是钝角三角形
都是钝角三角形
C.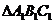 是钝角三角形,
是钝角三角形,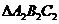 是锐角三角形
是锐角三角形
D.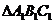 是锐角三角形,
是锐角三角形,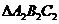 是钝角三角形
是钝角三角形
[提高]已知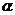 ∈(0,
∈(0,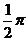 ),则直线x+ytan
),则直线x+ytan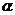 +1=0的倾角
+1=0的倾角
A.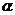 B.
B.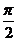 -
-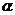 C.
C.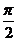 +
+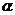 D.
D. -
-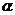
1.若α∈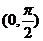 ,则sinα< α<tanα;角的终边“靠近”Y轴时,正弦、正切绝对值较大,角的终边“靠近”X轴时,余弦、余切绝对值较大 。
,则sinα< α<tanα;角的终边“靠近”Y轴时,正弦、正切绝对值较大,角的终边“靠近”X轴时,余弦、余切绝对值较大 。
[举例1]若x ∈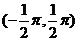 ,求方程sinx=tanx解的个数。
,求方程sinx=tanx解的个数。
解析:在图象中要能体现出(0,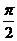 )上sinα<tanα,注意:横纵坐标的长度单位要一致
)上sinα<tanα,注意:横纵坐标的长度单位要一致
(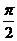 >1),(图象略)1个。
>1),(图象略)1个。
[举例2]已知q是第二象限的角,且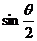 <
<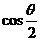 ,那么
,那么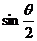 +
+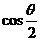 的取值范围是
的取值范围是
A (-1、0) B (1、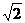 )
C (-1、1)
D (-
)
C (-1、1)
D (-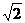 、-1)
、-1)
解析:q是第二象限的角,则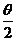 ∈(k
∈(k +
+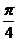 ,k
,k +
+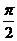 )k∈Z,(一、三象限中“靠近”y轴的部分),∵
)k∈Z,(一、三象限中“靠近”y轴的部分),∵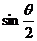 <
<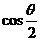 ,∴
,∴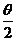 不在第一象限(第一象限正、余弦均为正,“靠近”y轴正弦较大),即
不在第一象限(第一象限正、余弦均为正,“靠近”y轴正弦较大),即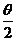 ∈(2 k
∈(2 k +
+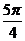 ,2 k
,2 k +
+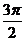 )k∈Z,
)k∈Z,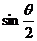 +
+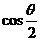 =
=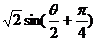 ,
,
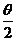 +
+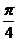 ∈(2 k
∈(2 k +
+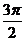 ,2 k
,2 k +
+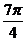 ),由图象知:
),由图象知: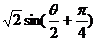 ∈(-
∈(-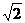 、-1),选D。
、-1),选D。
[巩固1]若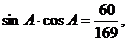 且
且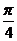 <
<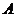 <
<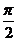 ,则
,则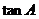 的值为 ( )
的值为 ( )
A.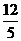 或
或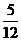 B.
B.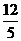 C.
C.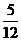 D.
D.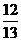
[巩固2]⊿ABC的内角A满足:且tanA-sinA<0,sinA+cosA>0,则A的取值范围是___
本题为选做题,考生须从所给(一)(二)两题中任选一题作答,不能全选。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com