5．课本　 练习

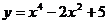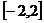4．求函数在区间上的最大值与最小值．

3．函数y=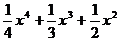，在［－1，1］上的最小值为(　　 )

A.0　　　　 　　 B.－2　 　C.－1　 　　　　 D.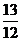

2．函数y=f(x)在区间［a,b］上的最大值是M，最小值是m,若M=m,则f′(x) (　 )

A.等于0　　　　　　　 B.大于0　　 C.小于0　　　　　　　　 D.以上都有可能

1．下列说法正确的是(　　 )

A.函数的极大值就是函数的最大值 B.函数的极小值就是函数的最小值

C.函数的最值一定是极值　　　　 D.在闭区间上的连续函数一定存在最值

例1．(课本例5)求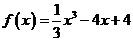在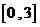的最大值与最小值　

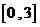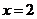解： 由例4可知，在上，当时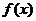，有极小值，并且极小值为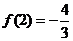，又由于，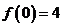

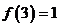
因此，函数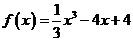在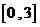的最大值是4，最小值是．

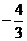上述结论可以从函数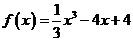在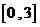上的图象得到直观验证．

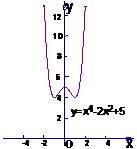
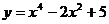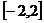例2．求函数在区间上的最大值与最小值

解：先求导数，得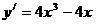

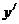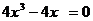令＝0即解得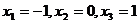

导数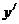的正负以及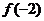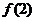，如下表

从上表知，当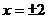时，函数有最大值13，当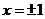时，函数有最小值4

例3．已知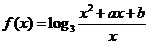,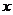∈(0,+∞).是否存在实数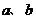,使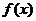同时满足下列两个条件：(1)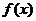)在(0，1)上是减函数，在［1，+∞)上是增函数；(2)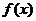的最小值是1，若存在，求出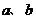，若不存在，说明理由.

解：设g(x)=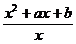

∵f(x)在(0，1)上是减函数，在［1，+∞)上是增函数

∴g(x)在(0，1)上是减函数，在［1，+∞)上是增函数.

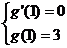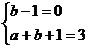∴　　 ∴　 解得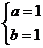

经检验，a=1,b=1时，f(x)满足题设的两个条件.

3．利用导数求函数的最值步骤:

由上面函数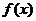的图象可以看出，只要把连续函数所有的极值与定义区间端点的函数值进行比较，就可以得出函数的最值了．

一般地，求函数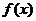在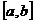上的最大值与最小值的步骤如下：

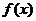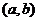⑴求在内的极值；

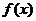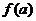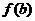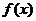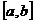⑵将的各极值与端点处的函数值、比较，其中最大的一个是最大值，最小的一个是最小值，得出函数在上的最值

2．“最值”与“极值”的区别和联系

⑴最值”是整体概念，是比较整个定义域内的函数值得出的，具有绝对性；而“极值”是个局部概念，是比较极值点附近函数值得出的，具有相对性．

⑵从个数上看，一个函数在其定义域上的最值是唯一的；而极值不唯一；

⑶函数在其定义区间上的最大值、最小值最多各有一个，而函数的极值可能不止一个，也可能没有一个

⑷极值只能在定义域内部取得，而最值可以在区间的端点处取得，有极值的未必有最值，有最值的未必有极值；极值有可能成为最值，最值只要不在端点必定是极值．

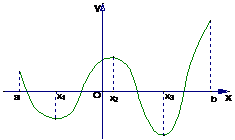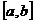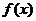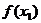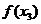观察图中一个定义在闭区间上的函数的图象．图中与是极小值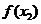，是极大值．函数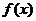在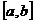上的最大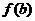值是，最小值是．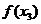

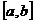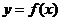1．结论：一般地，在闭区间上函数的图像是一条连续不断的曲线，那么函数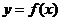在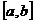上必有最大值与最小值．

说明：⑴如果在某一区间上函数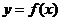的图像是一条连续不断的曲线，则称函数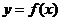在这个区间上连续．(可以不给学生讲)

⑵给定函数的区间必须是闭区间，在开区间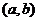内连续的函数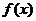不一定有最大值与最小值．如函数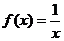在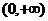内连续，但没有最大值与最小值；

⑶在闭区间上的每一点必须连续，即函数图像没有间断，

⑷函数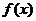在闭区间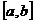上连续，是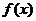在闭区间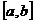上有最大值与最小值的充分条件而非必要条件．(可以不给学生讲)

我们知道，极值反映的是函数在某一点附近的局部性质，而不是函数在整个定义域内的性质．也就是说，如果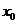是函数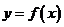的极大(小)值点，那么在点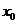附近找不到比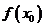更大(小)的值．但是，在解决实际问题或研究函数的性质时，我们更关心函数在某个区间上，哪个至最大，哪个值最小．如果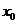是函数的最大(小)值，那么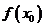不小(大)于函数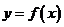在相应区间上的所有函数值．