2．定积分的几何意义　

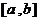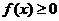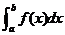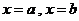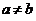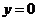如果在区间上函数连续且恒有，那么定积分表示由直线()，和曲线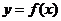所围成的曲边梯形的面积。

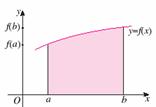
说明：一般情况下，定积分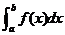的几何意义是介于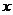轴、函数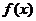的图形以及直线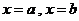之间各部分面积的代数和，在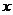轴上方的面积取正号，在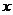轴下方的面积去负号．

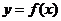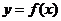分析：一般的，设被积函数，若在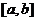上可取负值。

考察和式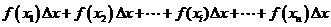

不妨设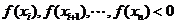

于是和式即为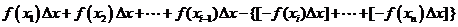

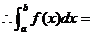阴影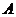的面积-阴影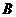的面积(即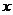轴上方面积减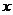轴下方的面积)

1．定积分的概念 一般地，设函数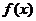在区间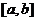上连续，用分点

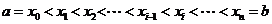
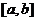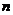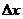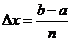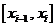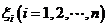将区间等分成个小区间，每个小区间长度为()，在每个小区间上取一点，作和式：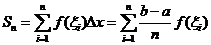

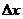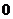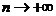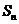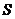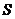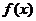如果无限接近于(亦即)时，上述和式无限趋近于常数，那么称该常数为函数在区间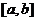上的定积分。记为：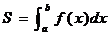　　　

其中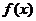成为被积函数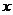，叫做积分变量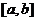，为积分区间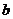，积分上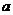限，积分下限。

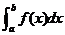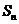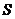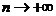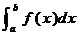说明：(1)定积分是一个常数，即无限趋近的常数(时)称为，而不是．

　　 (2)用定义求定积分的一般方法是：

①分割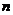：等分区间；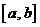

②近似代替：取点；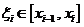

③求和：；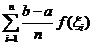

④取极限：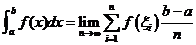

(3)曲边图形面积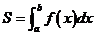：；变速运动路程；

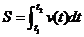变力做功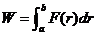

2．新课讲授

2．对这四个步骤再以分析、理解、归纳，找出共同点．

1． 回忆前面曲边图形面积，变速运动的路程，变力做功等问题的解决方法，解决步骤：分割→以直代曲→求和→取极限(逼近　　　

1．创设情景

复习：

1.5.3定积分的概念

一：教学目标　

知识与技能目标　

通过求曲边梯形的面积和变速直线运动的路程，了解定积分的背景；

能用定积分的定义求简单的定积分；

理解掌握定积分的几何意义；

过程与方法

借助于几何直观定积分的基本思想，理解定积分的概念；

情感态度与价值观

二：教学重难点　

重点　 定积分的概念、定积分法求简单的定积分、定积分的几何意义

难点　定积分的概念、定积分的几何意义

三：教学目标：

1．分割

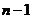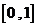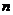在区间上等间隔地插入个点，将区间等分成个小区间：

　　　　　　 ，，…，　

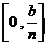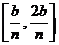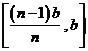
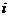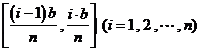记第个区间为，其长度为

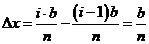
把在分段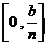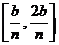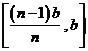，，…，上所作的功分别记作：

　　　　　 ，，…，

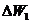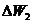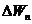
(2)近似代替

有条件知：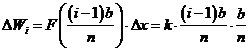　

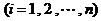
(3)求和

=

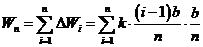
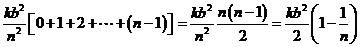
从而得到的近似值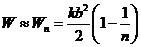

(4)取极限

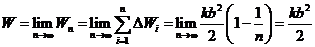
所以得到弹簧从平衡位置拉长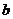所作的功为：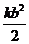

四：课堂小结

求汽车行驶的路程有关问题的过程．

五：教学后记

2．新课讲授

问题：汽车以速度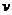组匀速直线运动时，经过时间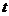所行驶的路程为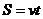．如果汽车作变速直线运动，在时刻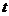的速度为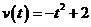(单位：km/h)，那么它在0≤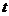≤1(单位：h)这段时间内行驶的路程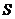(单位：km)是多少？

分析：与求曲边梯形面积类似，采取“以不变代变”的方法，把求匀变速直线运动的路程问题，化归为匀速直线运动的路程问题．把区间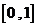分成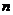个小区间，在每个小区间上，由于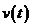的变化很小，可以近似的看作汽车作于速直线运动，从而求得汽车在每个小区间上行驶路程的近似值，在求和得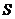(单位：km)的近似值，最后让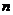趋紧于无穷大就得到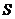(单位：km)的精确值．(思想：用化归为各个小区间上匀速直线运动路程和无限逼近的思想方法求出匀变速直线运动的路程)．

解：1．分割

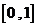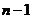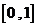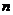在时间区间上等间隔地插入个点，将区间等分成个小区间：

　　　　　　 ，，…，　

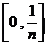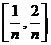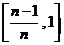
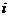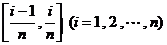记第个区间为，其长度为

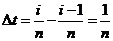
把汽车在时间段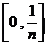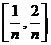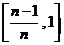，，…，上行驶的路程分别记作：

　　　　　 ，，…，

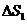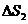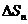
显然，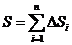

(2)近似代替

当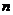很大，即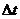很小时，在区间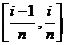上，可以认为函数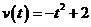的值变化很小，近似的等于一个常数，不妨认为它近似的等于左端点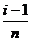处的函数值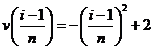，从物理意义上看，即使汽车在时间段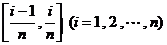上的速度变化很小，不妨认为它近似地以时刻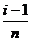处的速度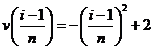作匀速直线运动，即在局部小范围内“以匀速代变速”，于是的用小矩形的面积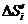近似的代替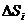，即在局部范围内“以直代取”，则有

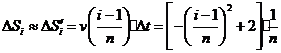
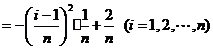　①

(3)求和

由①，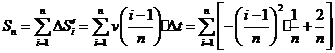

==

==

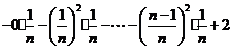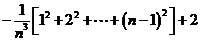
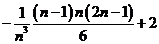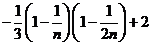
从而得到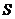的近似值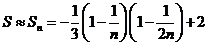

(4)取极限

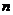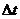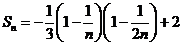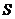当趋向于无穷大时，即趋向于0时，趋向于，从而有

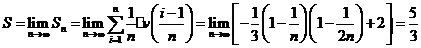
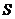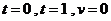思考：结合求曲边梯形面积的过程，你认为汽车行驶的路程与由直线和曲线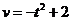所围成的曲边梯形的面积有什么关系？

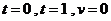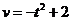结合上述求解过程可知，汽车行驶的路程在数据上等于由直线和曲线所围成的曲边梯形的面积．

一般地，如果物体做变速直线运动，速度函数为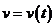，那么我们也可以采用分割、近似代替、求和、取极限的方法，利用“以不变代变”的方法及无限逼近的思想，求出它在a≤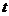≤b内所作的位移．

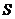例1．弹簧在拉伸的过程中，力与伸长量成正比，即力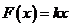(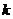为常数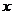，是伸长量)，求弹簧从平衡位置拉长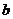所作的功．

分析：利用“以不变代变”的思想，采用分割、近似代替、求和、取极限的方法求解．

解： 将物体用常力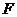沿力的方向移动距离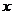，则所作的功为．

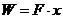2．求曲边梯形面积的基本思想和步骤；

利用导数我们解决了“已知物体运动路程与时间的关系，求物体运动速度”的问题．反之，如果已知物体的速度与时间的关系，如何求其在一定时间内经过的路程呢？