
(1)函数的单调性与导数的关系
(2)求解函数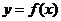 单调区间
单调区间
(3)证明可导函数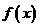 在
在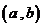 内的单调性
内的单调性
2.课本 练习
1.f(x)=2x3-6x2+7
2.f(x)=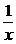 +2x
3. f(x)=sinx , x
+2x
3. f(x)=sinx , x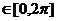 4. y=xlnx
4. y=xlnx
1.求下列函数的单调区间
例1.已知导函数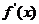 的下列信息:
的下列信息:
当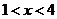 时,
时,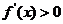 ;
;
当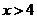 ,或
,或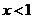 时,
时,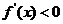 ;
;
当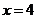 ,或
,或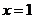 时,
时,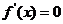
试画出函数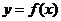 图像的大致形状.
图像的大致形状.
解:当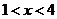 时,
时,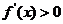 ,可知
,可知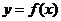 在此区间内单调递增;
在此区间内单调递增;
当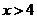 ,或
,或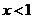 时,
时,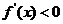 ;可知
;可知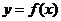 在此区间内单调递减;
在此区间内单调递减;
当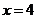 ,或
,或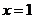 时,
时,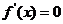 ,这两点比较特殊,我们把它称为“临界点”.
,这两点比较特殊,我们把它称为“临界点”.
综上,函数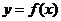 图像的大致形状如图3.3-4所示.
图像的大致形状如图3.3-4所示.
例2.判断下列函数的单调性,并求出单调区间.
(1)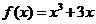 ;
(2)
;
(2)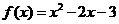
(3)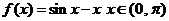 ; (4)
; (4)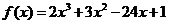
解:(1)因为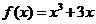 ,所以,
,所以,
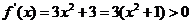
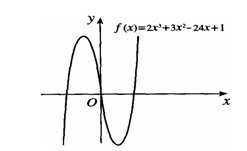
因此,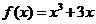 在R上单调递增,如图3.3-5(1)所示.
在R上单调递增,如图3.3-5(1)所示.
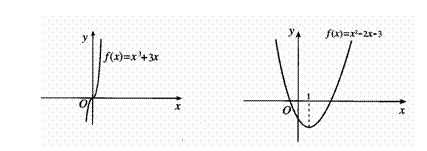
(2)因为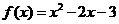 ,所以,
,所以, 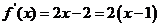
当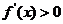 ,即
,即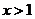 时,函数
时,函数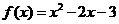 单调递增;
单调递增;
当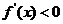 ,即
,即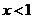 时,函数
时,函数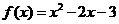 单调递减;
单调递减;
函数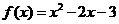 的图像如图3.3-5(2)所示.
的图像如图3.3-5(2)所示.
(3)因为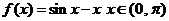 ,所以,
,所以,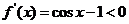
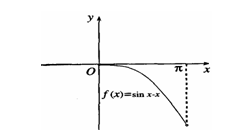
因此,函数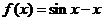 在
在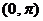 单调递减,如图3.3-5(3)所示.
单调递减,如图3.3-5(3)所示.
(4)因为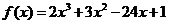 ,所以
.
,所以
.
当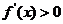 ,即
时,函数
,即
时,函数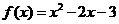 ;
;
当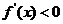 ,即
时,函数
,即
时,函数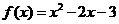 ;
;
函数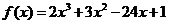 的图像如图3.3-5(4)所示.
的图像如图3.3-5(4)所示.
注:(3)、(4)生练
例3.如图3.3-6,水以常速(即单位时间内注入水的体积相同)注入下面四种底面积相同的容器中,请分别找出与各容器对应的水的高度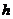 与时间
与时间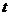 的函数关系图像.
的函数关系图像.
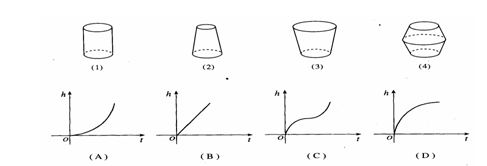
分析:以容器(2)为例,由于容器上细下粗,所以水以常速注入时,开始阶段高度增加得慢,以后高度增加得越来越快.反映在图像上,(A)符合上述变化情况.同理可知其它三种容器的情况.
解: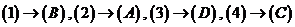
思考:例3表明,通过函数图像,不仅可以看出函数的增减,还可以看出其变化的快慢.结合图像,你能从导数的角度解释变化快慢的情况吗?
一般的,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化的快,这时,函数的图像就比较“陡峭”;反之,函数的图像就“平缓”一些.
如图3.3-7所示,函数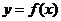 在
在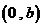 或
或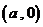 内的图像“陡峭”,
内的图像“陡峭”,
在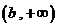 或
或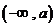 内的图像“平缓”.
内的图像“平缓”.
例4.求证:函数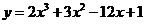 在区间
在区间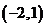 内是减函数.
内是减函数.
证明:因为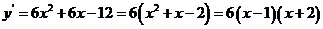
当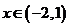 即
即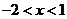 时,
时,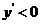 ,所以函数
,所以函数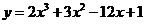 在区间
在区间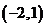 内是减函数.
内是减函数.
说明:证明可导函数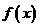 在
在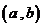 内的单调性步骤:
内的单调性步骤:
(1)求导函数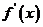 ;
;
(2)判断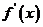 在
在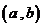 内的符号;
内的符号;
(3)做出结论: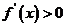 为增函数,
为增函数,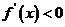 为减函数.
为减函数.
例5.已知函数 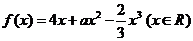 在区间
在区间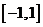 上是增函数,求实数
上是增函数,求实数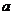 的取值范围.
的取值范围.
解: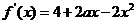 ,因为
,因为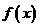 在区间
在区间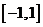 上是增函数,所以
上是增函数,所以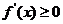 对
对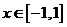 恒成立,即
恒成立,即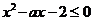 对
对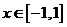 恒成立,解之得:
恒成立,解之得: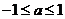
所以实数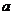 的取值范围为
的取值范围为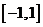 .
.
说明:已知函数的单调性求参数的取值范围是一种常见的题型,常利用导数与函数单调性关系:即“若函数单调递增,则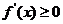 ;若函数单调递减,则
;若函数单调递减,则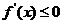 ”来求解,注意此时公式中的等号不能省略,否则漏解.
”来求解,注意此时公式中的等号不能省略,否则漏解.
例6.已知函数y=x+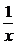 ,试讨论出此函数的单调区间.
,试讨论出此函数的单调区间.
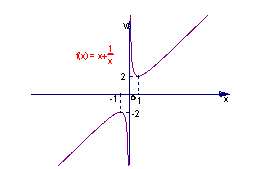 解:y′=(x+
解:y′=(x+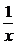 )′
)′
=1-1·x-2=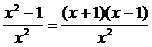
令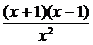 >0.
>0.
解得x>1或x<-1.
∴y=x+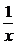 的单调增区间是(-∞,-1)和(1,+∞).
的单调增区间是(-∞,-1)和(1,+∞).
令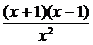 <0,解得-1<x<0或0<x<1.
<0,解得-1<x<0或0<x<1.
∴y=x+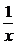 的单调减区间是(-1,0)和(0,1)
的单调减区间是(-1,0)和(0,1)
3.求解函数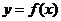 单调区间的步骤:
单调区间的步骤:
(1)确定函数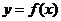 的定义域;
的定义域;
(2)求导数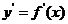 ;
;
(3)解不等式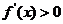 ,解集在定义域内的部分为增区间;
,解集在定义域内的部分为增区间;
(4)解不等式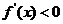 ,解集在定义域内的部分为减区间.
,解集在定义域内的部分为减区间.
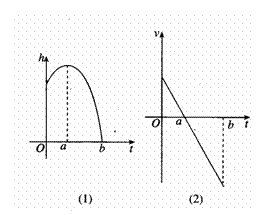 1.问题:图3.3-1(1),它表示跳水运动中高度
1.问题:图3.3-1(1),它表示跳水运动中高度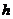 随时间
随时间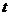 变化的函数
变化的函数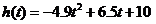 的图像,图3.3-1(2)表示高台跳水运动员的速度
的图像,图3.3-1(2)表示高台跳水运动员的速度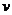 随时间
随时间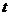 变化的函数
变化的函数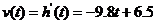 的图像.
的图像.
运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?
通过观察图像,我们可以发现:
(1)
运动员从起点到最高点,离水面的高度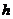 随时间
随时间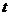 的增加而增加,即
的增加而增加,即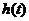 是增函数.相应地,
是增函数.相应地,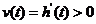 .
.
(2)
从最高点到入水,运动员离水面的高度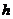 随时间
随时间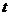 的增加而减少,即
的增加而减少,即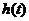 是减函数.相应地,
是减函数.相应地,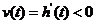 .
.
2.函数的单调性与导数的关系
观察下面函数的图像,探讨函数的单调性与其导数正负的关系.
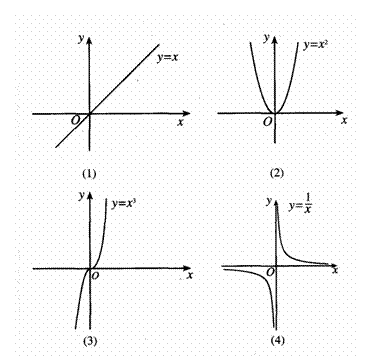
如图3.3-3,导数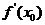 表示函数
表示函数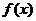 在点
在点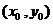 处的切线的斜率.
处的切线的斜率.
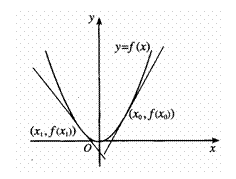
在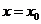 处,
处,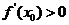 ,切线是“左下右上”式的,这时,函数
,切线是“左下右上”式的,这时,函数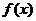 在
在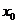 附近单调递增;
附近单调递增;
在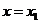 处,
处,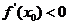 ,切线是“左上右下”式的,这时,函数
,切线是“左上右下”式的,这时,函数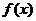 在
在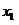 附近单调递减.
附近单调递减.
结论:函数的单调性与导数的关系
在某个区间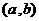 内,如果
内,如果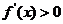 ,那么函数
,那么函数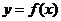 在这个区间内单调递增;如果
在这个区间内单调递增;如果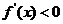 ,那么函数
,那么函数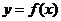 在这个区间内单调递减.
在这个区间内单调递减.
说明:(1)特别的,如果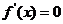 ,那么函数
,那么函数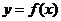 在这个区间内是常函数.
在这个区间内是常函数.
函数是客观描述世界变化规律的重要数学模型,研究函数时,了解函数的赠与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的.通过研究函数的这些性质,我们可以对数量的变化规律有一个基本的了解.下面,我们运用导数研究函数的性质,从中体会导数在研究函数中的作用.
2.求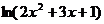 的导数
的导数
1.求下列函数的导数 (1) y =sinx3+sin33x;(2)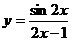 ;(3)
;(3)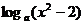
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com