
9、解:(1)
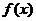 在(0,+
在(0,+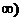 上为减函数。证明如下:
上为减函数。证明如下:
设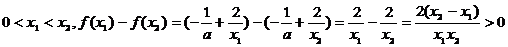
∴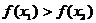 即
即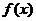 在(0,+
在(0,+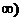 上为减函数。
上为减函数。
(2)不等式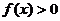 即
即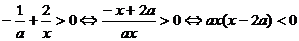
① 当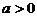 时 解集为
时 解集为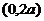 ②
当
②
当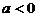 时解集为
时解集为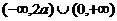
(3)若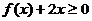 在(0,+
在(0,+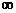 )上恒成立,即
)上恒成立,即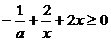
∴ 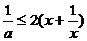 ∵
∵
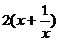 的最小值为4 ∴
的最小值为4 ∴ 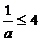
解得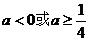
8、解:依题意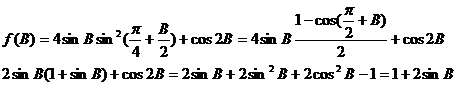 ,
,
由于对任意的三角形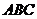 ,都有
,都有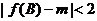 ,则:
,则: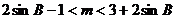 恒成立,则
恒成立,则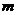 小于
小于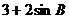 的最小值,大于
的最小值,大于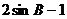 的最大值,则
的最大值,则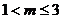 。
。
7、解: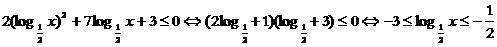
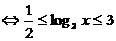
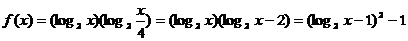
∵ 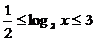 ∴当
∴当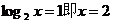 时
时 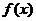 有最小值-1
有最小值-1
当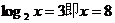 时
时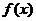 有最大值3
有最大值3
1、B 2、D 3、B 4、[-2,2] 5、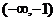 6、4
6、4
3、解:(1)、依题意,令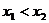 ,且
,且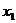 、
、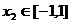 ,则
,则
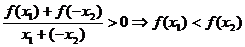 ,则函数
,则函数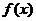 在
在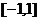 上的单调增。
上的单调增。
(2)、依题意,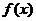 在
在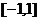 上的最大值为1,则
上的最大值为1,则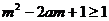 对
对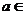
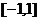 恒成立,
恒成立,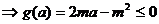 对
对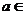
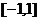 恒成立,
恒成立,
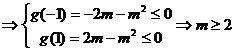 或
或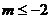 或
或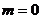 。
。
冲刺强化训练(5)
[强化训练]
2、解:命题P为真命题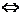 函数
函数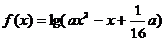 定义域为R
定义域为R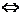
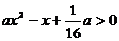 对任意实数
对任意实数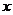 均成立
均成立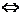
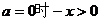 解集为R,或
解集为R,或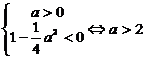 ∴ 命题P为真命题
∴ 命题P为真命题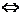
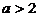
命题q为真命题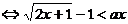 对一切正实数均成立
对一切正实数均成立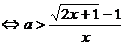
=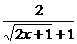 对一切正实数均成立。由于
对一切正实数均成立。由于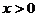 ∴
∴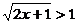 ∴
∴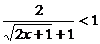
∴ 命题q为真命题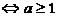
由已知命题p或q有且只有一个为真命题,当命题p为真命题且命题q为假命题时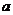 不存在;当命题p为假命题且命题q为真命题时
不存在;当命题p为假命题且命题q为真命题时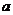 的范围为[1,2] 。∴
的范围为[1,2] 。∴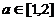
1、解:(1)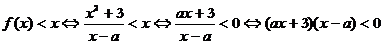
当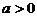 时,不等式解集为
时,不等式解集为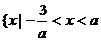 }
}
当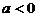 时,不等式解集为{
时,不等式解集为{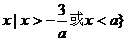
(2)设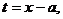 则
则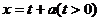
∴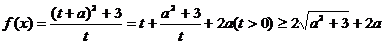
当且仅当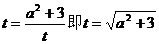 时,
时,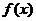 有最小值2
有最小值2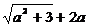
由题意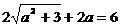 ,解得
,解得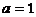
1、B 2、B 3、D
4、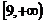 5、
5、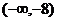
[例题探究]
9.已知函数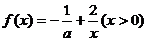
(1)
判断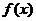 在(0,+
在(0,+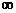 )上的增减性,并证明你的结论;
)上的增减性,并证明你的结论;
(2)
解关于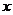 的不等式
的不等式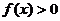 ;
;
(3)
若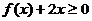 在(0,+
在(0,+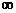 )上恒成立,求
)上恒成立,求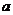 的范围。
的范围。
第5讲 不等式的应用
[课前热身]
8.在三角形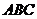 中,角
中,角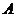 、
、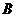 、
、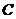 的对边的边长分别为
的对边的边长分别为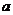 、
、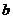 、
、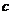 ,
,
已知: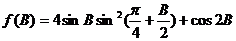 ,若对任意的三角形
,若对任意的三角形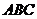 ,都有
,都有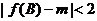 ,求实数
,求实数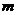 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com