
[例1]解关于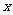 的不等式:
的不等式:
(1)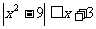 ; (2)
; (2)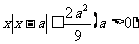
解:(1)法一:原不等式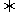
 ①或
①或
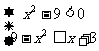 ②
②
由①解得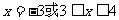 ,由②解得
,由②解得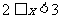
∴原不等式的解集是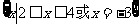
法二:原等式等价于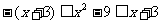

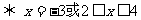
∴原不等式的解集是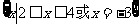
 法三:设
法三:设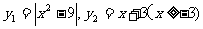 ,由
,由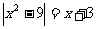 解得
解得
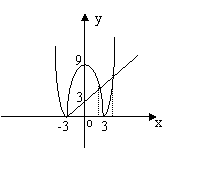
 ,在同一坐标系下作出它们的图象,由图得使
,在同一坐标系下作出它们的图象,由图得使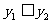 的
的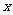 的范围是
的范围是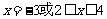 ,
,
∴原不等式的解集是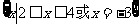
(2)当x≥a时,不等式可化为

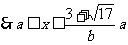
当x<a时,不等式可化为

 。
。
✿提炼方法:题(1)法2比较简单,其转化也不要求x+3>0.
题(2)的关键不是对参数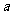 进行讨论,而是去绝对值时必须对未知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集。
进行讨论,而是去绝对值时必须对未知数进行讨论,得到两个不等式组,最后对两个不等式组的解集求并集,得出原不等式的解集。
[例2](1)已知a≠0,求证: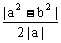 ≥
≥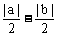
(2)求实数λ的取值范围,使不等式|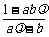 |>1对满足|a|<1,|b|<1的一切实数a、b恒成立;
|>1对满足|a|<1,|b|<1的一切实数a、b恒成立;
(3)已知|a|<1,若|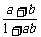 |<1,求b的取值范围.
|<1,求b的取值范围.
证明(1):当|a|≤|b|时,不等式显然成立
当|a|>|b|时,
左=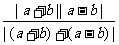 ≥
≥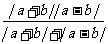
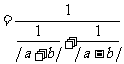 ≥
≥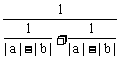 =
=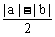 .
.
另法:当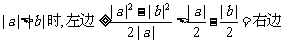
当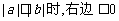 ,显然成立.
,显然成立.
(2)解:∵|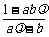 |>1
|>1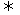 |1-abλ|2-|aλ-b|2
|1-abλ|2-|aλ-b|2
=(a2λ2-1)(b2-1)>0.
∵b2<1,∴a2λ2-1<0对于任意满足|a|<1的a恒成立.
当a=0时,a2λ2-1<0成立;
当a≠0时,要使λ2<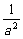 对于任意满足|a|<1的a恒成立,
对于任意满足|a|<1的a恒成立,
而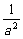 >1,∴|λ|≤1.故-1≤λ≤1.
>1,∴|λ|≤1.故-1≤λ≤1.
(3)|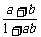 |<1
|<1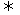 (
(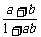 )2<1
)2<1
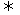 (a+b)2<(1+ab)2
(a+b)2<(1+ab)2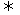 a2+b2-1-a2b2<0
a2+b2-1-a2b2<0
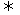 (a2-1)(b2-1)<0.
(a2-1)(b2-1)<0.
∵|a|<1,∴a2<1.∴1-b2>0,即-1<b<1.
[例3]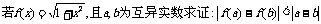
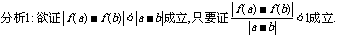


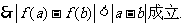
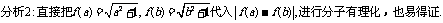

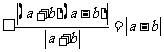
所以,原命题得证
[例4]设a,b∈R,关于x方程x2+ax+b=0的实根为α,β,若|a|+|b|<1,求证:
|α|<1,|β|<1。
解题思路分析:
在不等式、方程、函数的综合题中,通常以函数为中心。
法一:令f(x)=x2+ax+b
则 f(1)=1+a+b>1-(|a|+|b|)>1-1=0
f(-1)=1-a+b>1-(|a|+|b|)>0
又∵ 0 |a|≤|a|+|b|<1
|a|≤|a|+|b|<1
∴ -1<a<1 ∴ 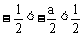
∴ f(x)=0的两根在(-1,1)内,即|α|<1,|β|<1
法二:∵α+β=-a,αβ=b
∴ |α+β|+|αβ|=|a|+|b|<1
∴ |α|-|β|+|α||β|<|α+β|+|αβ|<1
∴(|α|-1)(|β|+1)<0
∵ |β|+1>0 ∴ |α|<1. 同理:|β|<1
◆提炼方法:适度放缩是处理绝对值不等式的常用技巧,如|a|-|b|≤|a+b|及|b|-|a|≤|a±b|的选择等。
[研讨.欣赏] (2002 江苏)已知a>0,函数f(x)=ax-bx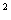 .
.
(1)当b>0时,若对任意x∈R都有f(x) 1,证明a
1,证明a 2
2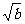 ;
;
(2)当b>1时,证明对任意x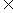 [0,1],都有|f(x)|
[0,1],都有|f(x)| 1的充要条件是b-1
1的充要条件是b-1 a
a 2
2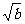 ;
;
(3)当0<b 1时,讨论:对任意x
1时,讨论:对任意x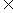 [0,1],都有|f(x)|
[0,1],都有|f(x)| 1的充要条件.
1的充要条件.
证明:⑴对已知二次函数应用配方法,得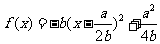 ,当x∈R时,f(x)
,当x∈R时,f(x)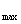 =
= 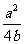 ,于是,对任意x∈R都有f(x)
,于是,对任意x∈R都有f(x) 1
1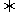 f(x)
f(x)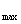 =
=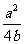
 1
1 a
a 2
2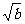 .
.
⑵用f(x)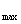 、f(x)
、f(x)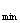 表示f(x)在[0,1]上的最大值、最小值,则对任意x∈[0,1],都有|f(x)|
表示f(x)在[0,1]上的最大值、最小值,则对任意x∈[0,1],都有|f(x)| 1当且仅当
1当且仅当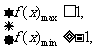 (*)
(*)
而
f(x)=-b(x-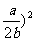 +
+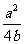 ,(x
,(x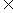 [0,1])
[0,1])
当2b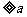 时,0<
时,0<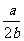
 1,f(x)
1,f(x)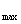 =
= 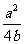 ,f(x)
,f(x)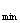 =f(0)或f(1);
=f(0)或f(1);
当2b<a时,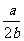 >1, f(x)
>1, f(x)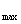 = f(1),f(x)
= f(1),f(x)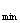 =f(0).
=f(0).
于是(*)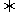
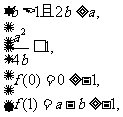 或
或
 b-1
b-1 a
a 2
2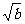 或x
或x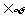
 b-1
b-1 a
a 2
2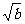 .
.
故对任意x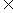 [0,1],都有|f(x)|
[0,1],都有|f(x)| 1的充要条件是b-1
1的充要条件是b-1 a
a 2
2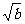 .
.
(3) 由(2)的解答知,对任意x∈[0,1],都有|f(x)| 1当且仅当
1当且仅当
 或
或
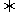 0<a
0<a 2b或2b<a
2b或2b<a b+1
b+1 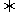 0<a
0<a b+1.
b+1.
故当0<b 1时,对任意x
1时,对任意x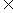 [0,1],都有|f(x)|
[0,1],都有|f(x)| 1的充要条件为0<a
1的充要条件为0<a b+1.
b+1.
点评:含参数的二次函数与绝对值不等式相综合,这是历年高考命题的热点之一.在备考复习时,应当重视这类题型的解题技巧,掌握一些解题的套路,领悟当中的变化技能,反复思考参数的处理艺术.
6.不等式 的解集是___________
的解集是___________
简答:1-4.CDAD; 5. {x|x≥-1}; 6. 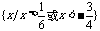
5.(2004年全国卷I)不等式|x+2|≥|x|的解集是 .
4. (2004全国IV)不等式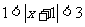 的解集为 ( )
的解集为 ( )
A.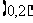 B.
B.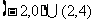 C.
C. D.
D.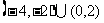
3.(2006北京)在下列四个函数中,满足性质:“对于区间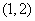 上的任意
上的任意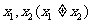 ,
,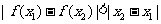 恒成立”的只有( )
恒成立”的只有( )
A.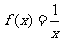 B.
B.
C.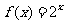 D.
D.
2.(2004福建)命题p:若a、b∈R,则|a|+|b|>1是|a+b|>1的充分而不必要条件;
命题q:函数y= 的定义域是(-∞,-1
的定义域是(-∞,-1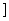 ∪[3,+∞
∪[3,+∞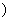 .则( )
.则( )
A.“p或q”为假 B.“p且q”为真
C.p真q假 D.p假q真
1.(2006江苏) 设a、b、c是互不相等的正数,则下列不等式中不恒成立的是( )
A.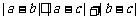 B.
B.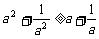
C.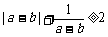 D.
D.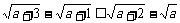
3. 解绝对值不等式的基本思想:去绝对值符号;具体方法有:
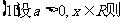
 ,
, 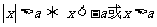
一般地: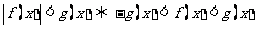

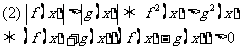
(3)分段去绝对值,找出零点,分段求解。
(4)数形结合.
2.绝对值的运算性质
 (注意不等式成立的条件)
(注意不等式成立的条件)
 (注意不等式成立的条件)
(注意不等式成立的条件)
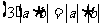 ;
;

1. 绝对值的定义和性质: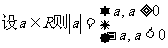
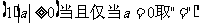 ;
; 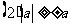
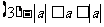

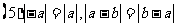
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com