
6.该日下列说法中不正确的是 ( )
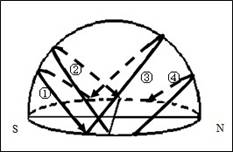 A.澳大利亚北部盛行西北风 B.尼罗河河水泛滥
A.澳大利亚北部盛行西北风 B.尼罗河河水泛滥
C.巴西高原草原一片枯黄 D.北极考察的好时机
5.乙地的正午太阳高度为 ( )
A.22º B.44º C.11º D.68º
4.甲地的地理纬度为 ( )
A.23º26’N B.66º34’N
C.22ºN D.90ºN
3、 ∠3=33°,那么∠4为
A.22° B 44° C 11° D 33°
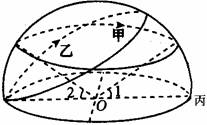 下图为北半球甲乙两地某日“太阳视运动路线图”,圆O为地平圈,箭头为太阳视运动方向,<1=<2=22º。回答4-6题。
下图为北半球甲乙两地某日“太阳视运动路线图”,圆O为地平圈,箭头为太阳视运动方向,<1=<2=22º。回答4-6题。
2、乙地的正午太阳高度
A.22° B.44° C. 11° D.68°
1、甲地的地理纬度
A.22°N B。23°26′N
C . 66°34′N D. 90°N
10. 设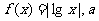 、b是满足
、b是满足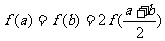 的实数,其中
的实数,其中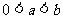 .
.
⑴求证: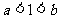 ;
⑵求证:
;
⑵求证: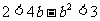 .
.
解:(1)由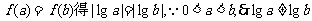 只能
只能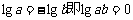
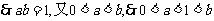
(2)由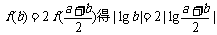
由于a、b为正数,
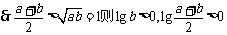 ,
,
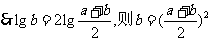
即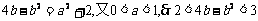
[探索题]已知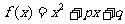 ,求证:
,求证:
(1) 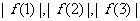 中至少有一个不小于
中至少有一个不小于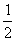 。
。
(2) 若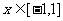 时,
时,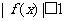 ,求证:|p|≤1.
,求证:|p|≤1.
[分析]由于题(1)的结论是:三个函数值中“至少有一个不小于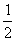 ”,情况较复杂,会出现多个异向不等式组成的不等式组,一一证明十分繁冗,而结论的反面构成三个同向不等式,结构简单,故采用反证法为宜。
”,情况较复杂,会出现多个异向不等式组成的不等式组,一一证明十分繁冗,而结论的反面构成三个同向不等式,结构简单,故采用反证法为宜。
证明(1)(反证法)假设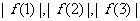 都小于
都小于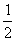 ,则
,则
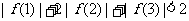 ,
,
而 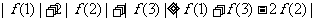
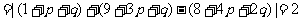 ,相互矛盾
,相互矛盾
∴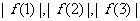 中至少有一个不小于
中至少有一个不小于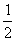 。
。
(2)由已知得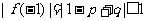 ,
,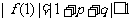
∴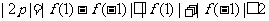 ∴
∴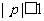
9.已知f(x)=x2-x+c定义在区间[0,1]上,x1、x2∈[0,1],且x1≠x2,求证:
(1)f(0)=f(1);
(2)| f(x2)-f(x1)|<|x1-x2|;
(3)|
f(x1)-f(x2)|<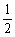 ;
;
(4)|
f(x1)-f(x2)|≤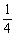 .
.
证明:(1)f(0)=c,f(1)=c,
∴f(0)=f(1).
(2)| f(x2)-f(x1)|=|x2-x1||x2+x1-1|.
∵0≤x1≤1,∴0≤x2≤1,0<x1+x2<2(x1≠x2).
∴-1<x1+x2-1<1.
∴| f(x2)-f(x1)|<|x2-x1|.
(3)不妨设x2>x1,由(2)知
| f(x2)-f(x1)|<x2-x1. ①
而由f(0)=f(1),从而
| f(x2)-f(x1)|=| f(x2)-f(1)+f(0)-f(x1)|
≤| f(x2)-f(1)|+| f(0)-f(x1)|<|1-x2|+|x1|<1-x2+x1. ②
①+②得2| f(x2)-f(x1)|<1,
即| f(x2)-f(x1)|<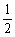 .
.
(4)|f(x2)-f(x1)|≤fmax-fmin=f(0)-f(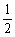 )=
)=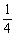 .
.
8.求证:(1)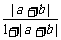 ≤
≤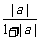 +
+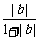 .
.
(2) 如果设m等于 ,
,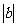 和1中最大的一个,
和1中最大的一个,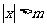 时,则
时,则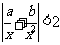 .
.
证明(1):令f(x)=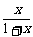 (x≥0),易证f(x)在[0,+∞)上单调递增.
(x≥0),易证f(x)在[0,+∞)上单调递增.
|a+b|≤|a|+|b|,
∴f(|a+b|)≤f(|a|+|b|),
即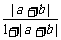 ≤
≤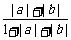 =
=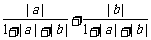 ≤
≤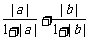 .
.
法2:分析法
当|a+b|=0时,不等式成立;
当|a+b|≠0时,原不等式即为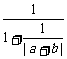 ≤
≤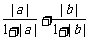 .
.
∵|a+b|≤|a|+|b|,
∴左边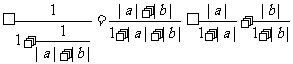
(2)(综合法)由已知得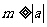 ,
,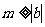 ,
,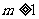 ,
,
从而知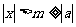 ,
, 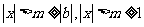

7.解不等式
(1) |x2─3|x|─3|£1; (2)|x-x2-2|>x2-3x-4 (x>-3)
解:(1) ∵|x2─3|x|─3|£1
∴─1£x2─3|x|─3£1
∴ Þ
Þ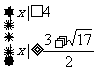
∴ 原不等式的解是: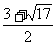 £x£4或─4£x£
£x£4或─4£x£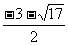
点评:本题由于运用了x∈R时,x2=|x|2从而避免了一场大规模的讨论
(2)法1:原不等式等价于:x-x2-2<-(x2-3x-4) ①
或:x-x2-2>x2-3x-4 ②
解①得:x>1, 解②得: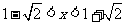
∴原不等式的解集为: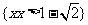 .
.
法2: ……
……
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com