
学科网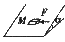 1.如图所示,物体M位于倾角为
1.如图所示,物体M位于倾角为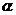 的斜面上,在平行于斜面的水平力F的作用下处于静止状态.如果将外力F撤去,则下列说法正确的是
的斜面上,在平行于斜面的水平力F的作用下处于静止状态.如果将外力F撤去,则下列说法正确的是
20.(本小题满分14分)
(1)由an+1=an+6an-1,an+1+2an=3(an+2an-1) (n≥2)
∵a1=5,a2=5 ∴a2+
故数列{an+1+2an}是以15为首项,3为公比的等比数列………………5分
(2)由(1)得an+1+2an=5?3n
由待定系数法可得(an+1-3n+1)=-2(an-3n)
即an-3n=2(-2)n-1
故an=3n+2(-2)n-1=3n-(-2)n…………………………………………10分
(3)由3nbn=n(3n-an)=n[3n-3n+(-2)n]=n(-2)n,∴bn=n(-)n
令Sn=|b1|+|b2|+…+|bn|=+2()2+3()3+…+n()n
Sn=()2+2()3+…+(n-1)()n+n()n+1
…………12分
得Sn=+()2+()3+…+()n-n()n+1
=-n()n+1=2[1-()n]-n()n+1
∴ Sn=6[1-()n]-3n()n+1<6
要使得|b1|+|b2|+…+|bn|<m对于n∈N*恒成立
只须m≥6………………………………………………………14分
21.(本小题满分14分) 已知数列{an}满足a1=5,a2=5,an+1=an+6an-1(n≥2).
(1)求证:{an+1+2an}是等比数列;
(2)求数列{an}的通项公式;
(3)设3nbn=n(3n-an),且|b1|+|b2|+…+|bn|<m对于n∈N*恒成立,
求m的取值范围.
综上 、
、 知
知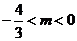

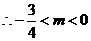 .
.
由(*)式恒成立,必有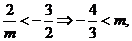 又
又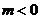 .
.
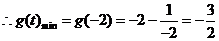 .
.
则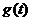 在区间
在区间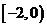 是单调增函数
是单调增函数
令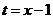 ,则
,则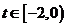 ,记
,记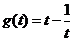 ,
,
(*)式化为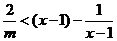 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com