22．(本小题满分14分)

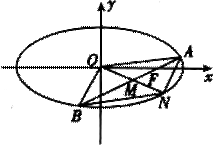
　　　 如图，已知椭圆C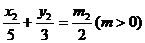：，经过椭圆C的右焦点F且斜率为k(k≠0)的直线l交椭圆G于A、B两点，M为线段AB的中点，设O为椭圆的中心，射线OM交椭圆于N点．

　　　 (1)是否存在k，使对任意m>0，总有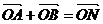成立？若存在，求出所有k的值；

　　　 (2)若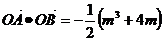，求实数k的取值范围．

21．(本小题满分12分)

　　　 设数列{a_n}的各项都是正数，且对任意n∈N*,都有a₁³+a₂³+a₃³+…+a_n³＝S_n²，其中Sn为数例{a_n}的前n项和．

　　　 (1)求证：a_n²＝2S_n－a_n；

　　　 (2)求数列{a_n}的通项公式；

　　　 (3)设b_n＝3ⁿ+(－1)^n－1λ·2a_n(λ为非零整数，n∈N*)，试确定λ的值，使得对任意n∈N*,都有b_n+1>b_n成立．

20．(本小题满分12分)

　　　 函数y＝f(x)是定义域为R的奇函数，且对任意的x∈R,均有f(x+4)＝f(x)成立，当x∈(0,2)时，f(x)＝－x²+2x+1．

　　　 (1)当x∈[4k－2,4k+2](k∈Z)时，求函数f(x)的表达式；

　　　 (2)求不等式f(x)>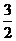的解集．

19．(本小题满分12分)

　　　 甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内任何时刻到达是等可能的．

　　　 (1)如果甲船和乙船的停泊时间都是4小时，求它们中的任何一条船 不需要等等码头空出的概率；

　　　 (2)如果甲船的停泊时间为4小时，乙船的停泊时间是2小时，求它们中的任何一条船 不需要等待码头空出的概率．

18．(本小题满分12分)

如图，在五面体，ABCDF中，点O是矩形ABCD的对角线的交点，面ABF是等边三角形，棱EF＝．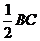

　　　 (1)证明EO∥平面ABF；

　　　 (2)问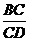为何值是，有OF⊥ABE，试证明你的结论．

17．(本小题满分12分)

在△ABC中，角A、B、C所对的边分别是a、b、c，则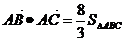(其中S_△ABC为△ABC的面积)．

(1)求sin²；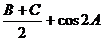

(2)若b＝2,△ABC的面积S△ABC＝3，求a．

16．设函数f(x)＝sin(ω+φ)(ω>0,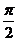－),有下列论断：

①f(x)的图象关于直线x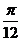＝对称；　　　　　 ②f(x)的图象关于(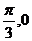)对称；

③f(x)的最小正周期为π；　　　　　　　　　　　　　 ④在区间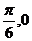［－］上，f(x)为增函数．

以其中的两个论断为条件，剩下的两个论断为结论，写出你认为正确的一个命题：若___________，则_________________．(填序号即可)

15．某商场在节假日对顾客购物实行一定的优惠，商场规定：

①如一次购物不超过200元，不给予折扣；

②如一次购物超过200元不超过500元，按标价给予九折优惠；

③如一次购物超过500元的，其中500元给予九折优惠，超过500元的剩余部分给予八五折优惠．

某人两次去购物，分别付款176元和432元，如果他只云一次购买同样的商品，则他应该付款为__________________元．

14．一个总体依有100个个体，随机编号0，1，2，…，99，依从小到大的编号顺序平均分成10个小组，组号依次为1，2，3，…，10，现用系统抽样方法抽取一个容量为10的样本，规定如果在第1组随机抽取的号码为m，那么在第k组中抽取的号码个位数字与m+k的个位数字相同，若m＝8，则在第8组中抽取的号码是_________．

13．已知一圆锥的侧面展开图为半圆，且面积为S，则圆锥的底面面积是__________．