
2.已知物体的运动方程为 (t是时间,s是位移),则物体在时刻t=2时的速度为
(t是时间,s是位移),则物体在时刻t=2时的速度为
A. 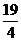 B.
B.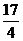 C.
C. D.
D. 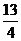
1.函数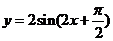 是
是
A.周期为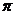 的奇函数 B.周期为
的奇函数 B.周期为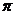 的偶函数
的偶函数
C.周期为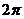 的奇函数 D.周期为
的奇函数 D.周期为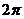 的偶函数
的偶函数
20. (本题满分14分)已知函数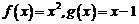 .
.
(1)若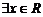 使
使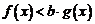 ,求实数
,求实数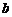 的取值范围;
的取值范围;
(2)设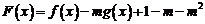 ,且
,且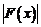 在
在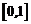 上单调递增,求实数
上单调递增,求实数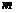 的取值范围.
的取值范围.
中山市高三级2008-2009学年度第一学期期末统一考试
19. (本题满分14分)已知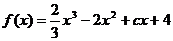 ,
,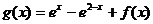 ,
,
 (1)若f(x)在
(1)若f(x)在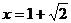 处取得极值,试求c的值和f(x)的单调增区间;
处取得极值,试求c的值和f(x)的单调增区间;
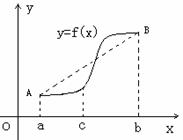
(2)如右图所示,若函数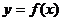 的图象在
的图象在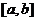 连续光滑,试猜想拉格朗日中值定理:即一定存在
连续光滑,试猜想拉格朗日中值定理:即一定存在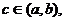 使得
使得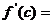 ?(用含有a,b,f(a),f(b)的表达式直接回答)
?(用含有a,b,f(a),f(b)的表达式直接回答)
(3)利用(2)证明:函数y=g(x)图象上任意两点的连线斜率不小于2e-4.
18. (本题满分14分)如图,四面体ABCD中,O、E分别是BD、BC的中点,
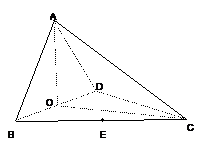
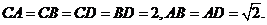
(I)求证: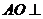 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦;
(III)求点E到平面ACD的距离.
17.(本小题满分14分)已知10件产品中有3件是次品.
(I)任意取出3件产品作检验,求其中至少有1件是次品的概率;
(II)为了保证使3件次品全部检验出的概率超过0.6,最少应抽取几件产品作检验?
16. (本题满分12分)已知数列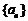 是首项为
是首项为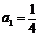 ,公比
,公比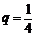 的等比数列,设
的等比数列,设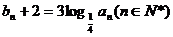 ,数列
,数列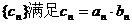 .
.
(1)求数列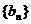 的通项公式;(2)求数列
的通项公式;(2)求数列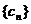 的前n项和Sn.
的前n项和Sn.
15. (本题满分12分)
已知向量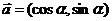 ,
, 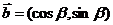 ,
, 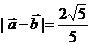 .
.
(Ⅰ)求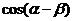 的值;
的值;
(Ⅱ)若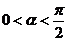 ,
, 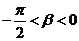 , 且
, 且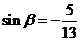 , 求
, 求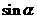 .
.
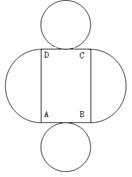
14.为迎接校庆,学校准备投入a元建造一个花圃(如图).已知矩形ABCD的造价为40元/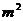 ,其余的两个半圆及两个圆的造价为20元/
,其余的两个半圆及两个圆的造价为20元/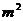 .两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,
.两圆的直径分别为矩形的长和宽,由于矩形ABCD要种名贵花卉,故建造时要求矩形ABCD的面积越大越好.那么,当矩形ABCD的面积达到最大时,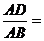
13.以下有四种说法:
(1)若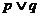 为真,
为真,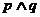 为假,则
为假,则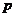 与
与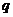 必为一真一假;
必为一真一假;
(2)若数列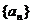 的前
的前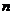 项和为
项和为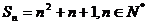 ,则
,则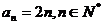 ;
;
(3)若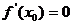 ,则
,则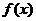 在
在 处取得极值;
处取得极值;
 (4)由变量x和y的数据得到其回归直线方程
(4)由变量x和y的数据得到其回归直线方程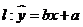 ,则
,则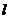 一定经过点
一定经过点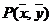 .
.
以上四种说法,其中正确说法的序号为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com