
2.已知物体的运动方程为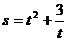 (t是时间,s是位移),则物体在时刻t=2时的速度为
(t是时间,s是位移),则物体在时刻t=2时的速度为
A.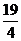 B.
B.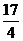 C.
C.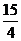 D.
D.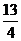
1.函数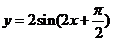 是
是
A.周期为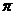 的奇函数 B.周期为
的奇函数 B.周期为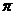 的偶函数
的偶函数
C.周期为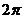 的奇函数 D.周期为
的奇函数 D.周期为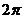 的偶函数
的偶函数
22.(本题满分14分)
在直角坐标系中,已知一个圆心在坐标原点,半径为2的圆,从这个圆上任意一点P向y轴作垂线段PP′,P′为垂足.
(1)求线段PP′中点M的轨迹C的方程;
(2)过点Q(-2,0)作直线l与曲线C交于A、B两点,设N是过点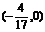 ,且以
,且以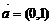 为方向向量的直线上一动点,满足
为方向向量的直线上一动点,满足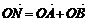 (O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
(O为坐标原点),问是否存在这样的直线l,使得四边形OANB为矩形?若存在,求出直线l的方程;若不存在,说明理由.
21.(本小题满分12分)已知函数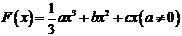 且
且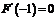
(1)若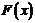 在
在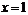 取得极小值-2,求函数
取得极小值-2,求函数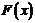 的单调区间
的单调区间
(2)令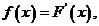 若
若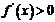 的解集为A,且
的解集为A,且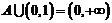 ,求
,求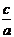 的范围
的范围
20.(本小题满分12分)造船厂年造船量20艘,造船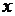 艘产值函数为
艘产值函数为
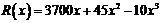 (单位:万元),成本函数
(单位:万元),成本函数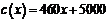 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数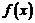 的边际函数
的边际函数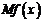 定义为
定义为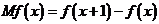
(1)求利润函数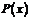 及边际利润函数
及边际利润函数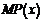 (利润=产值-成本)
(利润=产值-成本)
(2)问年造船量安排多少艘时,公司造船利润最大
(3)边际利润函数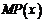 的单调递减区间
的单调递减区间
19.(理做Ⅰ、Ⅱ、Ⅲ;文做Ⅰ、Ⅳ)
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F
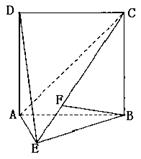 为CE上的点,且BF⊥平面ACE.
为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证:AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的余弦值;
(Ⅲ)求点D到平面ACE的距离.
(Ⅳ)求证:平面BDF⊥平面ABCD
18.已知等比数列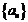 中,
中,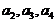 分别是某等差数列的第5项,第3项,第2项,且
分别是某等差数列的第5项,第3项,第2项,且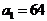 ,公比
,公比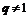 ;
;
(1)求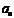
(2)设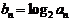 ,求数列
,求数列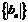 的前n项和
的前n项和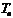 。
。
17.已知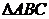 中,角A,B,C,所对的边分别是
中,角A,B,C,所对的边分别是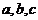 ,且
,且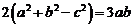 ;
;
(1)求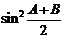
(2)若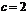 ,求
,求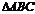 面积的最大值。
面积的最大值。
16.设函数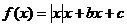 ,给出下列4个命题:
,给出下列4个命题:
①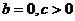 时,
时,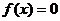 只有一个实数根; ②
只有一个实数根; ②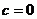 时,
时,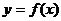 是奇函数;
是奇函数;
③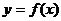 的图象关于点
的图象关于点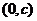 对称; ④方程
对称; ④方程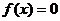 至多有2个实数根
至多有2个实数根
上述命题中的所有正确命题的序号是 .
15.已知F1、F2是椭圆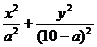 =1(5<a<10=的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
=1(5<a<10=的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com