
1.设全集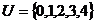 ,
,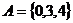 ,
,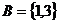 ,则
,则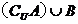 =( ▲ )
=( ▲ )
A.{2} B.{1,2,3} C.{1,3} D.{0,1,2,3,4}
22.(本小题满分15分)
(Ⅰ) 由题意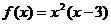 ,
,
由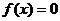 ,解得
,解得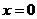 或
或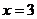 ;
--- 4分
;
--- 4分
(Ⅱ) 设此最小值为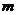 ,而
,而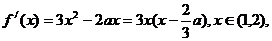
(1)当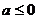 时,
时,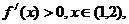
则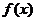 是区间[1,2]上的增函数, 所以
是区间[1,2]上的增函数, 所以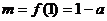 ;
--- 3分
;
--- 3分
(2)当 时,
时,
在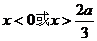 时,
时,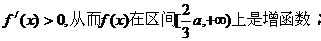
在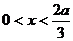 时,
时,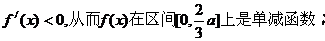 --- 3分
--- 3分
① 当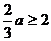 ,即
,即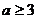 时,
时, ;
;
② 当 ,即
,即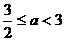 时,
时,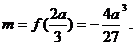
③ 当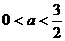 时,
时,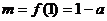 .
.
综上所述,所求函数的最小值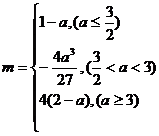 .
--- 5分
.
--- 5分
21.(本小题满分15分)
(I)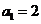 ,
,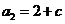 ,
,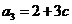 ,因为
,因为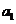 ,
,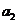 ,
,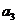 成等比数列,
成等比数列,
所以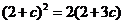 ,解得
,解得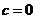 (舍)或
(舍)或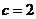 .
.
故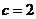 ;
--- 5分
;
--- 5分
(II)当 时,由于
时,由于
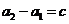 ,
,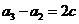 ,
,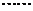
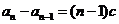 ,
,
所以 .
.
又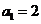 ,
,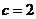 ,故
,故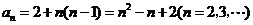 .
.
当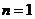 时,上式也成立,所以
时,上式也成立,所以 ;
--- 5分
;
--- 5分
(Ⅲ)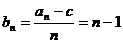 ;
;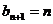 .
.
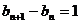 ,∴数列
,∴数列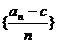 是等差数列.
--- 5分
是等差数列.
--- 5分
20. (本小题满分14分)
(Ⅰ) ∵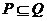 , 当
, 当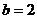 时,
时,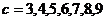 ;
;
当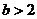 时,
时,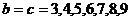 .基本事件总数为14.
--- 4分
.基本事件总数为14.
--- 4分
其中,b = c的事件数为7种.
所以b=c的概率为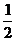 .
---- 3分
.
---- 3分
(Ⅱ) 记“方程有实根”为事件A,
若使方程有实根,则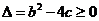 ,即
,即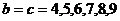 ,共6种. --- 4分
,共6种. --- 4分
∴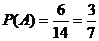 .
--- 3分
.
--- 3分
19. (本小题满分14分)
(Ⅰ) 当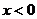 时,
时,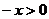 ,
,
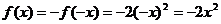 ;
--- 6分
;
--- 6分
(Ⅱ)若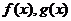 在
在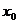 处的切线互相平行,则
处的切线互相平行,则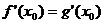 ,
--- 4分
,
--- 4分
 ,解得,
,解得, 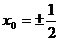
∵x > 0 , 得.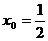 --- 4分
--- 4分
18. (本小题满分14分)
(Ⅰ) 
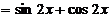 ,
--- 3分
,
--- 3分
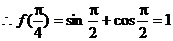 --- 3分
--- 3分
(Ⅱ) 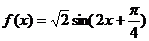 ,
---
3分
,
---
3分
当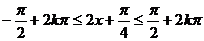 (
(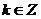 )时,f(x)单增,
--- 2分
)时,f(x)单增,
--- 2分
即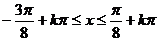 (
(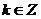 ) ∵
) ∵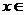
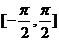 ,
,
∴ 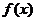 在
在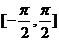 上的单调递增区间为
上的单调递增区间为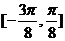 .
--- 3分
.
--- 3分
15.  16.
8
17. ②
16.
8
17. ②
11.16
12. 3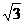 13. 1200 14.
13. 1200 14.

(18)(本题14分)已知向量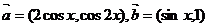
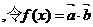 .
.
(Ⅰ) 求 f (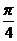 )的值;
)的值;
(Ⅱ)求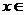
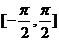 时,f (x)的单调递增区间.
时,f (x)的单调递增区间.
(19)(本题14分)设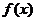 是定义在
是定义在 上的奇函数,且当
上的奇函数,且当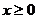 时,
时,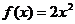 .
.
(Ⅰ) 求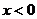 时,
时,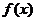 的表达式;
的表达式;
(Ⅱ) 令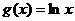 ,问是否存在
,问是否存在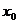 ,使得
,使得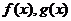 在x = x0处的切线互相平行?若存在,请求出
在x = x0处的切线互相平行?若存在,请求出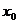 值;若不存在,请说明理由.
值;若不存在,请说明理由.
(20)(本题14分)设集合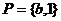 ,
,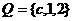 ,
,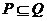 , 若
, 若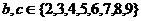 .
.
(Ⅰ) 求b = c的概率;
(Ⅱ)求方程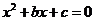 有实根的概率.
有实根的概率.
(21) (本题15分)数列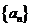 中,
中,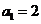 ,
,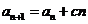 (
(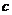 是不为零的常数,
是不为零的常数,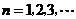 ),且
),且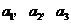 成等比数列.
成等比数列.
(Ⅰ) 求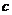 的值;
的值;
(Ⅱ)求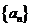 的通项公式;
的通项公式;
(Ⅲ)证明数列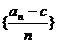 是等差数列.
是等差数列.
(22)
(本题15分)已知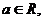 函数
函数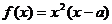 .
.
(Ⅰ)当a=3时,求f(x)的零点;
(Ⅱ)求函数y=f (x)在区间 [ 1,2 ] 上的最小值.
2009年杭州市第一次高考科目教学质量检测
数学参考评分标准(文科)
(11) 若数列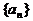 满足条件:
满足条件: 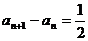 ,且
,且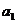 =
=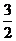 , 则
, 则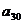 = _ __.
= _ __.
(12)在△ABC中,若∠B=60°,sinA=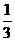 ,BC=2,则 AC= ___ .
,BC=2,则 AC= ___ .
(13)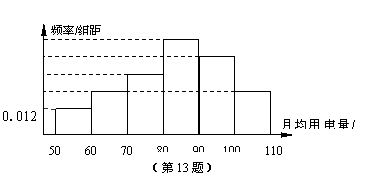 某地为了了解该地区10000户家庭用电情况,采用分层抽样的方法抽取了500户家庭的月均用电量,并根据这500户家庭月均用电量画出频率分布直方图(如图),则该地区10000户家庭中月均用电度数在[70,80]的家庭有________户.
某地为了了解该地区10000户家庭用电情况,采用分层抽样的方法抽取了500户家庭的月均用电量,并根据这500户家庭月均用电量画出频率分布直方图(如图),则该地区10000户家庭中月均用电度数在[70,80]的家庭有________户.
(14) 设函数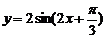 的图象关于点P
的图象关于点P 成中心对称,若
成中心对称,若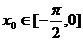 ,则
,则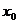 =_____.
=_____.
(15) 从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
(16) 若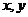 满足条件
满足条件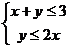 ,则
,则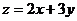 的最大值是 ____ .
的最大值是 ____ .
(17) 在下列五个函数中:①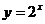 ; ②
; ②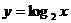 ; ③
; ③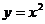 ; ④
; ④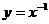 ; ⑤
; ⑤ ,
,
当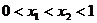 时,使
时,使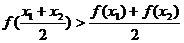 恒成立的函数是______(将正确的序
恒成立的函数是______(将正确的序
号都填上).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com