
2、散点图的作用是判断两个变量更近似于什么样的函数关系。
1、 回归直线方程通过样本点的中心:
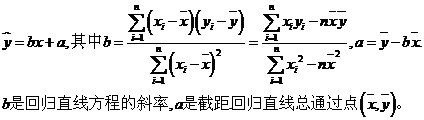
线性相关系数:
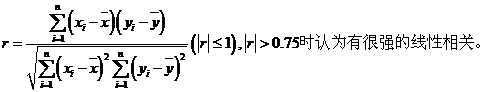
6、正态分布:(1)定义:如果随机变量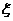 的总体密度曲线是由或近似地由下面的函数给定:
的总体密度曲线是由或近似地由下面的函数给定:
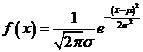 ,x∈R,则称
,x∈R,则称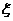 服从正态分布,这时的总体分布叫正态分布,其中
服从正态分布,这时的总体分布叫正态分布,其中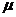 表示总体平均数,
表示总体平均数,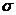 叫标准差,正态分布常用
叫标准差,正态分布常用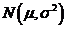 来表示,当
来表示,当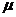 =0,
=0,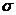 =1时,称
=1时,称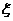 服从标准正态分布,这时的总体叫标准正态总体。
服从标准正态分布,这时的总体叫标准正态总体。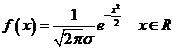 叫标准正态曲线。
叫标准正态曲线。
(2)、正态曲线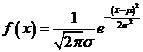 ,x∈R的有关性质:1)曲线在x轴上方,与x轴永不相交,曲线与x轴之间的部分的面积为1,2)曲线关于直线x=
,x∈R的有关性质:1)曲线在x轴上方,与x轴永不相交,曲线与x轴之间的部分的面积为1,2)曲线关于直线x=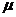 对称,且在x=
对称,且在x=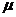 两旁延伸时无限接近x轴,3)曲线在x=
两旁延伸时无限接近x轴,3)曲线在x=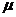 处达到最高点,峰值为
处达到最高点,峰值为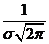 ,(4)当
,(4)当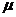 一定时,曲线形状由
一定时,曲线形状由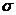 的大小来决定,
的大小来决定,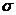 越大,曲线越“矮胖”,表示总体分布比较离散,
越大,曲线越“矮胖”,表示总体分布比较离散,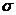 越小,曲线越“瘦高”,表示总体分布比较集中。
越小,曲线越“瘦高”,表示总体分布比较集中。
(3)、在标准正态总体N(0,1)中:(1)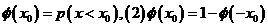 (因为曲线关于y轴对称)
(因为曲线关于y轴对称)
(4)、
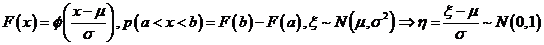
(5)、
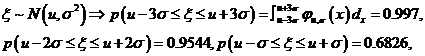
第二十五讲统计案例
5、条件概率定义
:设A和B为两个事件,P(A)>0,那么,在“A已发生”的条件下,B发生的条件概率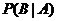 读作A 发生的条件下 B 发生的概率.
读作A 发生的条件下 B 发生的概率.
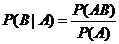 .
.
由这个定义可知,对任意两个事件A、B,若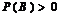 ,则有
,则有
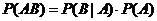 .
.
如果B,C是两个互斥事件,则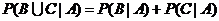 .
.
练习:一个正方形被平均分成9个部分,向大正方形区域随机地投掷一个点(每次都能投中),设投中最左侧3个小正方形区域的事件记为A,投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B,求P(AB),P(A︱B)。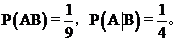
4、称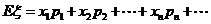 为
为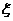 的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
称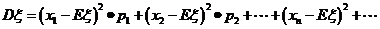 为
为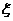 的均方差,简称为方差,
的均方差,简称为方差,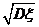 叫做随机变量
叫做随机变量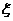 的标准差,记作:
的标准差,记作: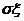 。
。
易证:(1)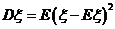 ,
,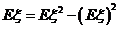 。
。
(2)若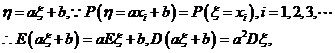
(3)若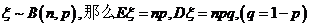
(4)若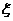 服从几何分布,则
服从几何分布,则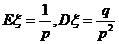
如(1)有一组数据:x1,x2,…,xn(x1≤x2≤…≤xn),它们的算术平均值为20,若去掉其中的xn,余下数据的算术平均值为18,则xn关于n的表达式为 。
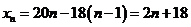
(2)已知数据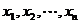 的平均数
的平均数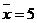 ,方差
,方差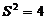 ,则数据
,则数据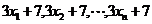 的平均数和标准差分别为
( D ) A.15,36 B.22,6 C.15,6 D.22,36
的平均数和标准差分别为
( D ) A.15,36 B.22,6 C.15,6 D.22,36
3、在独立重复的试验中,某事件第一次发生时所作试验的次数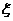 也是一个取值为正整数的离散型随机变量,“
也是一个取值为正整数的离散型随机变量,“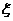 =k”表示在第k次独立重复的试验时事件第一次发生。如果把第k次试验时事件A发生记为
=k”表示在第k次独立重复的试验时事件第一次发生。如果把第k次试验时事件A发生记为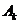 ,事件A不发生记为
,事件A不发生记为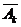 ,
,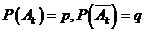 ,那么
,那么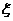 服从几何分布。
服从几何分布。
记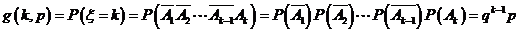
其中q=1-p,k=1,2,3,…
2、如果在1次试验中某事件发生的概率是p,那么在n次独立重复的试验中这个事件发生k次的概率是: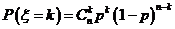 ,k=0,1,2,…n.这时因为
,k=0,1,2,…n.这时因为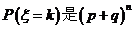 展开式中的第k+1项,称
展开式中的第k+1项,称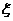 服从二项分布,记作
服从二项分布,记作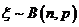 ,并记
,并记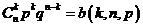
n=1时,称为贝努利分布。
1、如果随机变量可能取的值是可数的,或者说可以按一定次序一一列出的,那么,这样的随机变量叫做离散型随机变量。如果随机变量可以取某一区间内的一切值,那么这样的随机就是叫做连续型随机变量。
如果离散型随机变量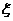 可能取的值为x
可能取的值为x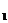 ,x
,x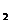 ,x
,x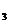 …x
…x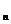 ,…,而
,…,而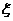 取每一个值x
取每一个值x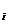 (i=1,2,3,…)的概率P(
(i=1,2,3,…)的概率P(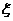 =x
=x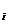 )=p
)=p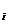 ,那么如下表所示
,那么如下表所示
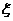 |
x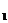 |
x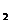 |
x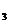 |
… |
x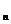 |
… |
|
p |
p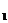 |
p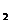 |
p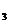 |
… |
p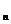 |
… |
就称为随机变量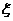 的分布列。具有下列性质:(1)0≤p
的分布列。具有下列性质:(1)0≤p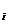 ≤1,(i=1,2,3,…),(2)p
≤1,(i=1,2,3,…),(2)p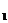 +p
+p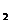 + p
+ p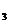 +…p
+…p +…=1(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
+…=1(3)离散型随机变量在某一范围内取值的概率等于它取这个范围内各个值的概率之和。
7、二项式定理的应用:二项式定理的主要应用有近似计算、证明整除性问题或求余数、应用其首尾几项进行放缩证明不等式。
如(1)(0.998)5精确到0.001近似值为____0.990 ____;
(2)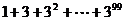 被4除所得的余数为__
___;
被4除所得的余数为__
___;
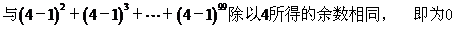
(3)今天是星期一,10045天后是星期___ 二 __;
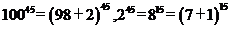
(4)求证: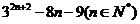 能被64整除;
能被64整除;
(5)求证: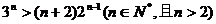
第二十四讲随机就是及其分布
7、二项式定理的应用:二项式定理的主要应用有近似计算、证明整除性问题或求余数、应用其首尾几项进行放缩证明不等式。
如(1)(0.998)5精确到0.001近似值为____0.990 ____;
(2)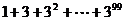 被4除所得的余数为__
___;
被4除所得的余数为__
___;
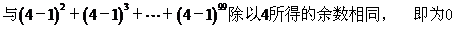
(3)今天是星期一,10045天后是星期___ 二 __;
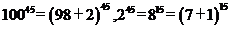
(4)求证: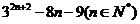 能被64整除;
能被64整除;
(5)求证: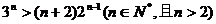 6、(1)二项式定理:(a+b)
6、(1)二项式定理:(a+b)  =C
=C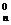 a
a + C
+ C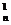 a
a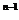 b+…+ C
b+…+ C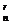 a
a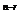 b
b +…+C
+…+C b
b n∈N,它共有n+1项,其中C
n∈N,它共有n+1项,其中C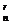 (r=0,1,2…n)叫做二项式系数,C
(r=0,1,2…n)叫做二项式系数,C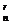 a
a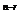 b
b 叫做二项式的通项,用T
叫做二项式的通项,用T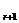 表示,即通项为展开式的第r+1项,T
表示,即通项为展开式的第r+1项,T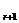 =C
=C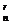 a
a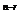 b
b ,
,
特别提醒:(1)项的系数与二项式系数是不同的两个概念,但当二项式的两个项的系数都为1时,系数就是二项式系数。如在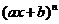 的展开式中,第r+1项的二项式系数为
的展开式中,第r+1项的二项式系数为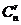 ,第r+1项的系数为
,第r+1项的系数为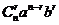 ;而
;而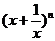 的展开式中的系数就是二项式系数;
的展开式中的系数就是二项式系数;
(2)当n的数值不大时往往借助杨辉三角直接写出各项的二项式系数;
(3)审题时要注意区分所求的是项还是第几项?求的是系数还是二项式系数?
如:(1)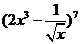 的展开式中常数项是_
___;
的展开式中常数项是_
___;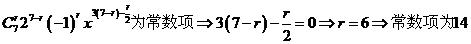
(2)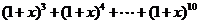 的展开式中的
的展开式中的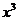 的系数为______ ;
的系数为______ ;
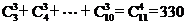
(3)数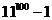 的末尾连续出现零的个数是_ 3个
___;
的末尾连续出现零的个数是_ 3个
___;
(4)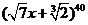 展开后所得的
展开后所得的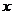 的多项式中,系数为有理数的项共有_ 7 ___项;
的多项式中,系数为有理数的项共有_ 7 ___项;
(5)若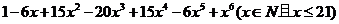 的值能被5整除,则
的值能被5整除,则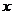 的可
的可
取值的个数有__ 5
__个;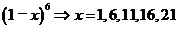
(6)若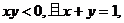 二项式
二项式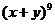 按
按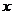 降幂展开后,其第二项不大于第三项,则
降幂展开后,其第二项不大于第三项,则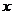 的取值范围是 ;
的取值范围是 ;
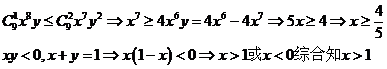
(7)函数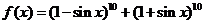 的最大值是_______
.
的最大值是_______
.
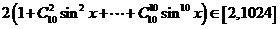
(2)、在二项式定理中,对a,b取不同的值可推出许多常用的式子:
(1)(1+x) =1+C
=1+C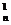 x+C
x+C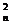 x
x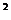 +…+C
+…+C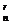 x
x +…+x
+…+x (a=1,b=x)
(a=1,b=x)
(2) C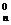 + C
+ C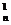 +…+ C
+…+ C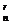 +…+C
+…+C =2
=2 (a=b=1)
(a=b=1)
(3) C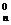 + C
+ C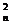 +
+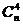 +…= C
+…= C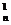 +
+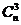 +…=2
+…=2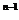 (a=1 b=-1)
(a=1 b=-1)
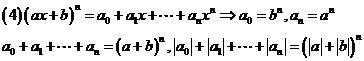
应用“赋值法”可求得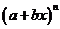 二项展开式中各项系数和为
二项展开式中各项系数和为 、“奇数 (偶次)项”系数和为
、“奇数 (偶次)项”系数和为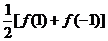 ,以及“偶数 (奇次)项”系数和为
,以及“偶数 (奇次)项”系数和为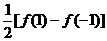 。
。
如(1)如果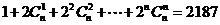 ,则
,则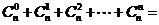 ;
;
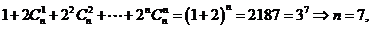
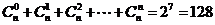
(2)化简 得
得
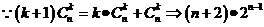
(3)已知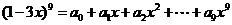 ,则
,则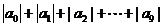 等于__ ;
等于__ ;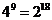
(4)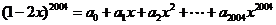 ,则
,则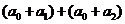 +
+
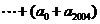 =_
____;
=_
____;
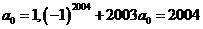
(5)设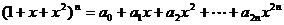 ,则
,则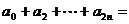 _____。
_____。
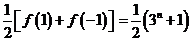
(3)、杨辉三角: 1
3
1 (a+b)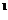
1 2 1
(a+b)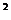
1 3 3 1
(a+b)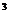
1 4 6 4 1
(a+b)
1 5 10 10 5 1 (a+b)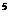
1 6 15 20 15 6 1 (a+b)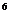
表中除1以外的其余各数都等于它肩上的两个数之和。
当n的数值不大时往往借助杨辉三角直接写出各项的二项式系数。
(4)、二项式系数的性质:
1)对称性:与首末两端“等距离”的两个二项式系数相等,即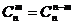
2)增减性与最大值:当r≤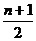 时,二项式系数C
时,二项式系数C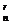 的值逐渐增大,当r≥
的值逐渐增大,当r≥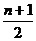 时,C
时,C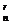 的值逐渐减小,且在中间取得最大值。当n为偶数时,中间一项的二项式系数
的值逐渐减小,且在中间取得最大值。当n为偶数时,中间一项的二项式系数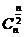 取得最大值。
取得最大值。
当n为奇数时,中间两项的二项式系数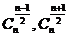 相等并同时取最大值
相等并同时取最大值
如(1)在二项式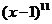 的展开式中,系数最小的项的系数为_____
的展开式中,系数最小的项的系数为_____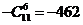 _
;
_
;
(2)在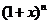 的展开式中,第十项是二项式系数最大的项,则
的展开式中,第十项是二项式系数最大的项,则 =___ 18
_。
=___ 18
_。
(5)、求二项式展开式中的系数绝对值最大的项常先判断系数的绝对值的单调性。求二项式展开式中的系数最大的项在上面的基础上再分析符号。
设第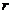 项的系数
项的系数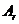 最大,由不等式组
最大,由不等式组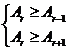 确定
确定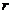 。或由
。或由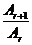 来确定。
来确定。
如求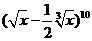 的展开式中,系数的绝对值最大的项和系数最大的项。
的展开式中,系数的绝对值最大的项和系数最大的项。

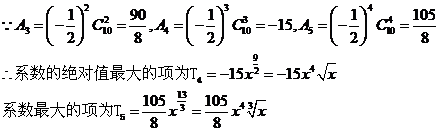
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com