
36.(2008 广东)将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边
AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD.
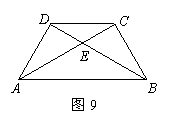
(1)填空:如图9,AC= ,BD= ;四边形ABCD是 梯形.
(2)请写出图9中所有的相似三角形(不含全等三角形).
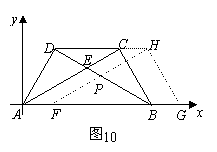
(3)如图10,若以AB所在直线为 轴,过点A垂直于AB的直线为
轴,过点A垂直于AB的直线为 轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向
轴建立如图10的平面直角坐标系,保持ΔABD不动,将ΔABC向 轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值值范围.
35.(2008 山东 聊城)如图,把一张长10cm,宽8cm的矩形硬纸板的四周各剪去一个同样大小的正方形,再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).

(1)要使长方体盒子的底面积为48cm2,那么剪去的正方形的边长为多少?
(2)你感到折合而成的长方体盒子的侧面积会不会有更大的情况?如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由;
(3)如果把矩形硬纸板的四周分别剪去2个同样大小的正方形和2个同样形状、同样大小的矩形,然后折合成一个有盖的长方体盒子,是否有侧面积最大的情况;如果有,请你求出最大值和此时剪去的正方形的边长;如果没有,请你说明理由.
34. (2008 河南实验区)如图,抛物线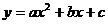 与
与 轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当
轴交于A、B两点(点A在点B左侧),与y轴交于点C,且当 =O和
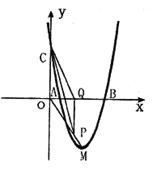
=O和 =4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
=4时,y的值相等。直线y=4x-16与这条抛物线相交于两点,其中一点的横坐标是3,另一点是这条抛物线的顶点M。
(1)求这条抛物线的解析式;
(2)P为线段OM上一点,过点P作PQ⊥ 轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
轴于点Q。若点P在线段OM上运动(点P不与点O重合,但可以与点M重合),设OQ的长为t,四边形PQCO的面积为S,求S与t之间的函数关系式及自变量t的取值范围;
(3)随着点P的运动,四边形PQCO的面积S有最大值吗?如果S有最大值,请求出S的最大值并指出点Q的具体位置和四边形PQCO的特殊形状;如果S没有最大值,请简要说明理由;
(4)随着点P的运动,是否存在t的某个值,能满足PO=OC?如果存在,请求出t的值。
33.(2008佳木斯市)如图,在平面直角坐标系中,点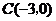 ,点
,点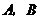 分别在
分别在 轴,
轴, 轴的正半轴上,且满足
轴的正半轴上,且满足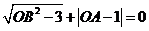 .
.
(1)求点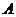 ,点
,点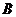 的坐标.
的坐标.
(2)若点 从
从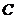 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线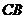 运动,连结
运动,连结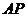 .设
.设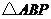 的面积为
的面积为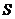 ,点
,点 的运动时间为
的运动时间为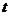 秒,求
秒,求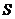 与
与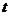 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,是否存在点 ,使以点
,使以点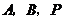 为顶点的三角形与
为顶点的三角形与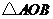 相似?若存在,请直接写出点
相似?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
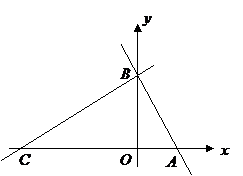

32.(2008佛山)我们所学的几何知识可以理解为对“构图”的研究:根据给定的(或构造的)几何图形提出相关的概念和问题(或者根据问题构造图形),并加以研究.
例如:在平面上根据两条直线的各种构图,可以提出“两条直线平行”、“两条直线相交”的概念;若增加第三条直线,则可以提出并研究“两条直线平行的判定和性质”等问题(包括研究的思想和方法).
请你用上面的思想和方法对下面关于圆的问题进行研究:
(1)
如图1,在圆O所在平面上,放置一条直线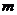 (
(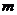 和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?
和圆O分别交于点A、B),根据这个图形可以提出的概念或问题有哪些(直接写出两个即可)?
(2)
如图2,在圆O所在平面上,请你放置与圆O都相交且不同时经过圆心的两条直线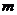 和
和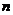 (
(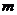 与圆O分别交于点A、B,
与圆O分别交于点A、B,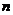 与圆O分别交于点C、D).
与圆O分别交于点C、D).
请你根据所构造的图形提出一个结论,并证明之.
(3) 如图3,其中AB是圆O的直径,AC是弦,D是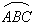
 的中点,弦DE⊥AB于点F. 请找出点C和点E重合的条件,并说明理由.
的中点,弦DE⊥AB于点F. 请找出点C和点E重合的条件,并说明理由.
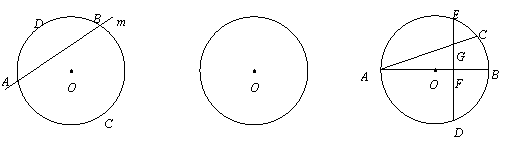
31.( 2008泰安)在等边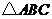 中,点
中,点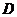 为
为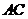 上一点,连结
上一点,连结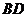 ,直线
,直线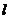 与
与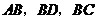 分别相交于点
分别相交于点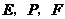 ,且
,且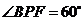 .
.
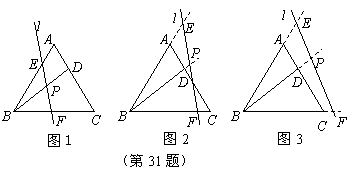

(1)如图1,写出图中所有与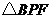 相似的三角形,并选择其中一对给予证明;
相似的三角形,并选择其中一对给予证明;
(2)若直线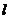 向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;
(3)探究:如图1,当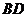 满足什么条件时(其它条件不变),
满足什么条件时(其它条件不变),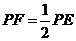 ?请写出探究结果,并说明理由.
?请写出探究结果,并说明理由.
(说明:结论中不得含有未标识的字母)
30. (2008年杭州市)在直角坐标系xOy中,设点A(0,t),点Q(t,b),平移二次函数
(2008年杭州市)在直角坐标系xOy中,设点A(0,t),点Q(t,b),平移二次函数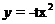 的图像,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交与B,C两点(∣OB∣<∣OC∣).连接AB.
的图像,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交与B,C两点(∣OB∣<∣OC∣).连接AB.
(1) 是否存在这样的抛物线F,使得∣OA∣2=∣OB∣·∣OC∣?请你说明理由;
(2)
如果AQ∥BC,且tan∠ABO=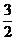 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。
29.(08厦门市)如图,在直角梯形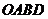 中,
中,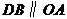 ,
,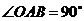 ,点
,点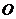 为坐标原点,点
为坐标原点,点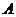 在
在 轴的正半轴上,对角线
轴的正半轴上,对角线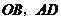 相交于点
相交于点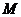 .
.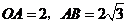 ,
,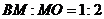 .
.
(1)求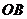 和
和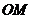 的值;
的值;
(2)求直线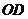 所对应的函数关系式;
所对应的函数关系式;
(3)已知点 在线段
在线段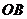 上(
上( 不与点
不与点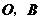 重合),经过点
重合),经过点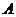 和点
和点 的直线交梯形
的直线交梯形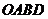 的边于点
的边于点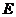 (
(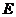 异于点
异于点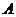 ),设
),设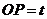 ,梯形
,梯形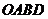 被夹在
被夹在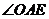 内的部分的面积为
内的部分的面积为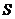 ,求
,求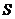 关于
关于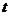 的函数关系式.
的函数关系式.
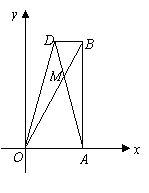

27.(08乌兰察布市)
两个直角边为6的全等的等腰直角三角形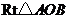 和
和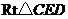 ,按如图一所示的位置放置,点
,按如图一所示的位置放置,点 与
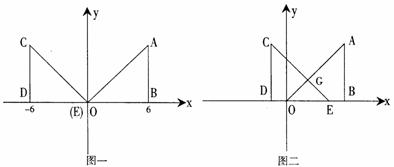
与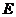 重合.
重合.
(1)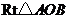 固定不动,
固定不动,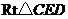 沿
沿 轴以每秒2个单位长度的速度向右运动,当点
轴以每秒2个单位长度的速度向右运动,当点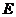 运动到与点
运动到与点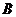 重合时停止,设运动
重合时停止,设运动 秒后,
秒后,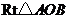 和
和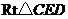 的重叠部分面积为
的重叠部分面积为 ,求
,求 与
与 之间的函数关系式;
之间的函数关系式;
(2)当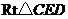 以(1)中的速度和方向运动,运动时间
以(1)中的速度和方向运动,运动时间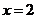 秒时,
秒时, 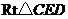 运动到如图二所示的位置,若抛物线
运动到如图二所示的位置,若抛物线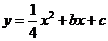 过点
过点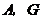 ,求抛物线的解析式;
,求抛物线的解析式;
(3)现有一动点 在(2)中的抛物线上运动,试问点
在(2)中的抛物线上运动,试问点 在运动过程中是否存在点
在运动过程中是否存在点 到
到 轴或
轴或 轴的距离为2的情况,若存在,请求出点
轴的距离为2的情况,若存在,请求出点 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com