
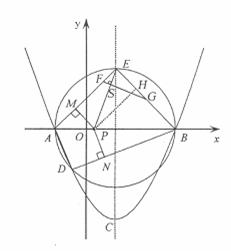
20. 解:(1)设AB的函数表达式为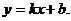
∵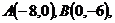 ∴
∴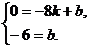 ∴
∴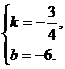
∴直线AB的函数表达式为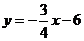 .
.
(2)设抛物线的对称轴与⊙M相交于一点,依题意知这一点就是抛物线的顶点C。又设对称轴与 轴相交于点N,在直角三角形AOB中,
轴相交于点N,在直角三角形AOB中,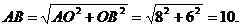
因为⊙M经过O、A、B三点,且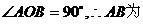 ⊙M的直径,∴半径MA=5,∴N为AO的中点AN=NO=4,∴MN=3∴CN=MC-MN=5-3=2,∴C点的坐标为(-4,2).
⊙M的直径,∴半径MA=5,∴N为AO的中点AN=NO=4,∴MN=3∴CN=MC-MN=5-3=2,∴C点的坐标为(-4,2).
设所求的抛物线为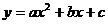
则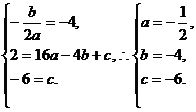
∴所求抛物线为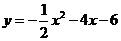
(3)令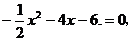 得D、E两点的坐标为D(-6,0)、E(-2,0),所以DE=4.
得D、E两点的坐标为D(-6,0)、E(-2,0),所以DE=4.
又AC=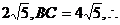 直角三角形的面积
直角三角形的面积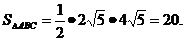
假设抛物线上存在点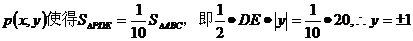 .
.
当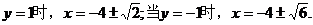 故满足条件的存在.它们是
故满足条件的存在.它们是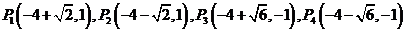 .
.
19. 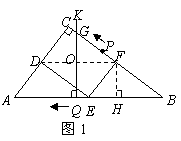 解:(1)25.
解:(1)25.
(2)能.
如图,连结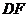 ,过点
,过点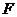 作
作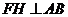 于点
于点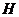 ,
,
由四边形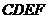 为矩形,可知
为矩形,可知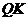 过
过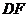 的中点
的中点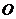 时,
时,
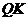 把矩形
把矩形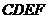 分为面积相等的两部分
分为面积相等的两部分
(注:可利用全等三角形借助割补法或用中心对称等方法说明),
 此时
此时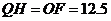 .由
.由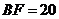 ,
,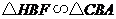 ,得
,得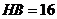 .
.
故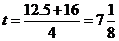 .
.
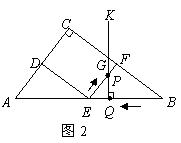
(3)①当点 在
在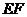 上
上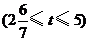 时,如图2.
时,如图2.
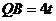 ,
,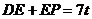 ,
,
 由
由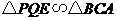 ,得
,得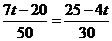 .
.
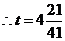 .
.
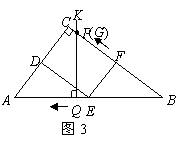
②当点 在
在 上
上 时,如图3.
时,如图3.
 已知
已知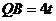 ,从而
,从而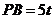 ,
,
由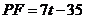 ,
,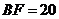 ,得
,得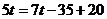 .
.
解得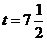 .
.
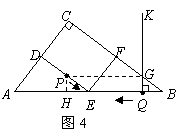
(4)如图4,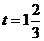 ;如图9,
;如图9,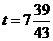 .
.
 (注:判断
(注:判断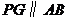 可分为以下几种情形:当
可分为以下几种情形:当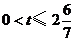 时,点
时,点 下行,点
下行,点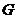 上行,可知其中存在
上行,可知其中存在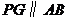 的时刻,如图8;此后,点
的时刻,如图8;此后,点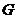 继续上行到点
继续上行到点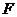 时,
时,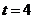 ,而点
,而点 却在下行到点
却在下行到点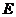 再沿
再沿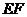 上行,发现点
上行,发现点 在
在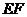 上运动时不存在
上运动时不存在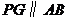 ;当
;当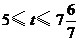 时,点
时,点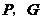 均在
均在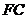 上,也不存在
上,也不存在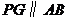 ;由于点
;由于点 比点
比点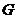 先到达点
先到达点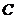 并继续沿
并继续沿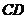 下行,所以在
下行,所以在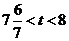 中存在
中存在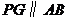 的时刻,如图5;当
的时刻,如图5;当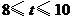 时,点
时,点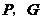 均在
均在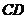 上,不存在
上,不存在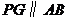 )
)
18. 解:(1)由题意得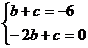 解得b=-2,c=-4
解得b=-2,c=-4
∴此抛物线的解析式为:y=x2-2x-4
2(2)由题意得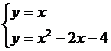
解得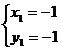
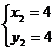
∴点B的坐标为(4,4)
将x=m代入 y=x条件得y=m
∴点N的坐标为(m , m)
同理点M的坐标为(m , m2-2m-4 ),点P的坐标为(m , 0 )
∴PN=|m| ,MP=| m2-2m-4 |
∵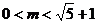
∴MN=PN+MP=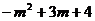
(3)作BC⊥MN于点C ,则BC=4-m ,OP=m
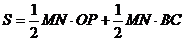 =
=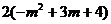 =
=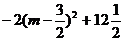
∵-2<0
∴当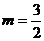 时,S有最大值
时,S有最大值
17.
解:⑴对称轴是直线: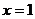 ,点B的坐标是(3,0).
,点B的坐标是(3,0).
⑵如图,连接PC,∵点A、B的坐标分别是A(-1,0)、B (3,0),
∴AB=4.∴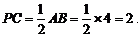
在Rt△POC中,∵OP=PA-OA=2-1=1,
∴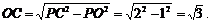
∴b=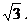
当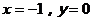 时,
时,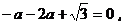
∴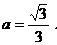
∴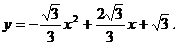
⑶存在.
理由:如图,连接AC、BC.设点M的坐标为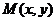 .
.
①当以AC或BC为对角线时,点M在x轴上方,此时CM∥AB,且CM=AB.
由⑵知,AB=4,∴|x|=4,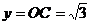 .
.
∴x=±4.∴点M的坐标为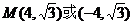 .
.
②当以AB为对角线时,点M在x轴下方.
过M作MN⊥AB于N,则∠MNB=∠AOC=90°.
∵四边形AMBC是平行四边形,∴AC=MB,且AC∥MB.
∴∠CAO=∠MBN.∴△AOC≌△BNM.∴BN=AO=1,MN=CO=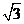 .
.
∵OB=3,∴0N=3-1=2.
∴点M的坐标为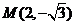 .
.
综上所述,坐标平面内存在点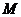 ,使得以点A、B、C、M为顶点的四边形是平行四边形.其坐标为
,使得以点A、B、C、M为顶点的四边形是平行四边形.其坐标为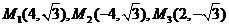 .
.
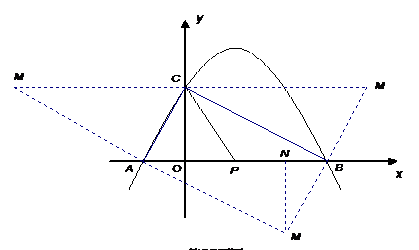
16. (1)由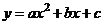 ,则得
,则得
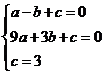 ,解得
,解得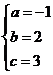
故函数解析式是: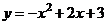 。
。
由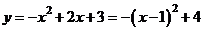 知,
知,
点M(1,4)。
(2)由点E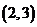 在正比例函数
在正比例函数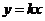 的图像上得,
的图像上得,
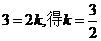 ,故
,故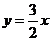 ,
,
由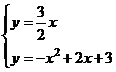 解得D点坐标为(
解得D点坐标为(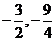 ),
),
由图象可知,当二次函数的函数值大于正比例函数时,自变量 的取值范围是
的取值范围是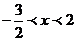 。
。
(3)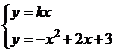
解得,点D、E坐标为D(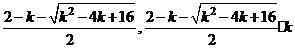 )、
)、
E(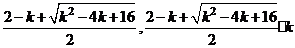 ),
),
则点P坐标为P(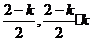 )由
)由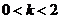 ,知点P在第一象限。
,知点P在第一象限。
由点B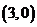 ,C
,C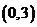 ,M(1,4),得
,M(1,4),得
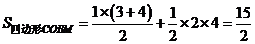 ,
,
则
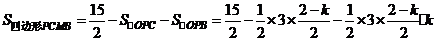
整理,配方得
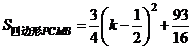 。
。
故当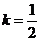 时,四边形PCMB的面积值最小,最小值是
时,四边形PCMB的面积值最小,最小值是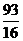 。
。
15. 解:(1)将y=0代入y=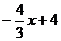 ,得到x=3,∴点B的坐标为(3,0);
,得到x=3,∴点B的坐标为(3,0);
将x=0,代入y=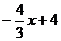 ,得到y=4, ∴点C的坐标为(0,4)
,得到y=4, ∴点C的坐标为(0,4)
在Rt△OBC中,∵OC=4,OB=3,∴BC=5。
又A(-2,0),∴AB=5,∴AB=BC,∴△ABC是等腰三角形。
(2)∵AB=BC=5,故点M、N同时开始运动,同时停止运动。
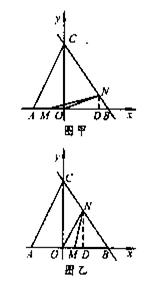 过点N作ND⊥x轴于D ,
过点N作ND⊥x轴于D ,
则ND=NB●sin∠OBC=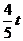 ,
,
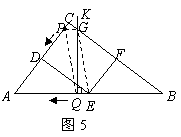
当0<t<2时(如图甲)
OM=2-t,
∴s=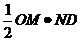 =
=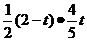
=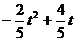
当2<t≤5时(如图乙),OM=t-2,
∴s=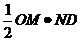 =
=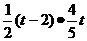
=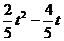
(注:若将t的取值范围分别写为0≤t≤2和2≤t≤5,不扣分)
存在s=4的情形。
当s=4时,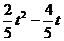 =4
=4
解得t1=1+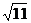 , t2=1-
, t2=1-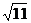 秒。
秒。
当MN⊥x轴时,△MON为直角三角形,
MB=NB●COS∠MBN=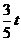 ,又MB=5-t.
,又MB=5-t.
∴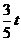 =5-t, ∴t=
=5-t, ∴t=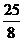
当点M,N分别运动到点B,C时,△MON为直角三角形,t=5.
故△MON为直角三角形时,t=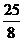 秒或t=5秒
秒或t=5秒
14. .解:(1) ∵四边形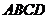 为正方形 ∴
为正方形 ∴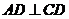
∵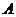 、
、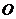 、
、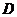 在同一条直线上 ∴
在同一条直线上 ∴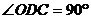 ∴直线
∴直线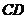 与⊙
与⊙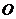 相切;
相切;
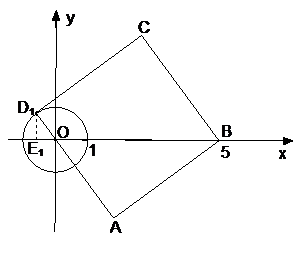 (2)直线
(2)直线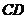 与⊙
与⊙ 相切分两种情况:
相切分两种情况:
①如图1, 设 点在第二象限时,过
点在第二象限时,过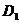 作
作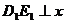 轴于点
轴于点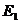 ,设此时的正方形的边长为
,设此时的正方形的边长为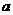 ,则
,则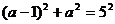 ,解得
,解得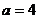 或
或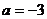 (舍去).
(舍去).
由 ∽
∽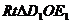 得
得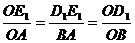
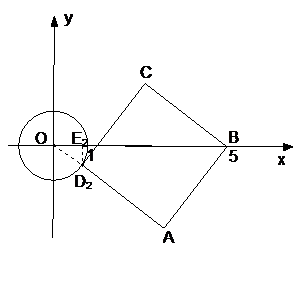 ∴
∴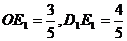 ∴
∴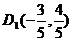 ,故直线
,故直线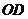 的函数关系式为
的函数关系式为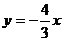 ;
;
②如图2, 设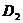 点在第四象限时,过
点在第四象限时,过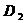 作
作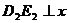 轴于点
轴于点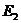 ,设此时的正方形的边长为
,设此时的正方形的边长为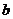 ,则
,则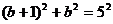 ,解得
,解得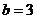 或
或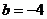 (舍去).
(舍去).
由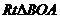 ∽
∽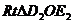 得
得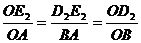
∴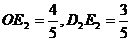 ∴
∴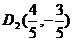 ,故直线
,故直线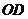 的函数关系式为
的函数关系式为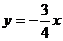 .
.
(3)设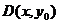 ,则
,则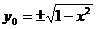 ,由
,由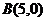 得
得
∴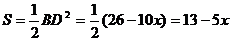
∵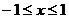
∴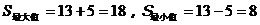 .
.
13. (1)设抛物线解析式为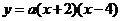 ,把
,把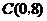 代入得
代入得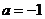 .
.
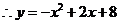
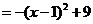 ,
,
顶点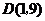 (2分)
(2分)
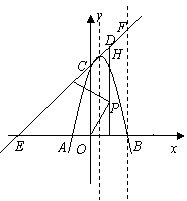
(2)假设满足条件的点 存在,依题意设
存在,依题意设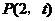 ,
,
由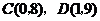 求得直线
求得直线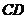 的解析式为
的解析式为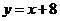 ,
,
它与 轴的夹角为
轴的夹角为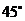 ,设
,设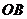 的中垂线交
的中垂线交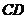 于
于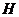 ,则
,则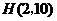 .
.
则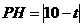 ,点
,点 到
到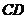 的距离为
的距离为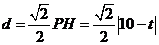 .
.
又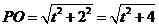 . (4分)
. (4分)
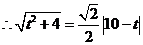 .
.
平方并整理得: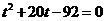
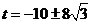 .
.
 存在满足条件的点
存在满足条件的点 ,
, 的坐标为
的坐标为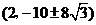 . (6分)
. (6分)
(3)由上求得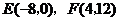 .
.
①若抛物线向上平移,可设解析式为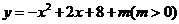 .
.
当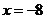 时,
时,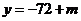 .
.
当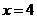 时,
时,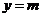 .
.
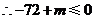 或
或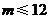 .
.
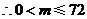 . (8分)
. (8分)
②若抛物线向下移,可设解析式为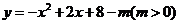 .
.
由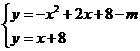 ,
,
有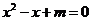 .
.
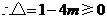 ,
,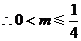 .
.
 向上最多可平移72个单位长,向下最多可平移
向上最多可平移72个单位长,向下最多可平移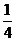 个单位长. (10分
个单位长. (10分
12. 解:(1)设抛物线的解析式为y=a(x-1)2-3……1分
将A(-1,0)代入:0= a(-1-1)2-3,解得a=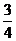 ……2分
……2分
所以,抛物线的解析式为y=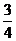 (x-1)2-3,即y=
(x-1)2-3,即y=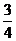 x2-
x2-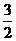 x-
x-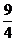 ……3分
……3分
(2)是定值,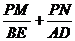 =1……4分
=1……4分
∵AB为直径,∴∠AEB=90°,∵PM⊥AE,∴PM∥BE,∴△APM∽△ABE,所以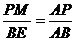 ①
①
同理: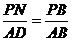 ②……5分
②……5分
①+②: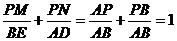 ……6分
……6分
(3)∵直线EC为抛物线对称轴,∴EC垂直平分AB,
∴EA=EB,
∵∠AEB=90°,
∴△AEB为等腰直角三角形,
∴∠EAB=∠EBA=45°……7分
如图,过点P作PH⊥BE与H,
由已知及作法可知,四边形PHEM是矩形.
∴PH=ME且PH∥ME.
在△APM和△PBH中,∵∠AMP=∠PBH=90°,∠EAB=∠BPH=45°,
∴PH=BH,且△APM∽△PBH,
∴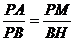 ,∴
,∴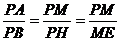 ①……8分
①……8分
在△MEP和△EGF中,∵PE⊥FG,∴∠FGE+∠SEG=90°,
∵∠MEP+∠SEG=90°,∴∠FGE=∠MEP,
∵∠MPE=∠FEG=90°,∴△MEP∽△EGF,
∴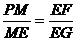 ②
②
由①、②知: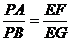 ……9分
……9分
(本题若按分类证明,只要合理,可给满分)
11. 解:(1)900;…………………………………………………………1分
(2)图中点B的实际意义是:当慢车行驶4h时,慢车和快车相遇. ……………2分
(3)由图像可知,慢车12h行驶的路程为900km,所以慢车的速度为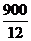 =75(km/h),3分
=75(km/h),3分
当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为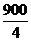 =225(km/h),所以快车的速度为150 km/h.…………………………4分
=225(km/h),所以快车的速度为150 km/h.…………………………4分
(4)根据题意,快车行驶900km到达乙地,所以快车行驶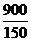 =6(h)到达乙地,此时两车之间的距离为6×75=450(km),
=6(h)到达乙地,此时两车之间的距离为6×75=450(km),
所以点C的坐标为(6,450).
设线段BC所表示的y与x之间的函数关系式为y=kx+b,将(4,0),(6,450)代入得
 0=4k+b
k=225,
0=4k+b
k=225,
解得
450=6k+b b=-900.
所以,线段BC所表示的y与x之间的函数关系式为y=225x-900. ………………6分
自变量x的取值范围是4≤x≤6. …………………………………………7分
(5)慢车与第一辆快车相遇30分钟后与第二辆快车相遇,此时,慢车的行驶时间是4.5h,把x=4.5代入y=225x-900,得y=112.5.此时,慢车和第一列快车之间的距离等于两列快车之间的距离是112.5km,所以两列快车出发的间隔时间是112.5÷150=0.75(h),即第二辆快车比第一辆快车晚出发0.75h. ……………………………………………………………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com