
6.若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为
A. 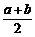 B.
B. 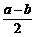 C.
C.
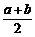 或
或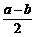 D. a+b或a-b
D. a+b或a-b
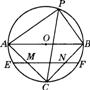
5.如图,⊙0的直径AB=8,P是上半圆(A、B除外)上任一点,∠APB的平分线交⊙O于C,弦EF过AC、BC的中点M、N,则EF的长是( ).
 A.4
A.4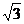 B.2
B.2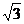 C.6 D.2
C.6 D.2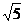
4.已知两圆的半径分别是2和3,两圆的圆心距是4,则这两个圆的位置关系是 ( )
A.外离 B.外切 C.相交 D.内切
3.在半径为1的⊙O中,120º的圆心角所对的弧长是( )
A.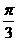 B.
B.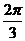 C.
C.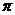 D.
D.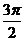
2.已知O为△ABC的外心,∠A=60°,则∠BOC的度数是( )
A.外离 B.外切 C.相交 D.内切
1.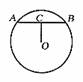 如图,在半径为5的⊙O中,如果弦AB的长为8,那么它的弦心距OC等于( )
如图,在半径为5的⊙O中,如果弦AB的长为8,那么它的弦心距OC等于( )
A. 2 B. 3 C. 4 D. 6
在用放缩法证明不等式时,有时需要“舍掉几个正项”以便达到目的。就是说,如果在和式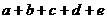 里
里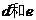 都是正数,可以舍掉
都是正数,可以舍掉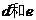 ,从而得到一个明显成立的不等式
,从而得到一个明显成立的不等式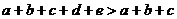 .
.
例如,对于任何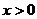 和任何正整数
和任何正整数 ,由二项式定理可得
,由二项式定理可得
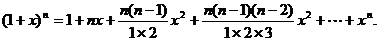
舍掉等式右边第三项及其以后的各项,可以得到不等式: 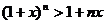 .
.
在后面章节的学习中,我们将会用数学归纳法证明这一不等式的正确性。该不等式不仅当 是正整数的时候成立,而且当
是正整数的时候成立,而且当 是任何大于1的有理数的时候也成立。这就是著名的贝努利不等式。
是任何大于1的有理数的时候也成立。这就是著名的贝努利不等式。
在今后的学习中,可以利用微积分证明更一般的贝努利不等式:设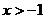 ,则在
,则在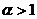 或
或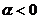 时,
时,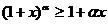 ,在
,在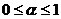 时,
时,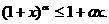
4、其推广形式 ,设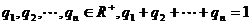 ,
,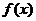 是[a,b]上的凸函数,则对任意
是[a,b]上的凸函数,则对任意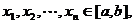 有
有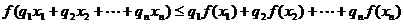 ,
,
当且仅当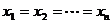 时等号成立。
时等号成立。
若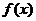 是凹函数,则上述不等式反向。该不等式称为琴生(Jensen)不等式。把琴生不等式应用于一些具体的函数,可以推出许多著名不等式。
是凹函数,则上述不等式反向。该不等式称为琴生(Jensen)不等式。把琴生不等式应用于一些具体的函数,可以推出许多著名不等式。
3、更为一般的情况是:设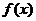 是定义在区间[a,b]上的函数,如果对于[a,b]上的任意两点
是定义在区间[a,b]上的函数,如果对于[a,b]上的任意两点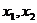 ,有
,有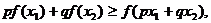
其中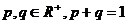 ,则称
,则称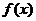 是区间[a,b]上的凸函数。如果不等式反向,即有
是区间[a,b]上的凸函数。如果不等式反向,即有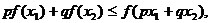 则称
则称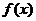 是[a,b]上的凹函数。
是[a,b]上的凹函数。
2、其推广形式是:若函数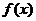 的是[a,b]上的凸函数,则对[a,b]内的任意数
的是[a,b]上的凸函数,则对[a,b]内的任意数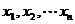 ,都有
,都有
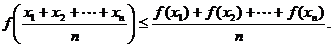 (2)
(2)
当且仅当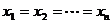 时等号成立。一般称(2)式为琴生不等式。
时等号成立。一般称(2)式为琴生不等式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com