
1、梭伦改革并没有实现雅典公民的完全平等,主要是因为
A、用财产的不平等代替了出身的不平等
B、不同等级的公民享有不同的政治权力利
C、不同等级的公民承担的义务也不相同
D、梭伦改革仅适应了奴隶主阶级的需要
56. 解:(1)由题意知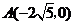 ,
,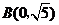 ,
,
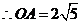 ,
,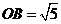 ,
,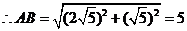 .
.
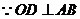 ,
,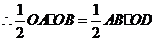
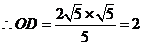 1分
1分
 过点
过点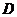 作
作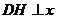 轴于点
轴于点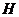 (如图1)
(如图1)
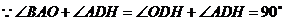 ,
,
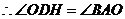 ,
,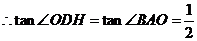 ,
,
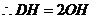 .
.
设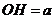 ,则
,则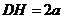 ,
,
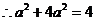 ,
,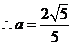 .
.

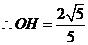 ,
,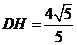 ,
,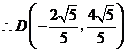 1分
1分
(2)设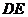 与
与 轴交于点
轴交于点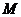 (如图2)
(如图2)
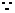 四边形
四边形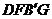 是平行四边形,
是平行四边形,
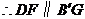 ,
,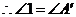 .
.
又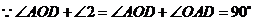 ,
,
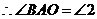 .
.
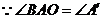 ,
,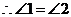 ,
,
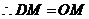 1分
1分
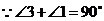 ,
,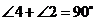 ,
,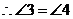 .
.
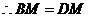 ,
,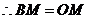 .
.
 点
点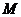 是
是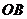 中点,
中点,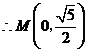 1分
1分
设线段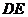 所在直线解析式为
所在直线解析式为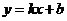 .
.
把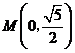 ,
,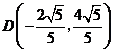 代入
代入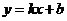 ,
,
得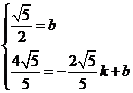 解得
解得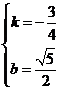 .
.
 线段
线段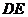 所在直线的解析式为
所在直线的解析式为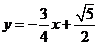 1分
1分
(3)设直线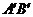 交
交 轴于点
轴于点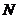 (如图3),过点
(如图3),过点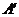 作
作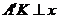 轴于点
轴于点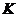 .
.
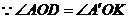 ,
,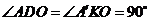 ,
,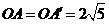 ,
,
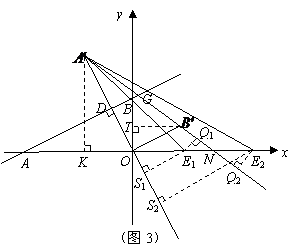
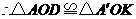 ,
,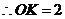 ,
,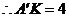 ,
,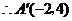 .
.
过点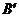 作
作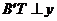 轴于点
轴于点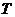 ,
,
同理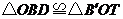 ,
,
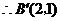 .
.
设直线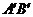 的解析式为
的解析式为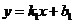 ,
,
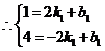 ,解得
,解得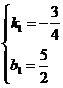 .
.
 直线
直线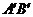 的解析式为
的解析式为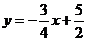 1分
1分
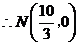 ,
,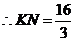 ,
,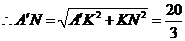 .
.
当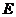 点在
点在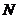 点左侧点
点左侧点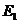 位置时,过点
位置时,过点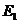 作
作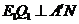 于点
于点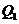 .
.
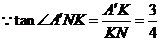 ,
, 设
设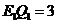 m,则
m,则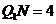 m.
m.
又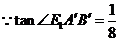 ,
,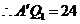 m,
m,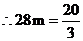 .
.
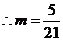 ,
,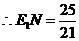 ,
,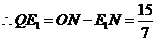 ,此时
,此时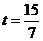 1分
1分
过点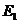 作
作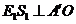 于点
于点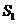 .
.
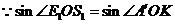 ,
,
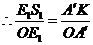 ,
,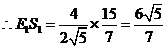 .
.
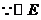 的半径为
的半径为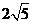 ,而
,而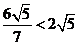 ,
,
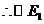 与直线
与直线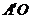 相交. 1分
相交. 1分
当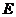 点在
点在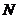 点右侧点
点右侧点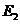 位置时
位置时
过点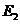 作
作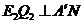 于点
于点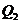
同理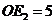 此时
此时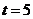 1分
1分
过点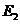 作
作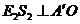 于点
于点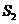
同理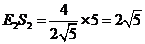 .
.
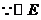 的半径为
的半径为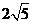 ,
,
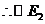 与直线
与直线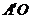 相切 1分
相切 1分
 当
当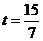 或
或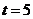 时,
时,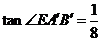 ;
;
当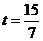 时直线
时直线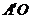 与
与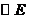 相交,当
相交,当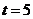 时直线
时直线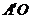 与
与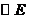 相切.
相切.
55. 解:(1)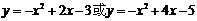 等
(满足条件即可)
等
(满足条件即可)
(2)设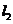 的解析式为
的解析式为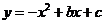 ,联立方程组
,联立方程组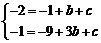 ,
,
解得: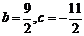 ,则
,则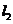 的解析式为
的解析式为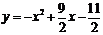 ,
,
点C的坐标为(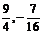 )
)
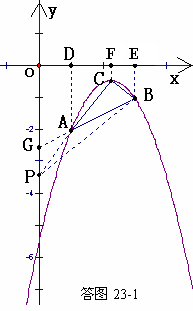
(3)如答图23-1,过点A、B、C三点分别作x轴的垂线,垂足分别为D、E、F,则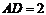 ,
,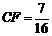 ,
,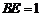 ,
,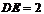 ,
,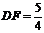 ,
,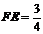 .
.
得: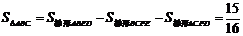 .
.
延长BA交y轴于点G,直线AB的解析式为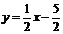 ,则点G的坐标为(0,
,则点G的坐标为(0,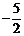 ),设点P的坐标为(0,
),设点P的坐标为(0,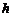 )
)
①当点P位于点G的下方时,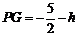 ,连结AP、BP,则
,连结AP、BP,则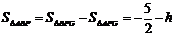 ,又
,又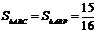 ,得
,得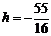 ,点P的坐标为(0,
,点P的坐标为(0,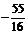 ).
…… 6分
).
…… 6分
②当点P位于点G的上方时,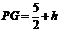 ,同理
,同理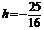 ,点P的坐标为(0,
,点P的坐标为(0,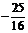 ).
).
综上所述所求点P的坐标为(0,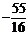 )或(0,
)或(0,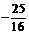 )
)
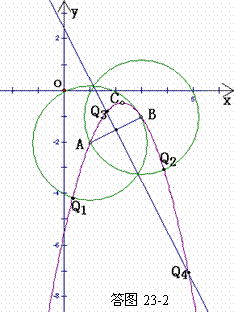
(4) 作图痕迹如答图23-2所示.
 由图可知,满足条件的点有
由图可知,满足条件的点有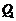 、
、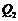 、
、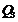 、
、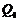 ,共4个可能的位置.
,共4个可能的位置.
54. (1)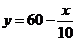 .
.
(2)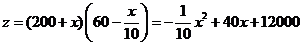
(3)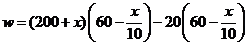
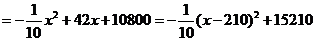
当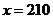 时,
时,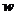 有最大值.
有最大值.
此时,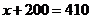 ,就是说,当每个房间的定价为每天410元时,
,就是说,当每个房间的定价为每天410元时,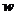 有最大值,且最大值是15210元.
有最大值,且最大值是15210元.
53. 解:(1)设直线BC的解析式为y=kx+b 依题意得:
 4=k×0+4
4=k×0+4
10=8k+b
解之得:k= 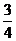 ; b=
4
; b=
4
所以直线BC的解析式为y=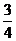 x+4
x+4
t=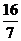
s= t (8>t>0)
t (8>t>0)
s=44-2x (18>x≥8)
s=-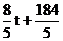
(4)不存在。理由如下:过C作CM⊥AB于M,易知CM=OA=8
AM=OC=4,所以BM=6.假设四边形CQPD为矩形,则PQ=CD=5,PQ‖CD,
根据Rt△PAQ∽ Rt△BDP可求PB=5,PB=PD,这与三角形PBD是直角三角形相矛盾,所以假设不成立在OA上不存在点Q,,使四边形CQPD为矩形
52.
(1)证明:设E(x1,y1),F(x2,y2),△AOE和△FOB的面积为S1、S2
由题意得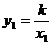 ,
,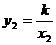
∴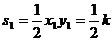
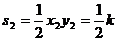
∴S1=S2 ,即△AOE和△FOB的面积相等
(2)由题意知:E、F两点坐标分别为E(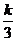 ,3)、F(4,
,3)、F(4,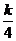 )
)
S△ECF=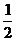 EC·CF=
EC·CF=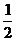 (4-
(4-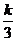 )(3-
)(3-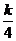 )
)
S△EDF=S矩形AOBC-S△AOE-S△ECF=12-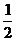 k-
k-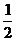 k-S△ECF
k-S△ECF
S=S△OEF-S△ECF=12-k-2 S△ECF=12-k-2×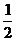 (4-
(4-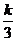 )(3-
)(3-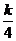 )
)
S=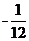 k2+k
k2+k
当k=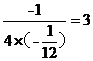
(3)解:设存在这样的点F,将△CEF沿EF对折后,C点恰好落在OB边上的M点,过点E作EN⊥OB,垂足为N
由题意得:EN=AO=3,EM=EC=4-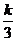 ,MF=CF=3-
,MF=CF=3-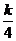
∵FMN+FMB=FMB+MFB=90,∴EMN=MFB
又∵ENM=MBF=90
∴△ENM△MBF
∴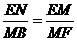 ∴
∴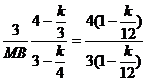
∴MB=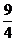
∵MB2+BF2=MF2 ∴ (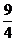 )2+(
)2+(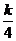 )2=(3-
)2=(3-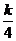 )2
)2
解得 k=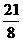
∴BF=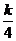 =
=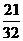
51. 解:
(1)①CF与BD位置关系是 垂 直、数量关系是相 等;
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得 AD=AF ,∠DAF=90º.
∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC,
又AB=AC ,∴△DAB≌△FAC , ∴CF=BD
∠ACF=∠ABD.
∵∠BAC=90º, AB=AC ,∴∠ABC=45º,∴∠ACF=45º,
∴∠BCF=∠ACB+∠ACF= 90º.即 CF⊥BD

(2)画图正确
当∠BCA=45º时,CF⊥BD(如图丁).
理由是:过点A作AG⊥AC交BC于点G,∴AC=AG
可证:△GAD≌△CAF ∴∠ACF=∠AGD=45º
∠BCF=∠ACB+∠ACF= 90º. 即CF⊥BD
(3)当具备∠BCA=45º时,
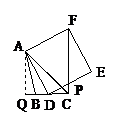
过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)
∵DE与CF交于点P时, ∴此时点D位于线段CQ上,
∵∠BCA=45º,可求出AQ= CQ=4.设CD=x ,∴ DQ=4-x,
容易说明△AQD∽△DCP,∴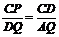 , ∴
, ∴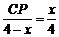 ,
,
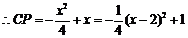 .
.
∵0<x≤3 ∴当x=2时,CP有最大值1.
50.
解:(1)AD=4;
(2)x=2.4;
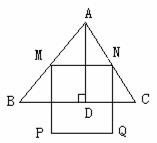
(3)设BC分别交MP、NQ于E、F,则四边形MEFN为矩形。
设ME=FN=h,AD交MN于G(如图2),GD=NF=h,AG=4-h
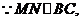
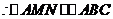
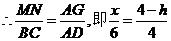
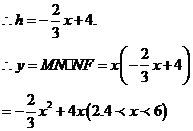
配方得: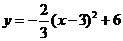 ,所以当x=3时,y有最大值,最大值是6。
,所以当x=3时,y有最大值,最大值是6。
49. 解:(1)∵四边形OABC为矩形,
∴∠CDE=∠AOE=90°,OA=BC=CD
又∵∠CED=∠OEA,∴△CDE≌△AOE
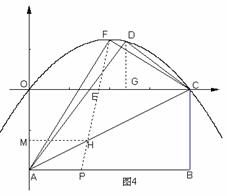 ∴OE=DE.
∴OE=DE.
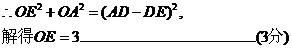
EC=8-3=5.如图4,过点D作DG⊥EC于G,
∴△DGE∽△CDE
∴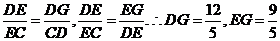
∴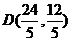
∵O点为坐标原点,故设过O、C、D三点抛物线的解析式为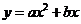 .
.
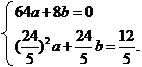
∴
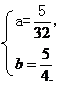
解得
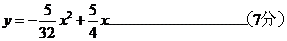
因为抛物线的对称轴为x=4,∴
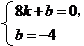
设直线AC的解析式为y=kx+b,则
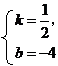
解得
∴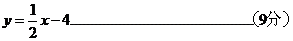
设直线EP交直线AC于H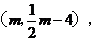 过H作HM⊥OA于M.
过H作HM⊥OA于M.
∴△AMH∽△AOC.∴HM:OC=AH:AC.
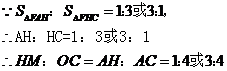
∴HM=2或6,即m=2或6

说明:只求对一个值的给11分。
48.
提示:
⑴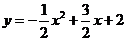 ;⑵
;⑵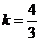 ;⑶M(3,2),N(1,3)
;⑶M(3,2),N(1,3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com