
37.
解:(1)依题意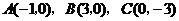 分别代入
分别代入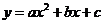 1分
1分
解方程组得所求解析式为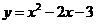 4分
4分
(2)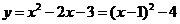 5分
5分
 顶点坐标
顶点坐标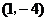 ,对称轴
,对称轴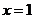 7分
7分
(3)设圆半径为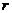 ,当
,当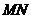 在
在 轴下方时,
轴下方时, 点坐标为
点坐标为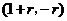 8分
8分
把 点代入
点代入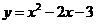 得
得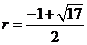 9分
9分
同理可得另一种情形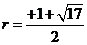
 圆的半径为
圆的半径为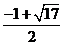 或
或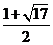
36. 解:(1)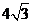 ,
,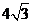 ,
,
等腰;
(2)共有9对相似三角形.
①△DCE、△ABE与△ACD或△BDC两两相似,分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对)
②△ABD∽△EAD,△ABD∽△EBC;(有2对)
③△BAC∽△EAD,△BAC∽△EBC;(有2对)
所以,一共有9对相似三角形.
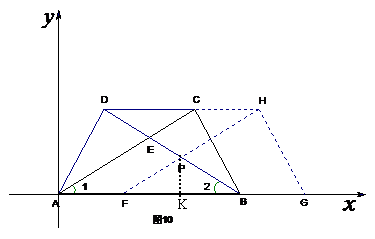
(3)由题意知,FP∥AE,
∴ ∠1=∠PFB,
又∵ ∠1=∠2=30°,
∴ ∠PFB=∠2=30°,
∴ FP=BP
过点P作PK⊥FB于点K,则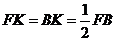 .
.
∵ AF=t,AB=8,
∴ FB=8-t,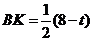 .
.
在Rt△BPK中,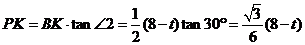 .
.
∴ △FBP的面积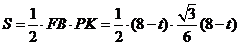 ,
,
∴ S与t之间的函数关系式为:
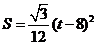 ,或
,或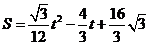 .
.
t的取值范围为: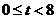 .
.
35.
解:(1)设正方形的边长为 cm,则
cm,则
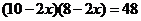 .
.
即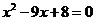 .
.
解得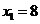 (不合题意,舍去),
(不合题意,舍去),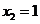 .
.
 剪去的正方形的边长为1cm.
剪去的正方形的边长为1cm.
(注:通过观察、验证直接写出正确结果给3分)
(2)有侧面积最大的情况.
设正方形的边长为 cm,盒子的侧面积为
cm,盒子的侧面积为 cm2,
cm2,
则 与
与 的函数关系式为:
的函数关系式为:
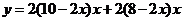 .
.
即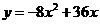 .
.
改写为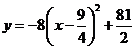 .
.
 当
当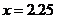 时,
时,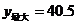 .
.
即当剪去的正方形的边长为2.25cm时,长方体盒子的侧面积最大为40.5cm2.
 (3)有侧面积最大的情况.
(3)有侧面积最大的情况.
设正方形的边长为 cm,盒子的侧面积为
cm,盒子的侧面积为 cm2.
cm2.
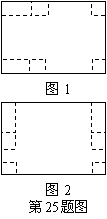
若按图1所示的方法剪折,则 与
与 的函数关系式为:
的函数关系式为:
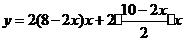 .
.
即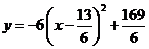 .
.
 当
当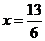 时,
时,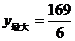 .
.
若按图2所示的方法剪折,则 与
与 的函数关系式为:
的函数关系式为:
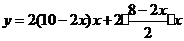 .
.
即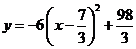 .
.
 当
当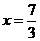 时,
时,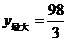 .
.
比较以上两种剪折方法可以看出,按图2所示的方法剪折得到的盒子侧面积最大,即当剪去的正方形的边长为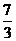 cm时,折成的有盖长方体盒子的侧面积最大,最大面积为
cm时,折成的有盖长方体盒子的侧面积最大,最大面积为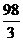 cm2.
cm2.
34. 解:(1)∵当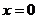 和
和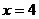 时,
时, 的值相等,∴
的值相等,∴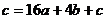 ,
,
∴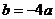 ,∴
,∴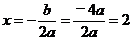
将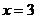 代入
代入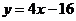 ,得
,得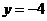 ,
,
将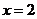 代入
代入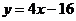 ,得
,得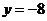
∴设抛物线的解析式为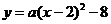
将点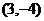 代入,得
代入,得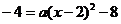 ,解得
,解得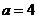 .
.
∴抛物线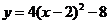 ,即
,即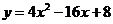
(2)设直线OM的解析式为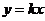 ,将点M
,将点M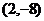 代入,得
代入,得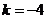 ,
,
∴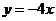
则点P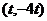 ,
,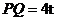 ,而
,而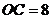 ,
,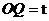 .
.
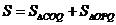 =
=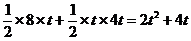
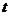 的取值范围为:
的取值范围为: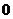 <
<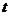 ≤
≤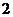
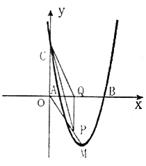
(3)随着点 的运动,四边形
的运动,四边形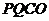 的面积
的面积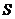 有最大值.
有最大值.
从图像可看出,随着点 由
由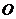 →
→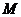 运动,
运动,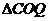 的面积与
的面积与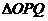 的面积在不断增大,即
的面积在不断增大,即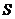 不断变大,显当然点
不断变大,显当然点 运动到点
运动到点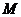 时,
时,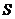 最值
最值
此时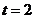 时,点
时,点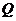 在线段
在线段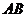 的中点上
的中点上
因而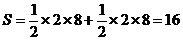 .
.
当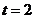 时,
时,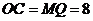 ,
,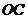 ∥
∥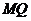 ,∴四边形
,∴四边形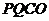 是平行四边形.
是平行四边形.
(4)随着点 的运动,存在
的运动,存在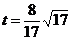 ,能满足
,能满足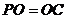
设点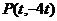 ,
,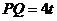 ,
,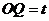 . 由勾股定理,得
. 由勾股定理,得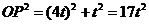 .
.
∵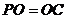 ,∴
,∴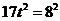 ,
,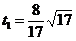 <
<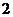 ,
,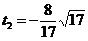 (不合题意)
(不合题意)
∴当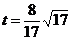 时,
时,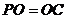
33. 解:(1)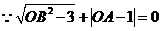
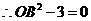 ,
,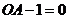 (1分)
(1分)
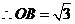 ,
,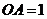
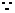 点
点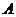 ,点
,点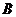 分别在
分别在 轴,
轴, 轴的正半轴上
轴的正半轴上
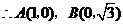 (2分)
(2分)
(2)求得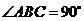 (3分)
(3分)
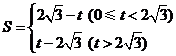
(每个解析式各1分,两个取值范围共1分) (6分)
(3)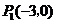 ;
;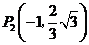 ;
;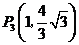 ;
;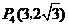 (每个1分,计4分)
(每个1分,计4分)
(10分)
注:本卷中所有题目,若由其它方法得出正确结论,酌情给分.
32. 解:(1) 弦(图中线段AB)、弧(图中的ACB弧)、弓形、求弓形的面积(因为是封闭图形)等.
(写对一个给1分,写对两个给2分)
(2) 情形1 如图21,AB为弦,CD为垂直于弦AB的直径. …………………………3分
结论:(垂径定理的结论之一). …………………………………………………………………………4分
证明:略(对照课本的证明过程给分). ……………………………………………………………7分
情形2 如图22,AB为弦,CD为弦,且AB与CD在圆内相交于点P.
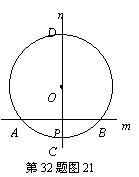 结论:
结论: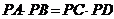 .
.
证明:略.
情形3 (图略)AB为弦,CD为弦,且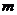 与
与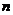 在圆外相交于点P.
在圆外相交于点P.
结论: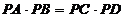 .
.
证明:略.
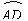
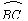 情形4 如图23,AB为弦,CD为弦,且AB∥CD.
情形4 如图23,AB为弦,CD为弦,且AB∥CD.
结论: = .
证明:略.
(上面四种情形中做一个即可,图1分,结论1分,证明3分;
其它正确的情形参照给分;若提出的是错误的结论,则需证明结论是错误的)
(3) 若点C和点E重合,
则由圆的对称性,知点C和点D关于直径AB对称. …………………………………………8分
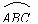 设
设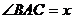 ,则
,则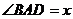 ,
,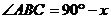 .…………………………………………9分
.…………………………………………9分
又D是 的中点,所以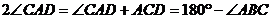 ,
,
即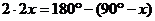 .………………………………………………………………………………10分
.………………………………………………………………………………10分
解得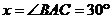 .………………………………………………………………………………………11分
.………………………………………………………………………………………11分
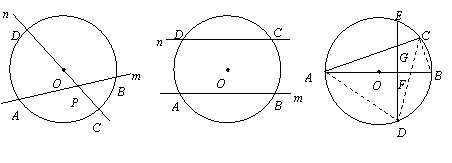 (若求得
(若求得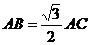 或
或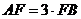 等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明)
等也可,评分可参照上面的标准;也可以先直觉猜测点B、C是圆的十二等分点,然后说明)
31. 解:(1)△BPF-△EBF-△BCD………………2分
以△BPF-△EBF为例,证明如下:
∠BPF=∠EBF=60°
∠BFP=∠BFE
所以 △BPF-△EBF………………4分
(2)均成立,均有△BPF-△EBF-△BCD………………6分
(3)BD平分∠ABC时,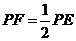 ………………7分
………………7分
证明:∵BD平分∠ABC
∴∠ABP=∠PBF=30°
∴∠BPF=60°
∵∠BFP=90°
∴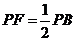 ………………8分
………………8分
又∠BEF=60°-30°=30°=∠ABP
∴BP=EP
∴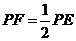 ………………10分
………………10分
注:所有其它解法均酌情赋分.
30. 解:(1)这样的抛物线F是不存在的。
假定这样的抛物线F存在,因为顶点为Q,而且F是由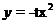 平移的得到的,所以F的关系式为
平移的得到的,所以F的关系式为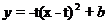 ,化简得
,化简得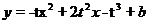
根据二次函数和一元二次方程的关系,函数y图像与x轴的交点B,C的横坐标等于方程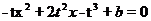 的两个根,设这两个根为x1 ,x2
,则x1·x2=
的两个根,设这两个根为x1 ,x2
,则x1·x2=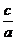 =
=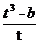 =
=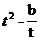 ,
,
∣OA∣2 =t2, ∣OB∣·∣OC∣=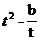 ,若二者相等的话,b=0,这样Q就在x轴上,抛物线F不可能与x轴有两个交点B,C.和假定产生矛盾,所以这样的抛物线F是不存在的。
,若二者相等的话,b=0,这样Q就在x轴上,抛物线F不可能与x轴有两个交点B,C.和假定产生矛盾,所以这样的抛物线F是不存在的。
(2)∵AQ∥BC
∴Q点纵坐标和A点纵坐标相同。
即Q(t,t)
∵tan∠ABO=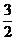 .OA=t
.OA=t
∴OB=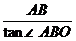 =
=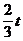
F是由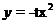 平移得到,顶点为Q(t,t),所以关系式为
平移得到,顶点为Q(t,t),所以关系式为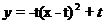
把B点坐标(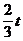 ,0)代入关系式得,
,0)代入关系式得,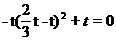 ,解得t1=0(舍去),
,解得t1=0(舍去),
t2=-3(舍去),t3=3,把t=3代入原关系式得抛物线F的关系式为
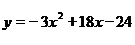
29. 解:(1)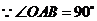 ,
,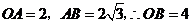 2分
2分
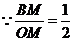 ,
,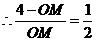 ,
,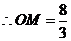 3分
3分
(2)由(1)得: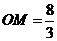 ,
,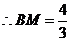 .
.
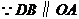 ,易证
,易证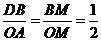 4分
4分
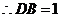 ,
,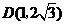 . 5分
. 5分

 过
过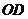 的直线所对应的函数关系式是
的直线所对应的函数关系式是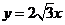 . 6分
. 6分
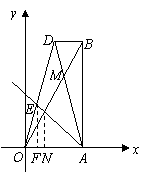
(3)依题意:当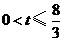 时,
时,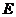 在
在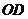 边上,
边上,
分别过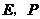 作
作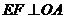 ,
,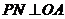 ,垂足分别为
,垂足分别为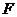 和
和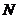 ,
,
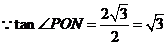 ,
,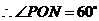 ,
,
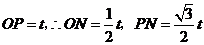 .
.
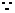 直线
直线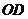 所对应的函数关系式是
所对应的函数关系式是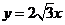 ,
,
 设
设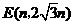 7分
7分
易证得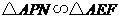 ,
,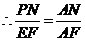 ,
,
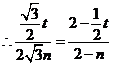 8分
8分
整理得: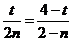
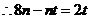 ,
,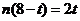 ,
,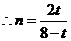 9分
9分
由此,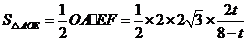 ,
,
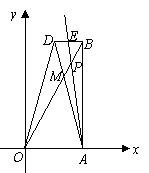
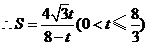 10分
10分
当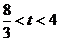 时,点
时,点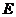 在
在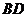 边上,
边上,
此时,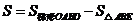 ,
,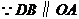 ,
,
易证: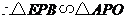
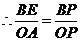 ,
,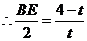
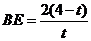 11分
11分
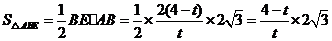
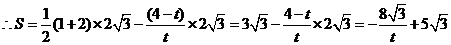 .
.
综上所述: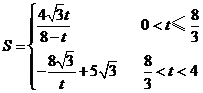 12分
12分
(1)解法2: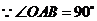 ,
,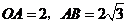 .
.
易求得: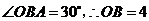 2分
2分
(3)解法2:分别过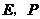 作
作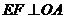 ,
,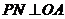 ,垂足分别为
,垂足分别为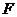 和
和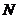 ,
,
由(1)得,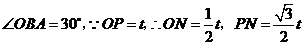 ,
,
即: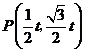 ,又
,又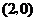 ,
,
设经过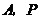 的直线所对应的函数关系式是
的直线所对应的函数关系式是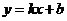
则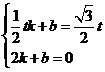 解得:
解得: 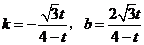 7分
7分
 经过
经过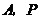 的直线所对应的函数关系式是
的直线所对应的函数关系式是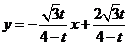 .
.
依题意:当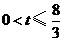 时,
时,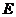 在
在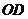 边上,
边上,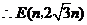 在直线
在直线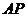 上,
上,
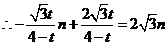 8分
8分
整理得: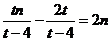
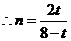 9分
9分
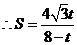 (
(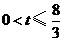 ) 10分
) 10分
当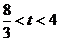 时,点
时,点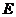 在
在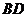 上,此时,点
上,此时,点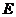 坐标是
坐标是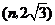 ,因为
,因为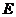 在直线
在直线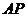 上,
上,
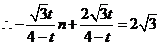
整理得: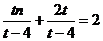 .
.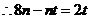 .
.
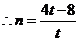 11分
11分
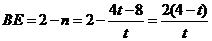
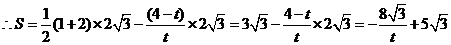
综上所述: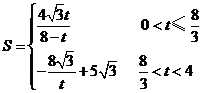 12分
12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com