
2. 定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率
定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率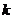 ,即
,即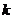 =tan
=tan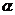 (
(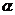 ≠90°);倾斜角为90°的直线没有斜率;
≠90°);倾斜角为90°的直线没有斜率;
定义法:已知直线的倾斜角为α,且α≠90°,则斜率k=tanα.
直线方程法:ax+by+c=0的斜率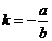 。方向向量法:若a=(m,n)为直线的方向向量,则直线的斜率k=
。方向向量法:若a=(m,n)为直线的方向向量,则直线的斜率k=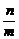 .过两点
.过两点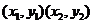 的直线的斜率
的直线的斜率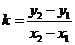 ;求导数;点差法
;求导数;点差法
曲线与方程-应用
1. 直线的倾斜角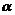 的范围是
的范围是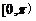
在平面直角坐标系中,对于一条与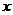 轴相交的直线
轴相交的直线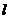 ,如果把
,如果把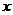 轴绕着交点按逆时针方向转到和直线
轴绕着交点按逆时针方向转到和直线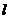 重合时所转的最小正角记为
重合时所转的最小正角记为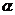 ,那么
,那么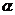 就叫做直线的倾斜角。当直线
就叫做直线的倾斜角。当直线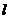 与
与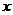 轴重合或平行时,规定倾斜角为0;
轴重合或平行时,规定倾斜角为0;
异面直线所成角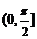 ;直线与平面所成角
;直线与平面所成角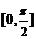 ;二面角和两向量的夹角
;二面角和两向量的夹角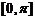 ;平面向量的夹角:
;平面向量的夹角: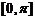 ;直线的倾斜角
;直线的倾斜角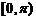 ;
;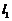 到
到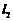 的角
的角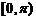 ;
;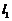 与
与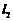 的夹角
的夹角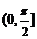 .注意术语:坡度、仰角、俯角、方位角等.
.注意术语:坡度、仰角、俯角、方位角等.
12.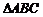 中,易得:
中,易得: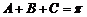 ,
,
①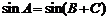 ,
,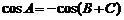 ,
,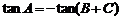 .
.
②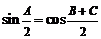 ,
,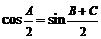 ,
,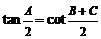 . ③
. ③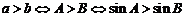
④锐角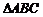 中,
中,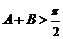 ,
,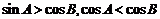 ,
,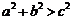 ,类比得钝角
,类比得钝角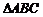 结论.
结论.
⑤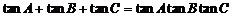 ;
;
高中数学基础知识归类
--献给2009年赣马高级中学高三考生
11.余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍,即
a2=b2+c2-2bccosA; b2=c2+a2-2cacosB; c2=a2+b2-2abcosC
在余弦定理中,令C=90°,这时cosC=0,所以c2=a2+b2.由此可知余弦定理是勾股定理的推广.由①②③可得cosA=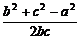 ;cosB=
;cosB=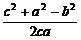 ;cosC=
;cosC=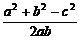 .
.
10.正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即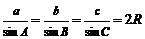
9.三角形中向量性质:
①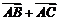 过
过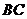 边的中点:
边的中点: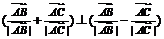 ;
;
②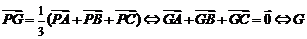 为
为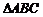 的重心;
的重心;
③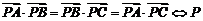 为
为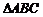 的垂心;
的垂心;
④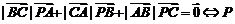
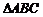 内心;
内心;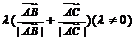 所在直线过
所在直线过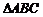 内心.
内心.
⑤设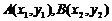 ,
,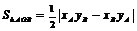 .
. 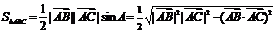 .
.
8.熟记平移公式和定比分点公式.
①当点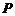 在线段
在线段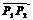 上时,
上时,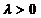 ;当点
;当点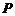 在线段
在线段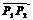 (或
(或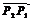 )延长线上时,
)延长线上时,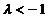 或
或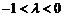 .
.
②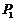 ,
,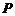 ,
,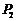 三点共线
三点共线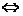 存在实数
存在实数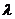 、
、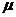 使得
使得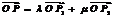 且
且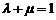 .
.
7.平面向量数量积的坐标表示:⑴若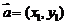 ,
,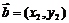 ,则
,则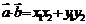 ;
;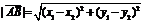 ; ⑵若
; ⑵若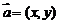 ,则
,则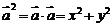 .
.
6. 向量的运算律:(1)交换律: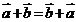 ,
,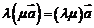 ,
,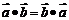 ;
;
(2)结合律: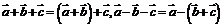 ,
,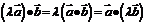 ;
;
(3)分配律: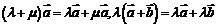 ,
,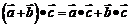 。
。
提醒:(1)向量运算和实数运算有类似的地方也有区别:对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边同乘以一个向量,但不能两边同除以一个向量,即两边不能约去一个向量,切记两向量不能相除(相约);(2)向量的“乘法”不满足结合律,即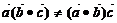
5..运算律:(1)a·b=b·a;(2)(λa)·b=λ(a·b)=a·(λb);(3)(a+b)·c=a·c+b·c.
设a=(x1,y1),b=(x2,y2),则(1)a·b=x1x2+y1y2;(2)|a|=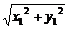 ;(3)cos〈a,b〉=
;(3)cos〈a,b〉=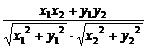 ;
;
(4)a⊥b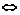 a·b=0
a·b=0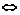 x1x2+y1y2=0.
x1x2+y1y2=0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com