
4.圆锥曲线的几何性质:
(1)椭圆(以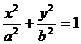 (
(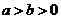 )为例):①范围:
)为例):①范围: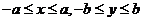 ;②焦点:两个焦点
;②焦点:两个焦点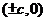 ;③对称性:两条对称轴
;③对称性:两条对称轴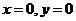 ,一个对称中心(0,0),四个顶点
,一个对称中心(0,0),四个顶点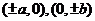 ,其中长轴长为2
,其中长轴长为2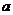 ,短轴长为2
,短轴长为2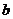 ;④准线:两条准线
;④准线:两条准线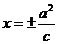 ; ⑤离心率:
; ⑤离心率: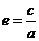 ,椭圆
,椭圆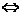
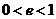 ,
,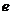 越小,椭圆越圆;
越小,椭圆越圆;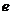 越大,椭圆越扁。如(1)若椭圆
越大,椭圆越扁。如(1)若椭圆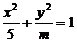 的离心率
的离心率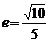 ,则
,则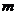 的值是__(答:3或
的值是__(答:3或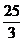 );(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答:
);(2)以椭圆上一点和椭圆两焦点为顶点的三角形的面积最大值为1时,则椭圆长轴的最小值为__(答: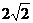 )
)
(2)双曲线(以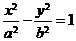 (
(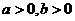 )为例):①范围:
)为例):①范围: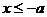 或
或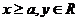 ;②焦点:两个焦点
;②焦点:两个焦点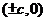 ;③对称性:两条对称轴
;③对称性:两条对称轴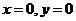 ,一个对称中心(0,0),两个顶点
,一个对称中心(0,0),两个顶点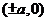 ,其中实轴长为2
,其中实轴长为2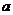 ,虚轴长为2
,虚轴长为2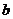 ,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为
,特别地,当实轴和虚轴的长相等时,称为等轴双曲线,其方程可设为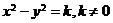 ;④准线:两条准线
;④准线:两条准线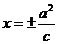 ; ⑤离心率:
; ⑤离心率: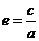 ,双曲线
,双曲线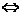
 ,等轴双曲线
,等轴双曲线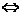
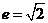 ,
,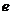 越小,开口越小,
越小,开口越小,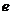 越大,开口越大;⑥两条渐近线:
越大,开口越大;⑥两条渐近线: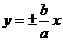 。如(1)双曲线的渐近线方程是
。如(1)双曲线的渐近线方程是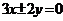 ,则该双曲线的离心率等于______(答:
,则该双曲线的离心率等于______(答: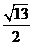 或
或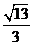 );(2)双曲线
);(2)双曲线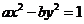 的离心率为
的离心率为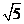 ,则
,则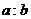 = (答:4或
= (答:4或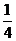 );(3)设双曲线
);(3)设双曲线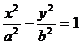 (a>0,b>0)中,离心率e∈[
(a>0,b>0)中,离心率e∈[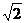 ,2],则两条渐近线夹角θ的取值范围是________(答:
,2],则两条渐近线夹角θ的取值范围是________(答: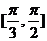 );
);
(3)抛物线(以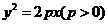 为例):①范围:
为例):①范围: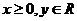 ;②焦点:一个焦点
;②焦点:一个焦点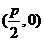 ,其中
,其中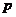 的几何意义是:焦点到准线的距离;③对称性:一条对称轴
的几何意义是:焦点到准线的距离;③对称性:一条对称轴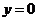 ,没有对称中心,只有一个顶点(0,0);④准线:一条准线
,没有对称中心,只有一个顶点(0,0);④准线:一条准线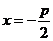 ; ⑤离心率:
; ⑤离心率: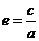 ,抛物线
,抛物线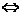
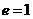 。如设
。如设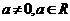 ,则抛物线
,则抛物线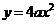 的焦点坐标为________(答:
的焦点坐标为________(答: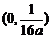 );
);
3.圆锥曲线焦点位置的判断(首先化成标准方程,然后再判断):
(1)椭圆:由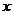
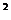 ,
,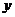
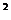 分母的大小决定,焦点在分母大的坐标轴上。如已知方程
分母的大小决定,焦点在分母大的坐标轴上。如已知方程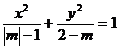 表示焦点在y轴上的椭圆,则m的取值范围是__(答:
表示焦点在y轴上的椭圆,则m的取值范围是__(答: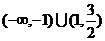 )
)
(2)双曲线:由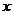
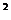 ,
,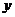
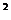 项系数的正负决定,焦点在系数为正的坐标轴上;
项系数的正负决定,焦点在系数为正的坐标轴上;
(3)抛物线:焦点在一次项的坐标轴上,一次项的符号决定开口方向。
特别提醒:(1)在求解椭圆、双曲线问题时,首先要判断焦点位置,焦点F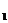 ,F
,F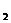 的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数
的位置,是椭圆、双曲线的定位条件,它决定椭圆、双曲线标准方程的类型,而方程中的两个参数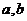 ,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,
,确定椭圆、双曲线的形状和大小,是椭圆、双曲线的定形条件;在求解抛物线问题时,首先要判断开口方向;(2)在椭圆中,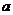 最大,
最大,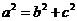 ,在双曲线中,
,在双曲线中,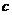 最大,
最大,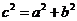 。
。
2.圆锥曲线的标准方程(标准方程是指中心(顶点)在原点,坐标轴为对称轴时的标准位置的方程):
(1)椭圆:焦点在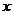 轴上时
轴上时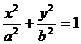 (
(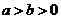 )
)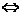
 (参数方程,其中
(参数方程,其中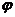 为参数),焦点在
为参数),焦点在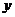 轴上时
轴上时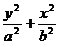 =1(
=1(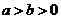 )。方程
)。方程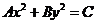 表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。如(1)已知方程
表示椭圆的充要条件是什么?(ABC≠0,且A,B,C同号,A≠B)。如(1)已知方程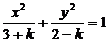 表示椭圆,则
表示椭圆,则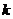 的取值范围为____(答:
的取值范围为____(答: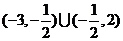 );(2)若
);(2)若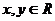 ,且
,且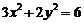 ,则
,则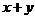 的最大值是____,
的最大值是____,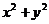 的最小值是___(答:
的最小值是___(答: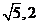 )
)
(2)双曲线:焦点在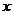 轴上:
轴上: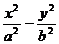 =1,焦点在
=1,焦点在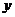 轴上:
轴上: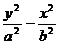 =1(
=1(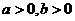 )。方程
)。方程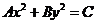 表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。如(1)双曲线的离心率等于
表示双曲线的充要条件是什么?(ABC≠0,且A,B异号)。如(1)双曲线的离心率等于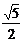 ,且与椭圆
,且与椭圆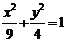 有公共焦点,则该双曲线的方程_______(答:
有公共焦点,则该双曲线的方程_______(答: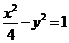 );(2)设中心在坐标原点
);(2)设中心在坐标原点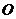 ,焦点
,焦点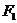 、
、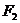 在坐标轴上,离心率
在坐标轴上,离心率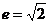 的双曲线C过点
的双曲线C过点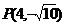 ,则C的方程为_______(答:
,则C的方程为_______(答: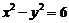 )
)
(3)抛物线:开口向右时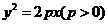 ,开口向左时
,开口向左时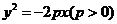 ,开口向上时
,开口向上时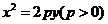 ,开口向下时
,开口向下时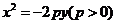 。
。
1.圆锥曲线的两个定义:
(1)第一定义中要重视“括号”内的限制条件:椭圆中,与两个定点F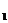 ,F
,F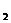 的距离的和等于常数
的距离的和等于常数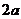 ,且此常数
,且此常数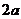 一定要大于
一定要大于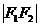 ,当常数等于
,当常数等于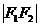 时,轨迹是线段F
时,轨迹是线段F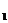 F
F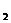 ,当常数小于
,当常数小于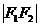 时,无轨迹;双曲线中,与两定点F
时,无轨迹;双曲线中,与两定点F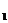 ,F
,F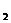 的距离的差的绝对值等于常数
的距离的差的绝对值等于常数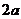 ,且此常数
,且此常数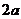 一定要小于|F
一定要小于|F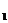 F
F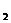 |,定义中的“绝对值”与
|,定义中的“绝对值”与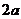 <|F
<|F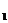 F
F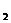 |不可忽视。若
|不可忽视。若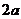 =|F
=|F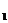 F
F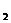 |,则轨迹是以F
|,则轨迹是以F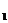 ,F
,F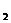 为端点的两条射线,若
为端点的两条射线,若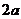 ﹥|F
﹥|F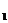 F
F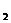 |,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。如(1)已知定点
|,则轨迹不存在。若去掉定义中的绝对值则轨迹仅表示双曲线的一支。如(1)已知定点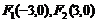 ,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.
,在满足下列条件的平面上动点P的轨迹中是椭圆的是 A.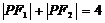 B.
B.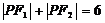 C.
C.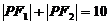 D.
D.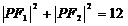 (答:C);(2)方程
(答:C);(2)方程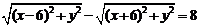 表示的曲线是_____(答:双曲线的左支)
表示的曲线是_____(答:双曲线的左支)
(2)第二定义中要注意定点和定直线是相应的焦点和准线,且“点点距为分子、点线距为分母”,其商即是离心率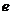 。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。如已知点
。圆锥曲线的第二定义,给出了圆锥曲线上的点到焦点距离与此点到相应准线距离间的关系,要善于运用第二定义对它们进行相互转化。如已知点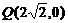 及抛物线
及抛物线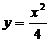 上一动点P(x,y),则y+|PQ|的最小值是_____(答:2)
上一动点P(x,y),则y+|PQ|的最小值是_____(答:2)
12、向量中一些常用的结论:
(1)一个封闭图形首尾连接而成的向量和为零向量,要注意运用;
(2)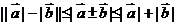 ,特别地,当
,特别地,当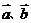 同向或有
同向或有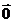
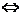
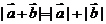
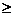
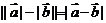 ;当
;当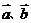 反向或有
反向或有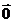
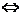
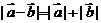
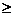
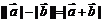 ;当
;当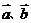 不共线
不共线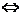
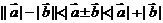 (这些和实数比较类似).
(这些和实数比较类似).
(3)在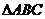 中,①若
中,①若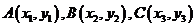 ,则其重心的坐标为
,则其重心的坐标为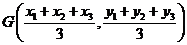 。如若⊿ABC的三边的中点分别为(2,1)、(-3,4)、 (-1,-1),则⊿ABC的重心的坐标为_______(答:
。如若⊿ABC的三边的中点分别为(2,1)、(-3,4)、 (-1,-1),则⊿ABC的重心的坐标为_______(答: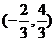 );
);
②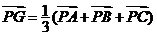
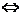
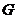 为
为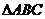 的重心,特别地
的重心,特别地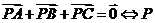 为
为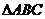 的重心;
的重心;
③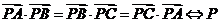 为
为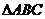 的垂心;
的垂心;
④向量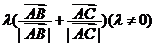 所在直线过
所在直线过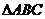 的内心(是
的内心(是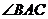 的角平分线所在直线);
的角平分线所在直线);
⑤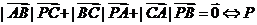
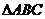 的内心;
的内心;
(3)若P分有向线段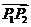 所成的比为
所成的比为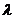 ,点
,点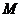 为平面内的任一点,则
为平面内的任一点,则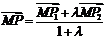 ,特别地
,特别地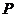 为
为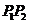 的中点
的中点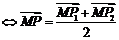 ;
;
(4)向量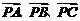 中三终点
中三终点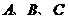 共线
共线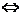 存在实数
存在实数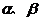 使得
使得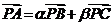 且
且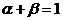 .如平面直角坐标系中,
.如平面直角坐标系中,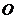 为坐标原点,已知两点
为坐标原点,已知两点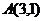 ,
,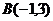 ,若点
,若点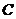 满足
满足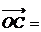
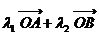 ,其中
,其中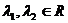 且
且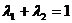 ,则点
,则点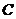 的轨迹是_______(答:直线AB)
的轨迹是_______(答:直线AB)
11.平移公式:如果点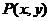 按向量
按向量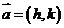 平移至
平移至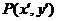 ,则
,则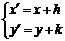 ;曲线
;曲线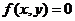 按向量
按向量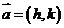 平移得曲线
平移得曲线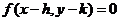 .注意:(1)函数按向量平移与平常“左加右减”有何联系?(2)向量平移具有坐标不变性,可别忘了啊!如(1)按向量
.注意:(1)函数按向量平移与平常“左加右减”有何联系?(2)向量平移具有坐标不变性,可别忘了啊!如(1)按向量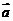 把
把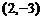 平移到
平移到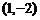 ,则按向量
,则按向量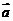 把点
把点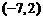 平移到点______(答:(-8,3));(2)函数
平移到点______(答:(-8,3));(2)函数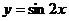 的图象按向量
的图象按向量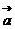 平移后,所得函数的解析式是
平移后,所得函数的解析式是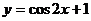 ,则
,则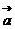 =________(答:
=________(答: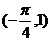 )
)
10.线段的定比分点:
(1)定比分点的概念:设点P是直线P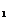 P
P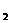 上异于P
上异于P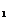 、P
、P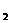 的任意一点,若存在一个实数
的任意一点,若存在一个实数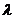 ,使
,使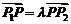 ,则
,则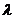 叫做点P分有向线段
叫做点P分有向线段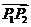 所成的比,P点叫做有向线段
所成的比,P点叫做有向线段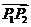 的以定比为
的以定比为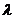 的定比分点;
的定比分点;
(2)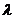 的符号与分点P的位置之间的关系:当P点在线段 P
的符号与分点P的位置之间的关系:当P点在线段 P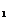 P
P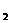 上时
上时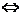
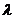 >0;当P点在线段
P
>0;当P点在线段
P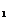 P
P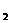 的延长线上时
的延长线上时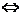
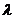 <-1;当P点在线段P
<-1;当P点在线段P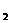 P
P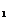 的延长线上时
的延长线上时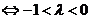 ;若点P分有向线段
;若点P分有向线段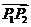 所成的比为
所成的比为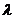 ,则点P分有向线段
,则点P分有向线段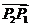 所成的比为
所成的比为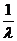 。如若点
。如若点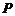 分
分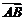 所成的比为
所成的比为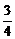 ,则
,则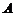 分
分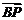 所成的比为_______(答:
所成的比为_______(答: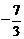 )
)
(3)线段的定比分点公式:设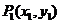 、
、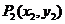 ,
,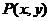 分有向线段
分有向线段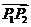 所成的比为
所成的比为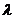 ,则
,则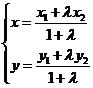 ,特别地,当
,特别地,当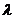 =1时,就得到线段P
=1时,就得到线段P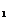 P
P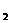 的中点公式
的中点公式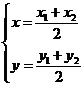 。在使用定比分点的坐标公式时,应明确
。在使用定比分点的坐标公式时,应明确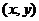 ,
,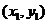 、
、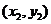 的意义,即分别为分点,起点,终点的坐标。在具体计算时应根据题设条件,灵活地确定起点,分点和终点,并根据这些点确定对应的定比
的意义,即分别为分点,起点,终点的坐标。在具体计算时应根据题设条件,灵活地确定起点,分点和终点,并根据这些点确定对应的定比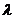 。如(1)若M(-3,-2),N(6,-1),且
。如(1)若M(-3,-2),N(6,-1),且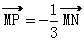 ,则点P的坐标为_______(答:
,则点P的坐标为_______(答: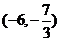 );(2)已知
);(2)已知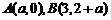 ,直线
,直线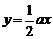 与线段
与线段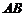 交于
交于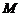 ,且
,且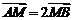 ,则
,则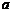 等于_______(答:2或-4)
等于_______(答:2或-4)
9、向量垂直的充要条件: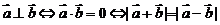
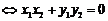 .特别地
.特别地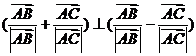 。如(1)已知
。如(1)已知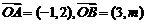 ,若
,若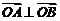 ,则
,则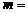 (答:
(答: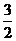 );(2)以原点O和A(4,2)为两个顶点作等腰直角三角形OAB,
);(2)以原点O和A(4,2)为两个顶点作等腰直角三角形OAB,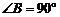 ,则点B的坐标是________ (答:(1,3)或(3,-1));(3)已知
,则点B的坐标是________ (答:(1,3)或(3,-1));(3)已知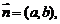 向量
向量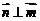 ,且
,且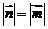 ,则
,则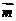 的坐标是________ (答:
的坐标是________ (答: )
)
8、向量平行(共线)的充要条件: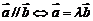
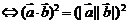
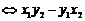 =0。如(1)若向量
=0。如(1)若向量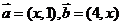 ,当
,当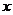 =_____时
=_____时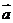 与
与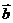 共线且方向相同(答:2);(2)已知
共线且方向相同(答:2);(2)已知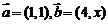 ,
,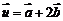 ,
,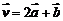 ,且
,且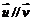 ,则x=______(答:4);(3)设
,则x=______(答:4);(3)设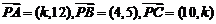 ,则k=_____时,A,B,C共线(答:-2或11)
,则k=_____时,A,B,C共线(答:-2或11)
7、向量的运算律:(1)交换律: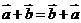 ,
,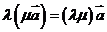 ,
,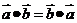 ;(2)结合律:
;(2)结合律: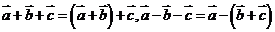 ,
,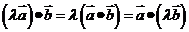 ;(3)分配律:
;(3)分配律: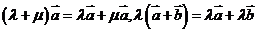 ,
,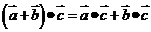 。如下列命题中:①
。如下列命题中:① 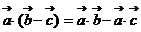 ;②
;② 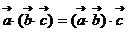 ;③
;③ 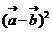
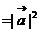
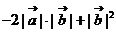 ;④ 若
;④ 若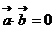 ,则
,则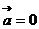 或
或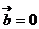 ;⑤若
;⑤若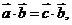 则
则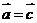 ;⑥
;⑥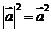 ;⑦
;⑦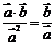 ;⑧
;⑧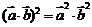 ;⑨
;⑨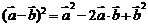 。其中正确的是______(答:①⑥⑨)
。其中正确的是______(答:①⑥⑨)
提醒:(1)向量运算和实数运算有类似的地方也有区别:对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边同乘以一个向量,但不能两边同除以一个向量,即两边不能约去一个向量,切记两向量不能相除(相约);(2)向量的“乘法”不满足结合律,即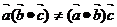 ,为什么?
,为什么?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com