
28.(08山东滨州)24.(本题满分12分)
如图(1),已知在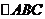 中,AB=AC=10,AD为底边BC上的高,且AD=6。将
中,AB=AC=10,AD为底边BC上的高,且AD=6。将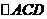 沿箭头所示的方向平移,得到
沿箭头所示的方向平移,得到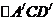 。如图(2),
。如图(2),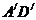 交AB于E,
交AB于E,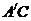 分别交AB、AD于G、F。以
分别交AB、AD于G、F。以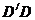 为直径作
为直径作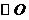 ,设
,设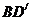 的长为x,
的长为x,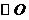 的面积为y。
的面积为y。
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连结EF,求EF与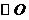 相切时x的值;
相切时x的值;
(3)设四边形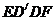 的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
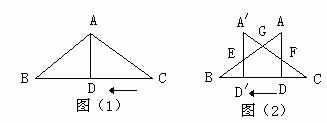
(08山东滨州24题解析)24.
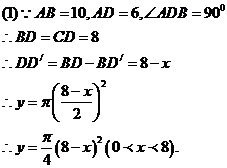
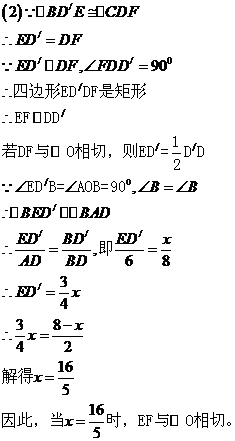
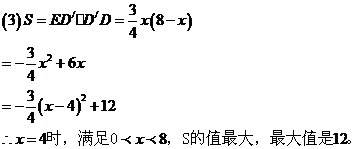
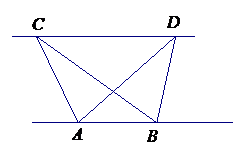
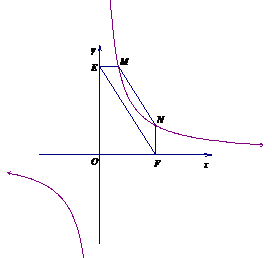
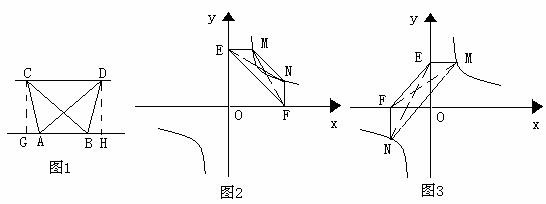
27.(08山东滨州)23、(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:①如图2,点M、N在反比例函数y=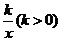 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试应用(1)中得到的结论证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试应用(1)中得到的结论证明:MN∥EF.
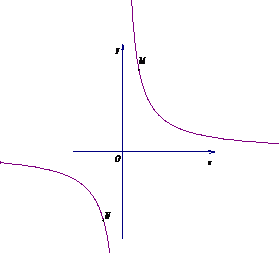
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与E是否平行.
(08山东滨州23题解析)23.(1)证明:分别过点C、D作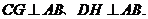
垂足为G、H,则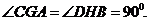
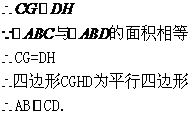
(2)①证明:连结MF,NE
设点M的坐标为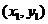 ,点N的坐标为
,点N的坐标为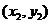 ,
,
∵点M,N在反比例函数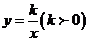 的图象上,
的图象上,
∴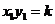 ,
,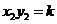
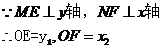
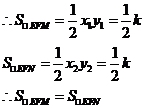
由(1)中的结论可知:MN∥EF。
②MN∥EF。
3.第(4)问图形画得大致正确的得2分,只画出图形一部分的得1分.
2.第(3)问表格数据,每填对其中4空得1分;
26.(08江西南昌)25.如图1,正方形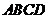 和正三角形
和正三角形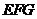 的边长都为1,点
的边长都为1,点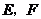 分别在线段
分别在线段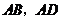 上滑动,设点
上滑动,设点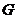 到
到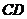 的距离为
的距离为 ,到
,到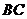 的距离为
的距离为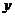 ,记
,记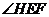 为
为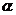 (当点
(当点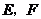 分别与
分别与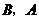 重合时,记
重合时,记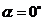 ).
).
(1)当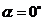 时(如图2所示),求
时(如图2所示),求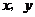 的值(结果保留根号);
的值(结果保留根号);
(2)当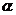 为何值时,点
为何值时,点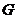 落在对角形
落在对角形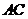 上?请说出你的理由,并求出此时
上?请说出你的理由,并求出此时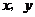 的值(结果保留根号);
的值(结果保留根号);
(3)请你补充完成下表(精确到0.01):
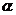 |
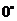 |
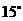 |
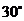 |
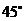 |
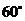 |
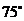 |
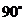 |
 |
|
0.03 |
0 |
|
|
0.29 |
|
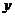 |
|
0.29 |
0.13 |
|
|
0.03 |
|
(4)若将“点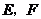 分别在线段
分别在线段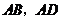 上滑动”改为“点
上滑动”改为“点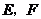 分别在正方形
分别在正方形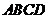 边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点
边上滑动”.当滑动一周时,请使用(3)的结果,在图4中描出部分点后,勾画出点 运动所形成的大致图形.
运动所形成的大致图形.
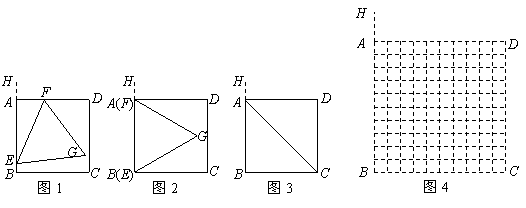 (参考数据:
(参考数据: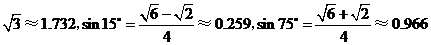 .)
.)
(08江西南昌25题解析)25.解:(1)过 作
作 于
于 交
交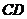 于
于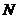 ,
,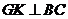 于
于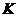 .
.
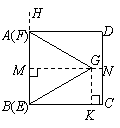
 ,
, ,
,
 ,
,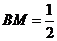 .······················································································ 2分
.······················································································ 2分
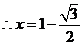 ,
,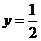 .························································································· 3分
.························································································· 3分
(2)当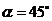 时,点
时,点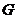 在对角线
在对角线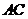 上,其理由是:·········································· 4分
上,其理由是:·········································· 4分
过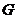 作
作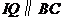 交
交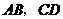 于
于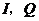 ,
,
过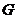 作
作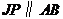 交
交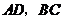 于
于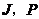 .
.
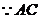 平分
平分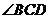 ,
,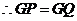 ,
,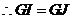 .
.
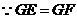 ,
,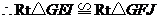 ,
,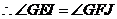 .
.
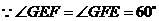 ,
,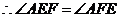 .
.
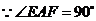 ,
,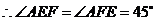 .
.
 即
即 时,点
时,点 落在对角线
落在对角线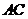 上.································································ 6分
上.································································ 6分
(以下给出两种求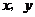 的解法)
的解法)
方法一: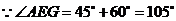 ,
,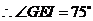 .
.
在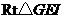 中,
中,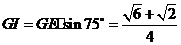 ,
,
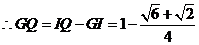 .·········································································· 7分
.·········································································· 7分
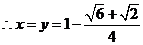 .························································································ 8分
.························································································ 8分
方法二:当点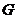 在对角线
在对角线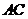 上时,有
上时,有
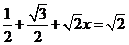 ,··························································································· 7分
,··························································································· 7分
解得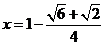
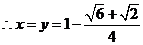 .························································································ 8分
.························································································ 8分
(3)
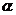 |
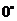 |
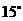 |
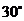 |
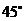 |
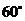 |
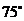 |
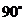 |
 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
0.29 |
0.50 |
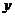 |
0.50 |
0.29 |
0.13 |
0.03 |
0 |
0.03 |
0.13 |
································································ 10分
(4)由点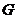 所得到的大致图形如图所示:
所得到的大致图形如图所示:

 ··························································································· 12分
··························································································· 12分
说明:1.第(2)问回答正确的得1分,证明正确的得2分,求出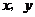 的值各得1分;
的值各得1分;
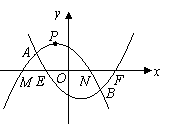
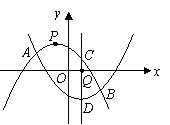
25.(08江西南昌)24.如图,抛物线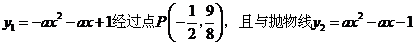 相交于
相交于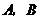 两点.
两点.
(1)求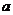 值;
值;
(2)设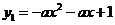 与
与 轴分别交于
轴分别交于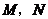 两点(点
两点(点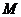 在点
在点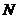 的左边),
的左边),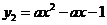 与
与 轴分别交于
轴分别交于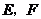 两点(点
两点(点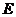 在点
在点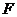 的左边),观察
的左边),观察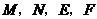 四点的坐标,写出一条正确的结论,并通过计算说明;
四点的坐标,写出一条正确的结论,并通过计算说明;
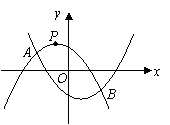 (3)设
(3)设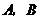 两点的横坐标分别记为
两点的横坐标分别记为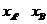 ,若在
,若在 轴上有一动点
轴上有一动点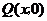 ,且
,且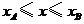 ,过
,过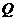 作一条垂直于
作一条垂直于 轴的直线,与两条抛物线分别交于C,D两点,试问当
轴的直线,与两条抛物线分别交于C,D两点,试问当 为何值时,线段CD有最大值?其最大值为多少?
为何值时,线段CD有最大值?其最大值为多少?
(08江西南昌24题解析)24.解:(1) 点
点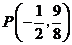 在抛物线
在抛物线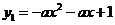 上,
上,
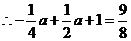 ,··························································································· 2分
,··························································································· 2分
解得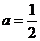 .··········································································································· 3分
.··········································································································· 3分
(2)由(1)知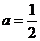 ,
,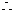 抛物线
抛物线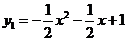 ,
,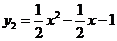 .······· 5分
.······· 5分
 当
当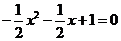 时,解得
时,解得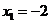 ,
,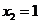 .
.
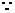 点
点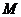 在点
在点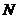 的左边,
的左边,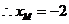 ,
,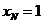 .············ 6分
.············ 6分
当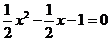 时,解得
时,解得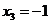 ,
,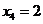 .
.
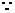 点
点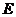 在点
在点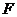 的左边,
的左边,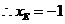 ,
,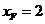 .························································ 7分
.························································ 7分
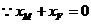 ,
,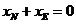 ,
,
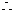 点
点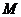 与点
与点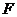 对称,点
对称,点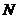 与点
与点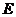 对称.(8分)
对称.(8分)
(3)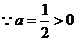 .
.
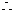 抛物线
抛物线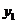 开口向下,抛物线
开口向下,抛物线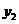 开口向上.················ 9分
开口向上.················ 9分
根据题意,得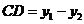
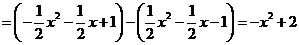 .··············································· 11分
.··············································· 11分
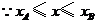 ,
,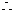 当
当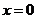 时,
时,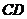 有最大值
有最大值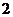 .··············································· 12分
.··············································· 12分
说明:第(2)问中,结论写成“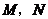 ,
,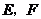 四点横坐标的代数和为0”或“
四点横坐标的代数和为0”或“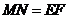 ”均得1分.
”均得1分.
4.从弱引力到强引力
疑点
只要天体的实际半径远大于它们的引力半径,那么由爱因斯坦引力理论和牛顿引力理论计算出的力的差异并不是很大。但当天体的实际半径接近引力半径时,这种差异将急剧增大。这就是说,在强引力的情况下,牛顿的引力理论将不再适用。
易错点
经典力学的适用范围:低速、宏观物体的运动。
量子力学的研究对象:高速、微观物体的运动。
教学资源
重要的思想方法
通过对牛顿、爱因斯坦等于科学家关于经典力学与量子力学理论的介绍,领略到前辈科学家们对自然奥秘不屈不挠探索的精神和对待科学研究一丝不苟的态度,感悟到科学的结论总是在顽强曲折的科学实践中悄悄地来临。
3.从宏观到微观
2.从低速到高速
1.经典力学的成就与局限性
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com