
5.(2005年辽宁卷)如图所示,已知 为坐标原点,
为坐标原点,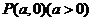 为
为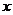 轴上一动点,过点
轴上一动点,过点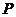 作直线交抛物线
作直线交抛物线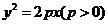 于
于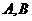 两点,
两点,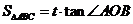 ,试问:当
,试问:当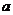 为何值时,
为何值时,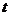 取得最小值,并求出这个最小值。
取得最小值,并求出这个最小值。
例6.给定双曲线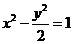 .
.
(1)过点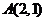 的直线
的直线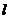 与所给的双曲线交于
与所给的双曲线交于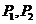 ,求线段
,求线段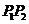 的中点
的中点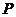 的轨迹方程;
的轨迹方程;
(2)过点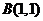 能否作直线
能否作直线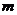 ,使
,使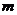 与所给的双曲线交于
与所给的双曲线交于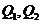 ,且
,且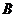 是线段
是线段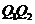 的中点?若存在,求出直线方程.如果不存在,请说明理由。
的中点?若存在,求出直线方程.如果不存在,请说明理由。
[剖析]本题是探索性问题,考查方程思想,韦达定理及解析几何中的“设而不求”的思想。
[解](1)解法一:设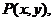
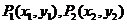 ,
,
(i)若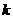 存在,则由
存在,则由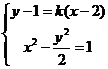 可得
可得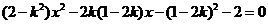 ,
,
|
|
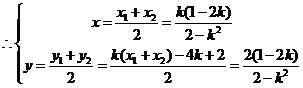
①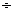 ②,得
②,得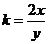 ,代入②,得
,代入②,得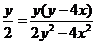
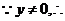 有
有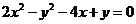
(ii)当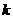 不存在时,有
不存在时,有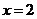 ,则
,则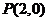 也合符合上式。
也合符合上式。
综合(i)(ii)可知点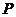 的轨迹方程为
的轨迹方程为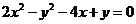 .
.
解法二:设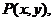
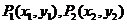 ,则
,则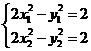 ,
,
两式相减,得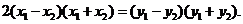
当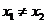 ,
,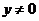 时,
时,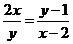 ,即
,即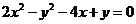 ;
;
当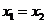 时,
时,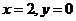 也满足
也满足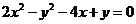 .
.
故点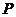 的轨迹方程为
的轨迹方程为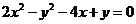 .
.
(2)假设满足题设条件的直线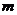 存在,设
存在,设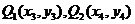
可得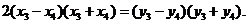
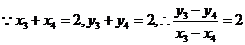 ,
,
直线的方程为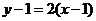 ,即
,即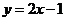
由于方程组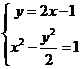 无解,故满足条件的直线
无解,故满足条件的直线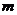 不存在。
不存在。
[警示]探索性试题常见的题型有两类:一类是给出问题对象的一些特殊关系,要求解题者探索出一般规律,并能论证所得规律的正确性;通常要求对已知关系进行观察、比较、分析,然后概括出一般规律。第二类是只给出条件,要求解题者论证在此条件下,会不会出现某个结论,这类问题常以适合某种条件下的结论“存在”、“不存在”与“是否存在”等词语表述.解决这类问题,一般要先对结论作出肯定存在的假设,然后由假设出发,结合已知条件进行推理论证,若推出相符的结论,则存在性也随之解决;若推导出矛盾,则否定了存在性。
[变式训练]
4.直线l经过点(1,1),若抛物线y2=x上存在两点关于直线l对称,求直线l斜率的取值范围.
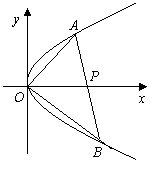
例5.设椭圆方程为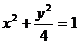 ,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足
,过点M(0,1)的直线l交椭圆于点A、B,O是坐标原点,点P满足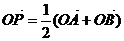 ,点N的坐标为
,点N的坐标为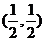 ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)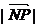 的最小值与最大值.
的最小值与最大值.
[剖析]本题分成了两个小问题,第一个小问题是求轨迹问题,可借助于求轨迹的方法处理;对于第二小问,结合题目的特点可以借助函数的单调性来加以解决。
[解](1)解法一:直线l过点M(0,1)设其斜率为k,则l的方程为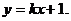
记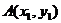 、
、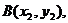 由题设可得点A、B的坐标
由题设可得点A、B的坐标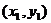 、
、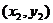 是方程组
是方程组
|
|
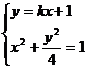 的解. 将①代入②并化简得,
的解. 将①代入②并化简得,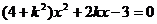 ,所以
,所以
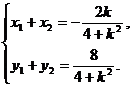 于是
于是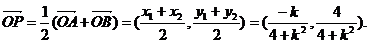
设点P的坐标为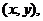 则
则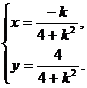 消去参数k得
消去参数k得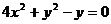 ③
③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以点P的轨迹方
程为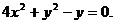
解法二:设点P的坐标为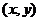 ,因
,因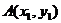 、
、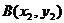 在椭圆上,所以
在椭圆上,所以
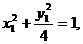 ④
④ 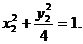 ⑤
⑤
④-⑤得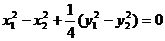 ,所以
,所以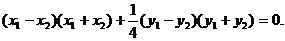
当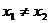 时,有
时,有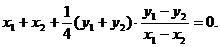 ⑥
⑥
并且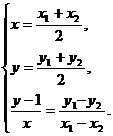 ⑦ 将⑦代入⑥并整理得
⑦ 将⑦代入⑥并整理得
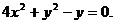 ⑧
⑧
当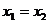 时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)
时,点A、B的坐标为(0,2)、(0,-2),这时点P的坐标为(0,0)
也满足⑧,所以点P的轨迹方程为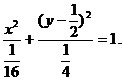
(2)解:由点P的轨迹方程知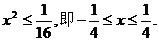 所以
所以
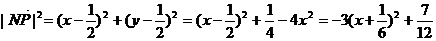
故当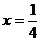 ,
,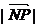 取得最小值,最小值为
取得最小值,最小值为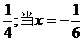 时,
时,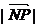 取得最大值,
取得最大值,
最大值为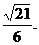
 [警示]本题主要考查圆锥曲线的最值问题,此类问题的求解策略主要有两种:(1)几何法:若题目条件和结论能明显体现某一曲线的几何特征及意义,则可以考虑结合图形来加以解决;(2)代数法:若题目的条件和结论能体现一种明确的函数,则可以首先建立起目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法及函数的单调性法等。
[警示]本题主要考查圆锥曲线的最值问题,此类问题的求解策略主要有两种:(1)几何法:若题目条件和结论能明显体现某一曲线的几何特征及意义,则可以考虑结合图形来加以解决;(2)代数法:若题目的条件和结论能体现一种明确的函数,则可以首先建立起目标函数,再求这个函数的最值,求函数的最值常用的方法有配方法、判别式法及函数的单调性法等。
[变式训练]
3.对于每个正整数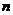 ,
,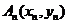 是抛物线
是抛物线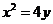 上的点,过焦点
上的点,过焦点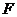 的直线
的直线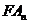 交抛物线于另一点
交抛物线于另一点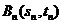
(1)求证: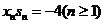 ;
;
(2)取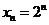 ,并记
,并记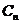 为抛物线上分别以
为抛物线上分别以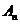 与
与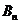 为切点的两条切线的交点.
为切点的两条切线的交点.
试证: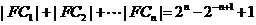 .
.
例4.已知椭圆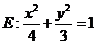 ,试确定
,试确定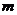 的取值范围,便得椭圆
的取值范围,便得椭圆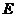 上存在不同的两点关于直线
上存在不同的两点关于直线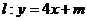 对称。
对称。
[剖析]直接设出这两个不同点的坐标,由点的坐标适合椭圆方程、经过这两点的直线斜率的表示、这两点的中点在椭圆内几个已知条件,列出关系式,联立求解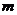 范围;也可以把这两个不同的点所确定直线的方程设出来与椭圆方程联立,运用一元二次方程判断式及韦达定理分析求解。
范围;也可以把这两个不同的点所确定直线的方程设出来与椭圆方程联立,运用一元二次方程判断式及韦达定理分析求解。
|
|
|
|
|
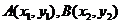 是椭圆
是椭圆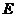 上关于直线
上关于直线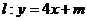 的两个对称点,则
的两个对称点,则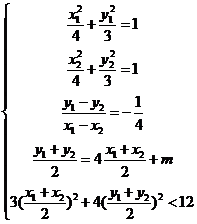
|
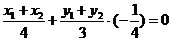 ,
,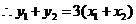
联立④⑥得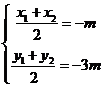 代入⑤,得
代入⑤,得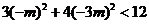
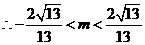 .
.
解法二:把对称点视为直线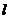 垂直平分弦之两端.设
垂直平分弦之两端.设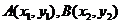 是椭圆
是椭圆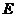 上关于
上关于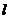 对称的两点,则
对称的两点,则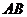 所在的直线方程为
所在的直线方程为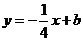 与椭圆方程
与椭圆方程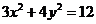 联立,消去
联立,消去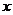 得
得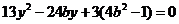 .
.
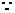 此方程有二个实根,
此方程有二个实根,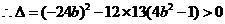 ,解之得:
,解之得: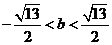 (*)
(*)
由韦达定理,得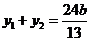 ,
,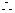 弦
弦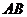 中点纵坐标是
中点纵坐标是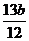 .
.
又弦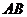 中点是直线
中点是直线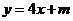 与
与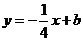 的公共点,
的公共点,
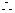 解方程组
解方程组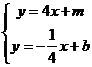 ,得弦
,得弦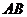 中点为
中点为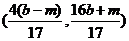 ,
,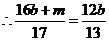 ,即
,即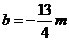 ,代入(*)式,得
,代入(*)式,得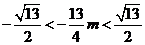 ,即
,即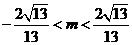 .
.
[警示]本题把点和直线放在椭圆中考查,又运用了椭圆的有关几何性质,常见有两种思考方法:一是由条件联立方程组整体分析和代换求解;二是应用一元二次方程的判别式及韦达定理,进行分析求解.对于圆锥曲线上存在两点关于某一条直线对称,求有关参数的问题,可以用参数表示弦的中点的坐标,利用中点在曲线的内部和在直线上等条件,建立不等式或不等式组来求出参数的范围;或者利用对称条件求出过这两点的直线方程,利用判断式大于零,建立不等式进行求解。
[变式训练]
1.
椭圆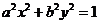 与直线
与直线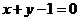 相交于
相交于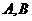 两点,
两点,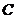 是
是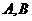 的中点.若
的中点.若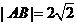 ,直线
,直线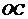 的斜率为
的斜率为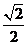 ,求椭圆的方程。
,求椭圆的方程。
例3.过点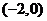 的直线
的直线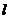 与抛物线
与抛物线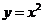 相交于
相交于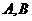 两点,求
两点,求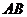 中点的轨迹方程。
中点的轨迹方程。
[剖析]求中点的轨迹方程,可以借助于点差法与韦达定理来解决。
[解]易知直线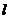 的斜率一定存在,设直线
的斜率一定存在,设直线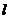 的方程为
的方程为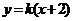 ,再设
,再设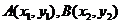 ,
,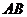 的中点坐标为
的中点坐标为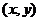 ,则
,则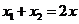 ,则
,则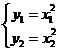
两式作差,得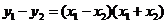 ,那么
,那么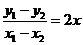 ,由于
,由于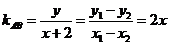 ,得
,得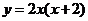 ,即
,即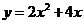 .
.
又由于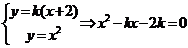 ,由
,由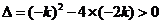 ,得
,得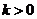 或
或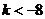 ,
,
由于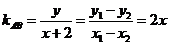 ,可得
,可得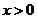 或
或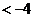
从而所得轨迹方程为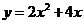 (
(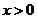 或
或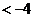 ).
).
[警示]整体运算,本题可以作为一典型题目,它通过整体推理、整体代换等有效地绕过许多中间环节使运算直指结论。它既可优化解题过程又可以给我们带来一种赏心悦目的解题享受.本题借助于整体运算产生中点的轨迹方程,其过程简练、运算简单. 在欣赏整体运算的同时,需要注意解析的后部分,借助方程组产生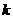 的范围,这是多同学容易漏掉的地方,少了它,结论的完备性就不存在了。
的范围,这是多同学容易漏掉的地方,少了它,结论的完备性就不存在了。
[变式训练]
1.对于抛物线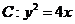 ,称满足
,称满足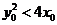 的点有抛物线的内部.若点
的点有抛物线的内部.若点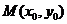 在抛物线
在抛物线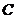 的内部,试求直线
的内部,试求直线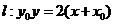 与抛物线
与抛物线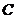 的公共点的个数.
的公共点的个数.
例2.过点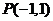 作直线与椭圆
作直线与椭圆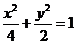 交于
交于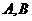 两点,若线段
两点,若线段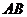 的中点为
的中点为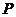 ,求直线
,求直线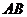 所在的直线方程和线段
所在的直线方程和线段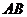 的长度.
的长度.
[剖析]由点差法可容易求解出直线方程,知道直线方程,借助弦长公式可求出线段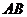 的长度。本题采用了设而不求的方法,即设点,代入,作差,借助于直线的斜率解题方法,这种方法称为“点差法”,是解析几何解决直线与圆锥曲线问题的常用的技巧之一,应在理解的基础上进行训练.
的长度。本题采用了设而不求的方法,即设点,代入,作差,借助于直线的斜率解题方法,这种方法称为“点差法”,是解析几何解决直线与圆锥曲线问题的常用的技巧之一,应在理解的基础上进行训练.
[解]设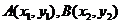 ,由
,由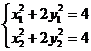 得
得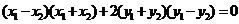 ,显然
,显然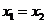 不合题意,
不合题意,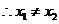 ,
,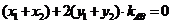 ,
,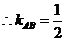 ,从而直线
,从而直线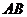 的方程为
的方程为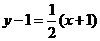 ,即
,即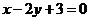 .
.
由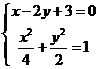 ,得
,得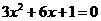 ,
,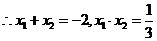
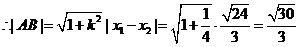 .
.
[警示]本题还可以设出直线的方程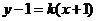 代入椭圆方程,运用韦达定理,求出直线的斜率.直线与椭圆相交,出现中点弦问题的常规处理方法有三种:(1)通过方程组转化为一元二次方程,结合韦达定理及中点坐标公式进行求解;(2)点差法,设出两端点的坐标,利用中点坐标公式求解;(3)中点转移法,先设出一个端点的坐标,再借助中点设出另一个端点的坐标,而后消去二次项.
代入椭圆方程,运用韦达定理,求出直线的斜率.直线与椭圆相交,出现中点弦问题的常规处理方法有三种:(1)通过方程组转化为一元二次方程,结合韦达定理及中点坐标公式进行求解;(2)点差法,设出两端点的坐标,利用中点坐标公式求解;(3)中点转移法,先设出一个端点的坐标,再借助中点设出另一个端点的坐标,而后消去二次项.
[变式训练]
6.已知直线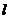 与抛物线
与抛物线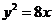 交于
交于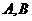 两点,且
两点,且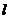 过抛物线的焦点
过抛物线的焦点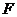 ,点A的坐标为
,点A的坐标为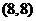 ,则线段AB的中点到抛物线准线的距离是
.
,则线段AB的中点到抛物线准线的距离是
.
[典例精析]
例1.已知直线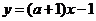 与曲线
与曲线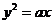 恰有一个公共点,求实数
恰有一个公共点,求实数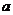 的值。
的值。
[剖析]首先考虑曲线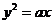 是否是抛物线,当
是否是抛物线,当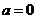 时,是直线
时,是直线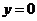 ,因此要对
,因此要对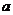 进行讨论,然后就
进行讨论,然后就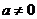 时,联立直线与抛物线组成的方程组进行求解。
时,联立直线与抛物线组成的方程组进行求解。
[解]联立方程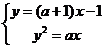
(1)当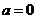 时,此方程组恰有组解
时,此方程组恰有组解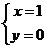 ;
;
(2)当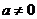 时,消去
时,消去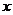 ,得
,得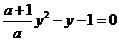 ;
;
①当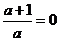 ,即
,即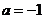 时,方程变为一元一次方程
时,方程变为一元一次方程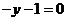 ,方程恰有一组解
,方程恰有一组解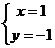 ;
;
②若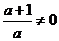 ,即
,即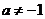 时,令
时,令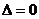 ,得
,得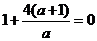 ,解得
,解得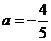 ,此时直线与曲线相切,有且只有一个公共点.
,此时直线与曲线相切,有且只有一个公共点.
综上所述,当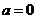 ,
,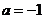 或
或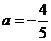 时,直线与曲线
时,直线与曲线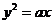 恰有一个公共点。
恰有一个公共点。
[警示]本题设计了两个思维陷阱,第一个就是同学们在审请的过程中往往视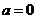 的情况,误认为
的情况,误认为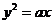 对应的曲线就是抛物线;第二个是在解答的过程中不讨论二次项系数
对应的曲线就是抛物线;第二个是在解答的过程中不讨论二次项系数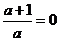 即
即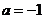 的可能,从而漏掉两个解.另外,在研究直线与圆锥曲线的位置关系时,应特别注意
的可能,从而漏掉两个解.另外,在研究直线与圆锥曲线的位置关系时,应特别注意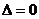 并不是直线与曲线有且只有一个公共点的充要条件.事实上,求曲线与曲线的点的个数,就是它们的方程组成的方程组解的个数。在具体解方程时,需要比较消去
并不是直线与曲线有且只有一个公共点的充要条件.事实上,求曲线与曲线的点的个数,就是它们的方程组成的方程组解的个数。在具体解方程时,需要比较消去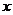 与消去
与消去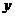 哪个简单,从而选择恰当的消参方式,还要注意
哪个简单,从而选择恰当的消参方式,还要注意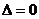 只是是直线与曲线有且只有一个公共点的充分不必要条件.
只是是直线与曲线有且只有一个公共点的充分不必要条件.
[变式训练]:
5.过抛物线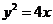 的焦点
的焦点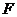 作垂直与
作垂直与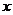 轴的直线,交抛物线于
轴的直线,交抛物线于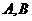 两点,则以
两点,则以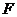 为圆心,
为圆心,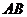 为直径的圆的方程是
.
为直径的圆的方程是
.
4.(2005年济南模拟试题)直线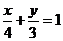 与椭圆
与椭圆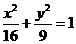 相交于
相交于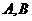 两点,椭圆上的点
两点,椭圆上的点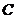 使
使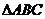 的面积等于12,这样的点C共有( )
的面积等于12,这样的点C共有( )
(A)1个 (B)2个 (C)3个 (D)4个
3.抛物线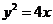 过焦点的弦的中点的轨迹方程是( )
过焦点的弦的中点的轨迹方程是( )
(A) 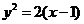 (B)
(B) 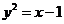 (C)
(C) 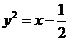 (D)
(D) 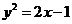
2.与直线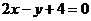 平行的抛物线
平行的抛物线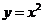 的切线方程为( )
的切线方程为( )
(A)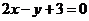 (B)
(B) 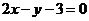 (C)
(C) 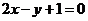 (D)
(D) 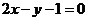
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com