
2.(2008年江西五校联考)已知正整数a,b满足4a+b=30,使得+取最小值时,则实数对(a,b)是( )
A.(5,10) B.(6,6)
C.(10,5) D.(7,2)
1.已知a>0,b>0,a+b=1,则+的取值范围是( )
A.(2,+∞) B.[2,+∞)
C.(4,+∞) D.[4,+∞)
21.( 14分)已知函数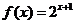 定义在R上.
定义在R上.
(1)若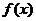 可以表示为一个偶函数
可以表示为一个偶函数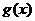 与一个奇函数
与一个奇函数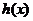 之和,设
之和,设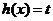 ,
,
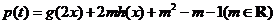 ,求出
,求出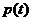 的解析式;
的解析式;
(2)若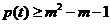 对于
对于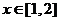 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(3)若方程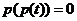 无实根,求m的取值范围.
无实根,求m的取值范围.
20.( 13分)设函数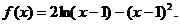
(1)求函数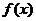 的单调递增区间;
的单调递增区间;
(2)若关于x的方程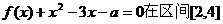 内恰有两个相异的实根,
内恰有两个相异的实根,
求实数a的取值范围。
19.( 12分)已知函数f (x)=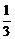 x3+
ax2-bx (a, b∈R) .
x3+
ax2-bx (a, b∈R) .
(1)若y=f (x)图象上的点(1,-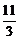 )处的切线斜率为-4,求y=f (x)的极大值;
)处的切线斜率为-4,求y=f (x)的极大值;
(2)若y=f (x)在区间[-1,2]上是单调减函数,求a + b的最小值.
18.(12分)已知函数f(x)对任意实数x,y满足f(x)+f(y)=f(x+y)+3,f(3)=6,当x>0时,f(x)>3.
(1)判断f(x)在R上的单调性,并证明你的结论.
(2)是否存在实数a使f (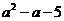 )<4成立?若存在求出实数a;若不存在,则说明理由.
)<4成立?若存在求出实数a;若不存在,则说明理由.
17.(12分)某租赁公司拥有汽车100辆,当每辆月租金3000元时,可全部租出,当每辆车的月租金增加50元时,未租出的车将会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每辆每月需要保管费50元。
(1)当每辆车的月租金定为3600元时,能租出去多少辆车?
(2)每辆车的月租金定为多少元时,租赁公司的月收益最大?最大的月收益可达多少?
16.(12分)已知命题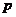 :方程
:方程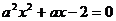 在[-1,1]上有解;命题
在[-1,1]上有解;命题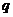 :只有一个
:只有一个
实数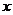 满足不等式
满足不等式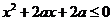 ,若命题“p或q”是假命题,求实数a的取值范围.
,若命题“p或q”是假命题,求实数a的取值范围.
15.符号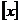 表示不超过
表示不超过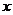 的最大整数,如
的最大整数,如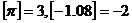 ,定义函数
,定义函数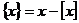 ,
,
那么下列命题中正确的序号是 .
(1)函数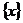 的定义域为R,值域为
的定义域为R,值域为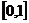 ; (2)方程
; (2)方程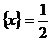 有无数解;
有无数解;
(3)函数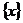 是周期函数; (4)函数
是周期函数; (4)函数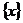 是增函数.
是增函数.
14.若函数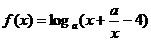 ,(
,(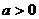 且
且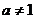 )的值域为R,则实数
)的值域为R,则实数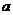 的取值范围是 __________________。
的取值范围是 __________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com