变式：设函数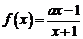，其中

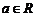
 m≥2或m≤－2.

所以，存在实数m，使不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈[-1，1]恒成立，其取值范围是{m|m≥2，或m≤－2}.

【点晴】利用导数研究函数的单调性和最值.在解决函数综合问题时要灵活运用数学思想和方法化归为基本问题来解决.

②                  或

       g(－1)=m²－m－2≥0      g(1)=m²+m－2≥0

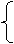
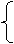      m>0，                m<0，

m≥2或m≤－2.

所以，存在实数m，使不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈[－1，1]恒成立，其取值范围是{m|m≥2，或m≤－2}.

方法二：

当m=0时，②显然不成立；

当m≠0时，

②  

         g(1)=m²+m－2≥0，

     g(－1)=m²－m－2≥0，

∵－1≤a≤1，∴|x₁-x₂|=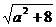≤3.

要使不等式m²+tm+1≥|x₁－x₂|对任意a∈A及t∈[－1，1]恒成立，

当且仅当m²+tm+1≥3对任意t∈[－1，1]恒成立，

即m²+tm－2≥0对任意t∈[－1，1]恒成立.        ②

设g(t)=m²+tm－2=mt+(m²－2)，

方法一：

∴          从而|x₁－x₂|==.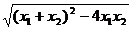

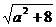x₁x₂=－2，

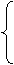             x₁+x₂=a，