
对任意满足xÎ(0,1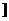 ,总存在n(nÎN),使得
,总存在n(nÎN),使得
<x≤,
根据(1)(2)结论,可知:
f(x)≤f()≤+2,
且2x+2>2´+2=+2,
(3)对一切xÎ(0,1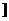 ,都有
,都有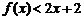 .
.
所以对一切nÎN,都有f()≤+2.
即f()≤+2.
又f()=f(1)=3≤2+,
故函数f(x)的最大值为3,最小值为2.
(2)解:在条件③中,令x1=x2=,得f()³2f()-2,即f()-2≤[f()-2],
故当nÎN*时,有f()-2≤[f()-2]≤[f()-2]≤???≤[f()-2]=,
(3)某人发现:当x=(nÎN)时,有f(x)<2x+2.由此他提出猜想:对一切xÎ(0,1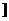 ,都有
,都有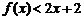 ,请你判断此猜想是否正确,并说明理由.
,请你判断此猜想是否正确,并说明理由.
解: (1)设0≤x1<x2≤1,则必存在实数tÎ(0,1),使得x2=x1+t,
由条件③得,f(x2)=f(x1+t)³f(x1)+f(t)-2,
∴f(x2)-f(x1)³f(t)-2,
由条件②得, f(x2)-f(x1)³0,
故当0≤x≤1时,有f(0)≤f(x)≤f(1).
又在条件③中,令x1=0,x2=1,得f(1)³f(1)+f(0)-2,即f(0)≤2,∴f(0)=2,
(2)试比较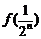 与
与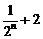 的大小
的大小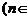 N);
N);
(1)试求函数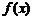 的最大值和最小值;
的最大值和最小值;
【范例3】已知函数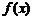 的定义域为
的定义域为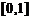 ,且同时满足:①
,且同时满足:①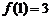 ;②
;②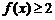 恒成立;③若
恒成立;③若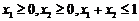 ,则有
,则有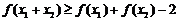 .
.
故当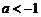 时,
时,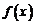 在区间
在区间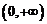 上是单调减函数。
上是单调减函数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com