
江西省吉安市2009届高三第一次模拟考试
理 科 数 学
吉安一中 贺姓芳
命题人: 审校:吉安市教研室 杜小许
吉水二中 王跃兴
本试卷第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至4页,共150分.
第Ⅰ卷
考生注意:
1、答题前,考生务必将自己的准考证号。姓名填写在答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。
2、第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.第Ⅱ卷用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
3、考试结束,监考员将试题卷、答题卡一并收回。
参考公式:
如果事件 、
、 互斥,那么 球的表面积公式
互斥,那么 球的表面积公式


如果事件 、
、 相互独立,那么 其中
相互独立,那么 其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件A在一次试验中发生的概率是 ,那么
,那么 
 次独立重复试验中恰好发生
次独立重复试验中恰好发生 次的概率 其中
次的概率 其中 表示球的半径
表示球的半径

一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知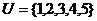 ,
,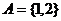 ,
,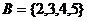 ,则
,则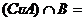
A.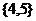 B.
B.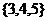 C.
C.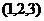 D.
D.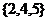
2.已知数列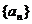 为等差数列,且
为等差数列,且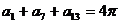 ,则
,则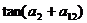
A. B.
B.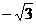 C.
C.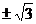 D.
D.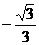
3.设函数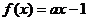 ,且
,且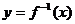 的图象过点
的图象过点 ,则
,则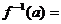
A.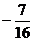 B.
B.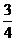 C.
C.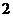 D.
D.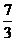
4.将函数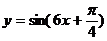 的图象上各点的横坐标伸长到原来的
的图象上各点的横坐标伸长到原来的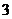 倍,再向右平移
倍,再向右平移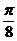 个单位,得到的函数的一个对称中心是
个单位,得到的函数的一个对称中心是
A.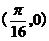 B.
B.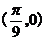 C.
C.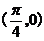 D.
D.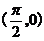
5.复数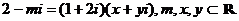 ,且
,且 ,则
,则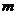 的值
的值
A.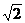 B.
B.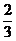 C.-
C.-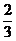 D.
D.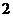
6.设二项式 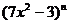 的展开式中各项系数之和为
的展开式中各项系数之和为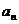 ,二项式
,二项式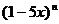 的展开式中各项的二项式系数之和为
的展开式中各项的二项式系数之和为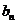 ,且点
,且点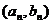 在直线
在直线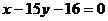 上,则
上,则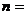
A.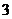 B.
B. C.
C.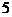 D.
D.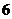
7 一个棱锥被平行于底面的截面截成一个小棱锥(记为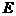 )和另一个几何体(记为
)和另一个几何体(记为 ),若
),若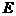 的体积为
的体积为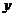 ,
, 的体积为
的体积为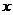 ,则
,则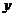 关于
关于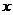 的函数图象大致形状为
的函数图象大致形状为

8.若方程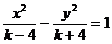 表示双曲线,则它的焦点坐标为
表示双曲线,则它的焦点坐标为
A.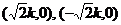 B.
B.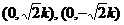
C.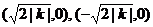 D.由
D.由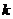 决定
决定
9已知直线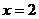 及
及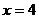 与函数
与函数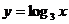 的图象的交点分别为
的图象的交点分别为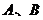 ,与函数
,与函数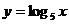 的图象的交点分别为
的图象的交点分别为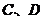 ,则直线
,则直线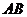 与
与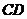
A.平行 B.相交且交点在第二象限
C.相交且交点在第三象限 D.相交且交点是原点
 ≥
≥
10.设二元一次不等式组所  ≥
≥ 表示的平面区域为
表示的平面区域为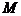 ,使函数
,使函数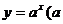
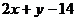 ≤
≤
 的图象过区域
的图象过区域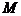 的
的 的取值范围是
的取值范围是
A. B.
B.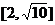 C.
C. D.
D.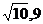
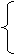
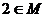
11.已知 ,且
则
,且
则 的取值范围是
的取值范围是

A.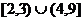 B.
B.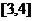 C.
C.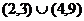 D.
D.
12.连续掷骰子两次得到的点数分别为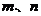 ,作向量
,作向量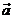
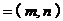 ,则与向量
,则与向量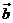
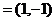 的夹角成为直角三角形内角的概率是
的夹角成为直角三角形内角的概率是
A.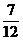 B.
B.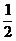 C.
C.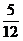 D.
D.
吉安市高三第一次模拟考试
理 科 数 学
第Ⅱ卷
注意事项:
第Ⅱ卷2页,须用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
二、填空题:本大题共4小题,每小题4分,共16分。请把答案填在答题卡上。
13.设随机变量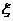 ~
~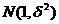
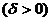 ,若
,若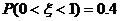 ,则
,则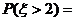 _______。
_______。
14.数列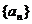 为
为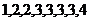 …则此数列的第
…则此数列的第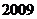 项
项 _______________。
_______________。
15.已知点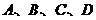 在同一个球面上,
在同一个球面上,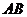
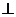 平面
平面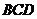 ,
,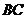
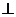
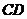 ,若
,若
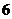 ,
,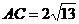 ,
, ,则
,则 两点间的球面距离是_______________。
两点间的球面距离是_______________。
16.给出下列命题:
①不存在实数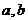 使
使 的定义域、值域均为一切实数;
的定义域、值域均为一切实数;
②函数 图象与函数
图象与函数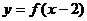 图象关于直线
图象关于直线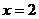 对称;
对称;
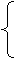
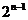
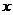 ≥
≥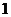
③函数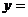 是
是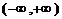 上的连续函数;
上的连续函数;
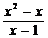
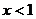
④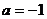 是方程
是方程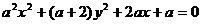 表示圆的充分必要条件.
表示圆的充分必要条件.
其中真命题的序号是______________________。(写出所有真命题的序号)
三、解答题:本大题共6小题,共74分。解答应写出必要的文字说明,证明过程或演算步骤。
17.(本小题满分12分)
已知向量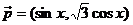 ,
,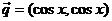 ,定义函数
,定义函数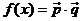
(1)求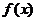 的最小正周期
的最小正周期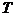 ;
;
(2)若 的三边长
的三边长 成等比数列,且边
成等比数列,且边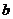 所对角
所对角 的取值集合为
的取值集合为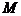 ,则当
,则当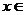
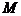 时,求函数
时,求函数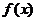 的最大值。
的最大值。
18.(本小题满分12分)
等差数列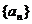 的公差不为零,
的公差不为零,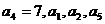 成等比数列,数列
成等比数列,数列 满足:
满足:
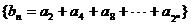
(1)求数列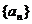 、
、 的通项公式;
的通项公式;
(2)若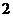 ≤
≤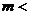
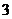 ,求
,求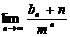
19.(本小题满分12分)
一个盒子装有完全相同的6张卡片,上面分别写着如下6个定义域均为R的函数:
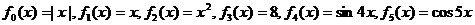 。
。
(1)从盒子中随机取出2张卡片,将卡片上的两个函数相加得一个新的函数,求所得函数是偶函数的概率;
 (2)从盒子中不放回地取卡片,每次取出一张,直至写有奇函数的卡片被全部取出为止,求抽取次数
(2)从盒子中不放回地取卡片,每次取出一张,直至写有奇函数的卡片被全部取出为止,求抽取次数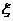 的数学期望。
的数学期望。
20.(本小题满分12分)
如图,在直四棱柱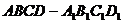 中,
中,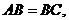
 为
为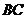 中点,点
中点,点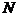 在
在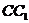 上。
上。
(1)试确定点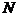 的位置,使
的位置,使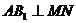 ;
;
(2)当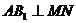 时,求二面角
时,求二面角 的大小。
的大小。
 21.(本小题满分12分)
21.(本小题满分12分)
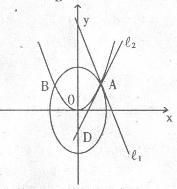
已知椭圆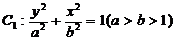 与抛物线
与抛物线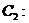
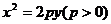 的交点分别为
的交点分别为 ,如图所示,
,如图所示,
椭圆和抛物线在点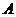 处的切线分别为
处的切线分别为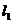 和
和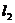 ,且斜
,且斜
率为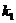 和
和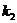
(1)当 为定值时,求证:
为定值时,求证: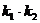 为定值(与
为定值(与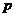 无关);
无关);
(2)设 且
且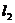 与
与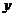 轴的交点为
轴的交点为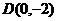 ,求
,求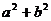 的最小值和此时椭圆的方程。
的最小值和此时椭圆的方程。
22.(本小题满分14分)
设函数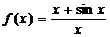
(1)判断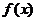 在区间
在区间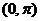 上的增减性并证明之;
上的增减性并证明之;
(2)若不等式 ≤
≤ ≤
≤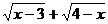 对一切
对一切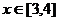 恒成立。
恒成立。
①求实数 的取值范围;
的取值范围;
②设 ≤
≤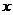 ≤
≤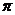 ,求证:
,求证: ≥
≥
吉安市高三第一次模拟考试理科数学试卷
一、选择题(5分×12=60分)
B B D D C B B D D C A A
二、填空题(4分x 4=16分)
13.0.1
14.63
15. 16.①③
16.①③
三、解答题(12分×5+14分=74分)
17.解:(1) 2分
2分
 ……………………4分
……………………4分
 ∴
∴ 的最小正周期为
的最小正周期为 …………………6分(2)∵
…………………6分(2)∵ 成等比数列 ∴
成等比数列 ∴
∴ ≥
≥ ………………………8分
………………………8分
∵ ∴
∴

 ≤
≤ 即
即
 ≤
≤

∵ ∴
∴ ≤
≤ ………………………………………………10分
………………………………………………10分
18.解:(1)设 公差
公差 由
由 成等比数列得
成等比数列得 …………………1分
…………………1分
∴即 ∴
∴ 舍去或
舍去或 …………………………3分
…………………………3分
∴ ………………………………………………4分
………………………………………………4分
又 ………………………………………………5分
………………………………………………5分
∴
 ………………………………………7分
………………………………………7分
(2) ………………………………………………8分
………………………………………………8分
当 时,
时, ………………………………………10分
………………………………………10分
当 时,
时, …………………………7分
…………………………7分
19.解:(1)记“任取2张卡片,将卡片上的函数相加得到偶函数”为事件A,
 ……………………………………………………4分
……………………………………………………4分
(2) 可能值为
可能值为 ……………………………………………………………5分
……………………………………………………………5分

 …………………………10分
…………………………10分
∴ …………………………12分
…………………………12分
20.解:(1)连结

 为正△
…1分
为正△
…1分






 面
面
 3分
3分
面 面
面



即点 的位置在线段
的位置在线段 的四等分点且靠近
的四等分点且靠近 处 ………………………………………6分(2)过
处 ………………………………………6分(2)过 作
作 于
于 ,连
,连
 由(1)知
由(1)知 面
面 (三垂线定理)
(三垂线定理)
∴ 为二面角
为二面角 的平面角……9分
的平面角……9分




在 中,
中,
在 中,
中,
∴二面角 的大小为
的大小为 ………………………………………12分
………………………………………12分
(说明:若用空间向量解,请参照给分)
 21.解:(1)设
21.解:(1)设 ,由
,由 取
取 得
得


则 ……………………2分
……………………2分
∴ …………………………12分
…………………………12分
又∵ 为定值,
为定值, 则
则 ………………5分
………………5分
∵ 为定值,∴
为定值,∴ 为定值。
为定值。
(2)∵ ,∴抛物线方程为:
,∴抛物线方程为: 设点
设点 则
则
由(1)知 则
则 ………………………………8分
………………………………8分
又∵ 过点
过点 ∴
∴ ∴
∴ ∴
∴ ………………………………9分
………………………………9分
代入椭圆 方程得:
方程得:
∴ ≥
≥ ………………11分
………………11分




当且仅当 即 上式取等号


∴此时椭圆的方程为: ………………………………………12分
………………………………………12分
22.解:(1)∵  ∴
∴ …1分
…1分
设
 则
则 ……2分
……2分
∴ 在
在 上为减函数 又
上为减函数 又
 时,
时,
 ,∴
,∴ ∴
∴ 在
在 上是减函数………4分(2)①∵
上是减函数………4分(2)①∵ ∴
∴ 或
或 时
时
 ∴
∴ …………………………………6分
…………………………………6分
 又≤
又≤ ≤
≤ 对一切
对一切 恒成立
∴
恒成立
∴ ≤
≤ ≤
≤ ……………8分
……………8分
②显然当 或
或 时,不等式成立
…………………………9分
时,不等式成立
…………………………9分
当 ,原不等式等价于
,原不等式等价于 ≥
≥ ………10分
………10分
下面证明一个更强的不等式: ≥
≥ …①
…①
即 ≥
≥ ……②亦即
……②亦即 ≥
≥ …………………………11分
…………………………11分
由(1) 知 在
在 上是减函数 又
上是减函数 又 ∴
∴ ……12分
……12分
∴不等式②成立,从而①成立 又

∴ >
>
综合上面∴ ≤
≤ ≤
≤ 且
且 ≤
≤ ≤
≤ 时,原不等式成立 ……………………………14分
时,原不等式成立 ……………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com