
题目列表(包括答案和解析)
3.计算公式: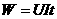 国际单位:J,常用单位:度。
国际单位:J,常用单位:度。
2.意义:反映了电路消耗电能的多少,即把电能转化为其它形式的能的多少。
1.定义:电荷在电场力的作用下运动,电场力会对电荷做功,把电场力做的功简称电功,又称电流做的功。
3.关于导体的伏安特性曲线:注意横纵坐标的意义。
|

例1. 一个电阻元件两端电压是1.5V时,通过它的电流是4.5mA,如果这个电阻元件两端加的电压为24V时,20秒内有多少电子通过这个电阻器。
解析:由题意可知,电阻器的电阻是不变的,设为R。通过欧姆定律及U1=1.5V,I1=4.5mA即可求得电阻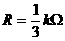 。再用欧姆定律又可求出
。再用欧姆定律又可求出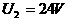 时,通过电阻器的电流为
时,通过电阻器的电流为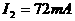
 从电流的定义出发通过导体的电量
从电流的定义出发通过导体的电量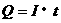 可求得20s内通过电阻器的电量Q,每个电子所带电量
可求得20s内通过电阻器的电量Q,每个电子所带电量 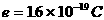 可求得通过导体的电子数n。
可求得通过导体的电子数n。
当然考虑到对同一个电阻元件用欧姆定律可以用比例法求解,这样可能会简单一些。
根据欧姆定律有
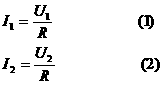
(1)式除以(2)式得 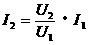
电流的定义 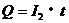
得 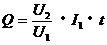
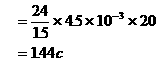
通过的电子数
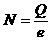
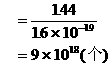
变式训练1: 某电解池,如果1s内共有5×1018个二价正离子和1×1019个一价负离子通过某截面,那么通过这个截面的电流是( )
A.0A B.0.8A C.1.6A D.3.2A
答D
例2. 两根完全相同的金属导线,如果把其中的一根均匀拉长到原来的4倍,把另一根导线对折后绞合起来,则它们的电阻之比为: 。
解析:解析:金属导线原来的电阻为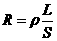 拉长后l1=4l,因为总体积V=LS保持不变,所以截面积
拉长后l1=4l,因为总体积V=LS保持不变,所以截面积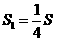 ,
,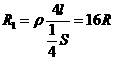
对折后L2=L/2,截面积S2=2S ∴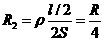
则后来两导线的电阻之比R1:R2=64:1
点评:某一导体形状改变后,讨论其电阻变化要抓住要点(1)电阻率不变;(2)总体积不变。
|
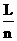 ,再拉长至L,则导线电阻变为( )
,再拉长至L,则导线电阻变为( )
A.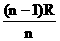 B.
B.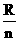 C.
C.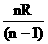 D.Nr
D.Nr
 答案:C
答案:C
例3. 如图10-1-2所示的I--U图象对应的两个导体:
①电阻之比R1:R2= ;
②若两导体中的电流相等(不为0)时,电压之比U1:U2= ;
③若两导体中的电压相等(不为0)时,电流之比I1:I2= .
解析:(1)在I-U图象中为直线斜率 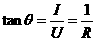 ,
故
,
故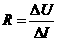 ,于是得,
,于是得,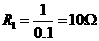 ,
, 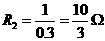 , 故R1:R2=3:1
, 故R1:R2=3:1
(2)由欧姆定律可得U=IR,当I相同时,U∝R,故U1 :U2=R1:R2=3:1 
(3)根据欧姆定律:I=U/R,当U相同时,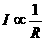 ,故I1:I2=R2:R1=1:3.也可由图象直接得出
,故I1:I2=R2:R1=1:3.也可由图象直接得出
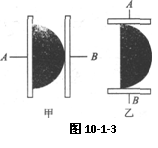 变式训练3:如图10-1-3所示,P为一块均匀的半圆形合金片将它按图甲的方式接在A、B之间时,测得它的电阻为R,若将它按图乙的方式接在A、B之间时.这时的电阻应是( )
变式训练3:如图10-1-3所示,P为一块均匀的半圆形合金片将它按图甲的方式接在A、B之间时,测得它的电阻为R,若将它按图乙的方式接在A、B之间时.这时的电阻应是( )
A.R B.2R
C.3R D.4R
答:D(点拨:甲图等效为2个四分之一圆导体的并联,乙图等效为2个四分之一圆导体的串联)
第2课时 电功和电热
|

2.欧姆定律的应用:注意电压、电流、电阻的同一性。
1.电阻定律的应用:在讨论导体形变引起电阻变化时要注意导体体积通常不变。
3.对于金属、电解液在不考虑温度的影响时其伏安特性曲线是过原点的倾斜的直线,这样的导体叫线性导体,否则为非线性导体。
|

2.意义:斜率的倒数表示电阻。
1.定义:导体的电流随电压变化的关系曲线叫做伏安特性曲线。如图10-1-1
3.适用条件:金属或电解液导电。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com