1.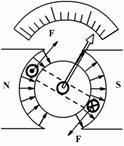如图11-5-1所示，安培力对转轴产生力矩M₁和弹簧的扭转力矩M₂平衡.导线所处位置磁感强度大小为B，线框长为L、宽为d、匝数为n，当线圈中通有电流I，

M₁=F·d　　　　　　　　　 　图11-5-1

F=nBIL

M₂ =kθ

则有M₁=M₂

即I=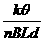

5.应用一些必要的数学知识，画出粒子的运动轨迹图，根据题目的条件和问题灵活选择不同的物理规律解题。一般思路有两类:1.力和运动角度思考 2.动量和能量的角度思考

(1)当带电粒子在复合场中处于静止或者是做匀速直线运动时，应该从力的平衡的角度分析寻找突破口。

(2)当带电粒子在复合场中做匀加速直线运动时，可以考虑用牛顿运动定律。

(3)当带电粒子在复合场中做匀速圆周运动时，可以考虑应用牛顿第二定律结合圆周运动的相关规律求解。

(4)当带电粒子做复杂的曲线运动时，一般用动能定理或者是能量守恒规律求解。

(5)对以一些由于特殊状态(临界状态)所带来的临界问题，应该充分挖掘临界状态下的特点和隐含条件。如题目叙述中一些特殊词汇“恰好”“最大”“刚好”“至少”“最高”“最终”等往往是解题的突破口，列出相应的辅助方程。

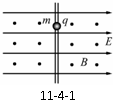例1.如图11-4-1所示，空间存在水平向右的匀强电场E和垂直纸面向外的匀强磁场B，一个质量为m、带电荷量为+q的小球套在不光滑的足够长的竖直绝缘杆上，从静止开始下滑。已知滑动摩擦系数为μ

(1)求下滑过程中小球具有的最大加速度a_m，并求此时的速度v

(2)求下滑过程中小球具有的最大速度v_m

解析：(1)小球运动分析：开始小球受重力、电场力、洛伦兹力、弹力和摩擦力，,随着速度增加，洛伦兹力增加，弹力减小，摩擦力减小；当速度增加到一定速度v时，洛伦兹力等于电场力，弹力和摩擦力都等于零，,此时加速度最大，此后，随着洛伦兹力增大，弹力向右，摩擦力又从零开始增加，加速度减小；当摩擦力增加至与重力平衡时，加速度为零，速度增加到最大值v_m，.

通过以上分析可知：当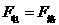时，加速度最大有: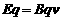　 　

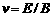
此时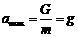 方向竖直向下

(2)当小球的加速度等于零时，速度最大v_m

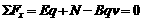..............①

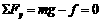...................②

又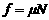　　　　 ..................③

由①②③得：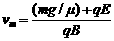

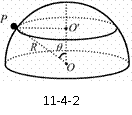变式训练1:如图11-4-2，一半径为R的光滑绝缘半球面开口向下，固定在水平面上。整个空间存在匀强磁场，磁感应强度方向竖直向下。一电荷量为q(q＞0)、质量为m的小球P在球面上做水平的匀速圆周运动，圆心为O^/。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0＜θ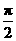＜)。为了使小球能够在该圆周上运动，求磁感应强度大小的最小值及小球P相应的速率。重力加速度为g.

解析：据题意，小球P在球面上做水平的匀速圆周运动，该圆周的圆心为O^／。P受到向下的重力mg、球面对它沿OP方向的支持力N和磁场的洛仑兹力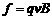①

根据牛顿第二定律有：

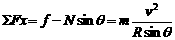......................②

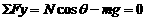　　　 .....................③

由①②③得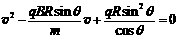：④

由于v是实数，必须满足：

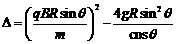................⑤

由此得： B≥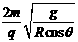......................⑥

可见，为了使小球能够在该圆周上运动，磁感应强度大小的最小值为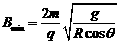.......⑦

此时，带电小球做匀速圆周运动的速率为：

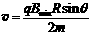　　　 ........................⑧

由⑦⑧式得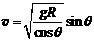：..............⑩)

例2．如图11-4-3，空间存在匀强电场和匀强磁场，电场方向为y轴正方向，磁场方向垂直于xy平面(纸面)向外，电场和磁场都可以随意加上或撤除，重新加上的电场或磁场与撤除前的一样．一带正电荷的粒子从P(x＝0，y＝h)点以一定的速度平行于x轴正向入射．这时若只有磁场，粒子将做半径为R₀的圆周运动；若同时存在电场和磁场，粒子恰好做直线运动．现在，只加电场，当粒子从P点运动到x＝R₀平面(图中虚线所示)时，立即撤除电场同时加上磁场，粒子继续运动，其轨迹与x轴交于M点．不计重力．求：

⑴粒子到达x＝R₀平面时速度方向与x轴的夹角以及粒子到x轴的距离；

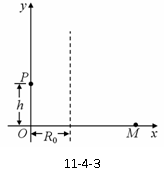⑵M点的横坐标x_M．

解析：

(1)设粒子质量、电荷量和入射速度分别为m、q和v₀，则电场的场强E和磁场的磁感强度B应满足下述条件：做直线运动有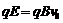：..................①

做圆周运动有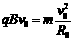：.........................②

只有电场时，粒子做类平抛，有：

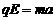　.....................................③

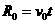　....................................④　　　　　

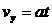　....................................⑤

由①②③④⑤解得：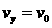

粒子速度大小为：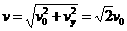

速度方向与x轴夹角为：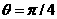

粒子与x轴的距离为：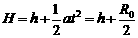

⑵撤电场加上磁场后，有：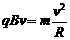

解得：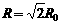

粒子运动轨迹如图所示，圆心C位于与速度v方向垂直的直线上，该直线与x轴和y轴的夹角均为π/4，有几何关系得C点坐标为：

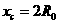
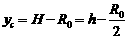
过C作x轴的垂线，在ΔCDM中：

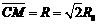
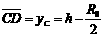
解得：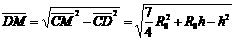

M点横坐标为：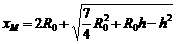

变式训练2：如图11-4-4所示，在坐标系Oxy的第一象限中存在沿y轴正方形的匀强电场，场强大小为E，在其它象限中存在匀强磁场，磁场方向垂直于纸面向里。A是y轴上的一点，它到坐标原点O的距离为h；C是x轴上的一点，到O点的距离为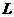，一质量为m、电荷量为q的带负电的粒子以某一初速度沿x轴方向从A点进入电场区域，继而通过C点进入磁场区域，并再次通过A点。此时速度方向与y轴正方向成锐角。不计重力作用。试求:

(1)粒子经过C点时速度的大小合方向；

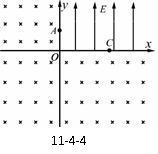(2)磁感应强度的大小B。

解析：

(1)以a表示粒子在电场作用下的加速度，有　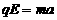 ...........................　 ①

加速度沿y轴负方向。设粒子从A点进入电场时的初速度为v₀，由A点运动到C点经历的时间为t，则有:　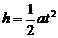 　........................　 ②

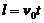　　 ............................... ③

由②③式得　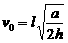 　...........................④

设粒子从点进入磁场时的速度为v，v垂直于x轴的分量v₁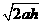 ...............................⑤　

v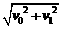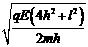＝＝ ................ ⑥

设粒子经过C点时的速度方向与x轴的夹角为α，则有

tanα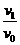＝　 .......................................................⑦

由④⑤⑦式得　 　........................⑧

(2)粒子经过C点进入磁场后在磁场中作速率为v的圆周运动。若圆周的半径为R，则有:

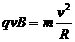　 ...............⑨

设圆心为P，则PC必与过C点的速度垂且有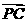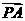＝＝R。用β表示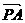与y轴的夹角，由几何关系得　 ....

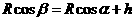.. ⑩

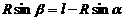　 ...................................... ⑾

由⑧⑩⑾式解得

R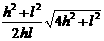＝ ...........................................⑿

由⑥⑨⑿式得

B＝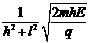

第5课时　 电磁场综合应用

4.如果粒子在运动过程中经过不同的区域受力发生改变，应根据需要对过程分阶段处理。

3.在正确的受力分析的基础上还要进行运动的分析，注意运动情况和受力情况的相互关联，特别要关注一些特殊的时刻所处的特殊状态(临界状态)。

2.正确的受力分析是解题的基础，处了重力、弹力、摩擦力以外，特别要注意电场力和洛伦兹力的分析，不可遗漏一个力。

1.认识粒子所在区域的场的组成，一般是电场、磁场、重力场三者的复合场，或者是其中两个的复合。

5.能量的转化和守恒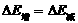

①分析在运动过程中有哪些形式的能量参与转化

②左边：看哪些能量增加了，增加了多少，然后把所有增加量相加

③右边：看哪些能量减少了，减少了多少，然后把所有减少量相加

解决带电粒子在复合场中运动问题的基本方法和思路：

4.动量守恒定律的应用

①应用条件:系统只有内部相互作用(系统不受外力或可以忽略不计),最典型的是碰撞过程。

②表达式：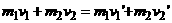

③注意动量矢量性，代入速度时要考虑其方向

3.动能定理的应用：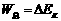

①表达式：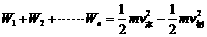

②左边：注意分析受力情况，有几个力做功，分别是正功还是负功，进行代数相加就是总功

③右边：一定要用末动能减去初动能

2.粒子做匀变速运动(a恒定)

牛顿第二定律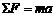：(力的合成)

或:取运动方向为x轴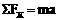,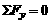(正交分解)