
题目列表(包括答案和解析)
2. 闭合电路欧姆定律,闭合电路中的电流、电动势、总电阻的关系,路端电压、电动势、电流、电源内阻的关系以及闭合电路中能量的转化。
1. 部分电路欧姆定律,包括六个基本物理量(电压、电流、电阻、电功、电功率、电热),三条定律(部分电路欧姆定律、电阻定律和焦耳定律),以及串、并联电路的特点等概念、定律的理解掌握和计算。
2.电源的效率:
η=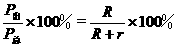
|

 例1.
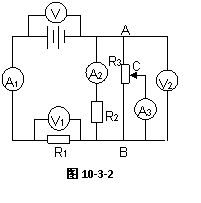
例1.  如图10-3-2所示,当滑动变阻器R3的滑片C向B方向移动时,电路中各电表示数如何变化?(电表内阻对电路的影响不计)
如图10-3-2所示,当滑动变阻器R3的滑片C向B方向移动时,电路中各电表示数如何变化?(电表内阻对电路的影响不计)
解析:滑动变阻器R3的滑片C向B方向移动时,外电路电阻增大,由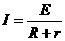 得总电流(I1)减小,电源内部降压
得总电流(I1)减小,电源内部降压 减小,由U=E-
减小,由U=E-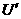 得路端电压U4增加,由U1=I R1得电阻R1电压U1减小,由U2=U4-U1得AB间电压U2增加,再由
得路端电压U4增加,由U1=I R1得电阻R1电压U1减小,由U2=U4-U1得AB间电压U2增加,再由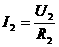 得R2支路电流I2增加,最后由I3=I1-I2得滑动变阻器中电流I3减小。
得R2支路电流I2增加,最后由I3=I1-I2得滑动变阻器中电流I3减小。
变式训练1:如图10-3-3,电源的内阻不可忽略.已知定值电阻R1=10Ω,R2=8Ω.当电键S接位置1时,电流表的示数为0.20A.那么当电键S接位置2时,电流表的示数可能是下列的哪些值
A.0.28A B.0.25A
C.0.22A D.0.19A
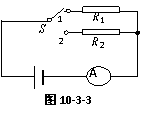
答案:C
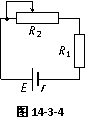 (提示:电键接2后,电路的总电阻减小,总电流一定增大,所以不可能是0.19A.电源的路端电压一定减小,原来路端电压为2V,所以电键接2后路端电压低于2V,因此电流一定小于0.25A.所以只能选C。)
(提示:电键接2后,电路的总电阻减小,总电流一定增大,所以不可能是0.19A.电源的路端电压一定减小,原来路端电压为2V,所以电键接2后路端电压低于2V,因此电流一定小于0.25A.所以只能选C。)
例2、 已知如图10-3-4,E =6V,
r =4Ω,R1=2Ω,R2的阻值变化范
围是0~10Ω。求:①电源的最大
输出功率;②R1上消耗的最大功
率;③R2上消耗的最大功率。
解析:①R2=2Ω时,外电阻等于内电阻,电源输出功率最大为2.25W;
②R1是定植电阻,电流越大功率越大,所以R2=0时R1上消耗的功率最大为2W;
③把R1也看成电源的一部分,等效电源的内阻为6Ω,所以,当R2=6Ω时,R2上消耗的功率最大为1.5W。
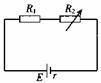
变式训练2、 如图10-3-5所示,R1为定值电阻,R2为可变电阻,E为电源电动势,r为电源内电阻,以下说法中正确的是( )
|
A.当R2=R1+r时,R2获得最大功率
B.当R1=R2+r时,R1获得最大功率
C.当R2=0时,R1上获得最大功率
D.当R2=0时,电源的输出功率最大
答案:AC(提示: 在讨论R2的电功率时,可将R1视为电源内阻的一部分,即将原电路等效为外电阻R2与电动势E、内阻为(R1+r)的电源(等效电源)连成的闭合电路(如图甲),R2的电功率是等效电源的输出功率.显然当R2=R1+r时,R2获得电功率最大,选项A正确;讨论R1的电功率时,由于R1为定值,根据P=IR知,电路中电流越大,R1上的电功率就越大(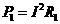 ),所以,当R2=0时,等效电源内阻最小(等于r)(如图乙),R1获得的电功率最大,故选项B错误,C正确;讨论电源的输出功率时,(R1+R2)为外电阻,内电阻r恒定,由于题目没有给出R1和r的具体数值,所以当R2=0时,电源输出功率不一定最大,故选项D错误. 答案AC正确。)
),所以,当R2=0时,等效电源内阻最小(等于r)(如图乙),R1获得的电功率最大,故选项B错误,C正确;讨论电源的输出功率时,(R1+R2)为外电阻,内电阻r恒定,由于题目没有给出R1和r的具体数值,所以当R2=0时,电源输出功率不一定最大,故选项D错误. 答案AC正确。)
第4课时 电路动态问题的分析
|

1.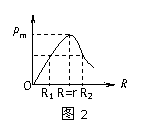 电源的输出功率:P出=IU=IE–I2r
电源的输出功率:P出=IU=IE–I2r
对于外电路是纯电阻的电路,电源的输出功率:
P出=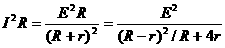
电源的输出功率随外电阻的变化关系如图10-3-1所示,
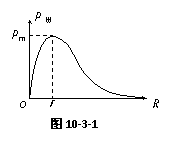
①当R=r时,P出max=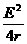
②一个输出功率(除最大功率外)P对应于两个不同的外电阻R1和R2,且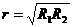 .
.
③当R<r时,R↑→P出↑;
当R>r时,R↑→P出↓.
3、两个关系:外电压等于外电路上串联的各分电压之和;总电流等于各支路电流之和。
2、局部电阻增则总电阻增,反之则总电阻减;支路数量增则总电阻减,反之则总电阻增。
闭合电路动态分析的基本思路是:“部分→整体→部分”,即从某个电阻的变化入手,由串并联规律先判断外电路总电阻的变化情况,然后由闭合电路欧姆定律判断总电流和路端电压的变化情况,最后由部分电路的欧姆定律判断各支路的电流、电压变化情况.
此类问题的分析要理解好以下三点:
1、理解闭合电路欧姆定律E=U外+Ir(E、r不变);部分电路欧姆定律U=IR。
4.纯电阻电路中,电源输出功率随外电路电阻而变化
P=UI=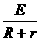 ·R·
·R·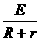 =
=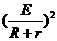 ·R
·R
|

3.内电路消耗功率(一定是发热功率):P内= I2r
2.外电路消耗功率(电源输出功率):P出= UI
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com