不同色光的频率与光的折射率有类似大小关系，通过折射光路知道折射率的关系，从而知道频率的关系，据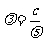知道真空中波长的关系，进而可以判断光电效应，干涉、衍射规律，反之根据干涉、衍射规律知道波长关系，从而据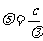知道频率关系，折射率关系，解决光电效应及折射问题.

典型例题

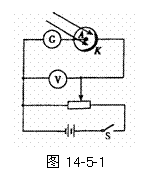
　 例1．某同学采用如图14-5-1所示的实验装置来研究光电效应现象.当用某一频率的光照射光电管的阴极K时，会发生光电效应现象，电流计中有电流通过.闭合电键S，在阳极A和阴极K之间加上反向电压，通过调节滑动变阻器的滑片逐渐增大电压，直至电流计中电流恰好为零，此时电压表的电压值称为反向截止电压，现用频率为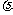的绿光照射阴极，测量到反向截止电压为U，设电子电量为e，普朗克常数为h，则：

　　　 A．逸出的电子的最大初动能为eU

　　　 B．阴极K的逸出功W=h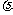－eU

　　　 C．如改用紫光照射，则光电子的最大初动能一定增加

　　　 D．如改用紫光照射，则阴极K的逸出功一定发生变化

解析：由光电效应实验得选项ABC正确

变式训练1.如图14-5-2所示，电路中所有元件完好，光照射到光电管上，灵敏电流计中没有电流通过，其原因可能是　　　 (　 )

A．入射光太弱

B．入射光波长太大

C．光照时间短

D．电源正负极接反

　　　　　　　　　　　　　　　 图14-5-2

解析：灵敏电流计中没有电流通，可能没有发生光电效应，也可能电源正负极接反，选项BD对

例2.小灯泡发光功率P＝1 W，能均匀向四周辐射出去，辐射出的光波波长为1.0×10^-7m，求在距离灯泡R＝10 km处每秒钟内投射到垂直于光线面积S＝1 m²上的光子数.

解析：小灯泡辐射的能量将均匀分布在以灯泡为球心的球面上.以灯泡为球心d＝10 km为半径的球面上每秒每平方米面积通过的光能为：

E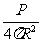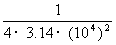＝＝＝7.96×10^-10J

每个光子的能量为

E₀＝hν＝h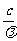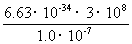＝＝1.99×10^-18J

故光子数：N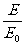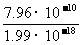＝＝＝4×10⁸ (个)

变式训练2.已经证明，1 s内进入一只眼睛瞳孔中波长为556nm的光子数57个时，我们就感到有光(眼睛对于这个波长的绿光最灵敏).设太阳向四周辐射的能量约有45%是可见光，若全部可见光光子的平均波长为556nm，在传播过程中没有能量损失，瞳孔直径为4 mm，那么距太阳多少光年的距离仍能看到太阳?(h＝6.63×10^-34J·s，太阳辐射总功率为3.8×10²⁶W)

解析：由题中已知条件，可知人眼能感觉到的最小能量为

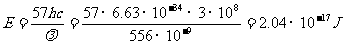
太阳辐射的总功率为3.8×10²⁶W，由题设条件知，其中45%是可见光的能量，那么每秒太阳向四周辐射的可见光能量为

E_总＝3.8×10²⁶×45%＝1.71×10²⁶J

设人到太阳的距离为R，人眼瞳孔的面积为S₀，则S₀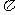＝r²，由能量分配关系可得：

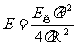
故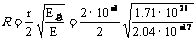

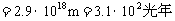
即距太阳3.1×10²光年的距离仍能看到太阳.

例3. 根据量子理论，光子具有动量，光子的动量等于光子的能量除以光速，即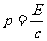，光照射到物体表面并被反射时，会对物体产生压强，这就是“光压”.光压是光的粒子性的典型表现.光压的产生机理如同气体压强：由大量气体分子与器壁的频繁碰撞产生了持续均匀的压力，器壁在单位面积上受到的压力就是气体的压强.

　(1)激光器发出的一束激光的功率为P_W，光束的横截面积为S.当该激光束垂直射在物体表面时，试计算单位时间内到达物体表面的光子的总动量.

　(2)若该激光束被物体表面完全反射，证明其在物体表面引起的光压是.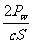

　(3)设想利用太阳的光压将物体送到太阳系以外的空间去，当然这只有当太阳对物体的光压超过了太阳对物体的引力才行.现如果用一种密度为1.0×10³ kg/m³的物体做成的平板，它的刚性足够大，则当这种平板厚度较小时，它将能被太阳的光压送出太阳系.试估算这种平板的厚度应小于多少?设平板处于地球绕太阳运动的公转轨道上，且平板表面所受的光压处于最大值，不考虑太阳系内各行星对平板的影响，已知地球公转轨道上的太阳常量为J=1.4×10³J/m²·s(即在单位时间内垂直辐射在单位面积上的太阳光的能量)，地球绕太阳公转的加速度为5.9×10^-3m/s².

解析：(1)设单位时间内激光器发出的光子数为n，每个光子的能量为E，动量为p₀，则激光器的功率为

P_w＝nE，

单位时间内到达物体表面的光子总动量为

p_总＝np₀＝n＝.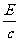

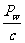(2)激光束被物体表面完全反射，故单位时间内的动量改变量为

Δp＝2p_总＝，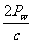

根据动量定理，激光束对物体表面的作用力为

F_m＝，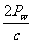

因此，激光束在物体表面引起的光压为

P＝.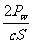

(3)设平板的质量为m，密度为ρ，厚度为d，面积为S₁，太阳常量为J，地球绕太阳公转的加速度为a.利用太阳的光压将平板送到太阳系以外的空间去，必须满足条件是太阳光对平板的压力大于太阳对其的引力.结合上问的结论，有:

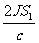>ma，

而平板的质量m＝ρdS₁，所以

d<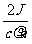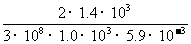＝＝1.6×10^-6m.

因此，平板的厚度应小于1.6×10^-6m.

变式训练3. 在彩色电视机的显像管中，从电子枪射出的电子在1.8×10⁴ V高压下加速，形成的平均电流为1 mA.

　(1)若电子撞击荧光屏后的速度为零，电子束对荧光屏的平均作用力是多大?

　(2)若电子撞击荧光屏时的能量全部转变为光能，而且产生的光均为波长为500 nm的绿光.已知荧光屏的面积为0.1 m²，则每秒钟在每平方厘米的荧光屏上平均产生多少个光子?

　(已知电子的质量m＝9.1×10^-31 kg，电子电量e＝1.60×10^-19 C，普朗克常量h＝6.63×10^-34 J·s)

解析：：(1)设电子经电场加速到达荧光屏时的速度为v，则有

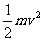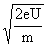eU＝，得v＝ ①

电子枪每秒发射的电子数n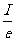＝，②

电子到达荧光屏时速度变为零，动量变化ΔP＝nmv.根据动量定理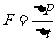得电子对荧光屏的平均冲力为F＝nmv ③

①②③联立得

F＝I·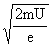＝10^-3×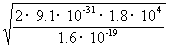N

＝4.5×10^-7 N.

(2)依题荧光屏每秒每平方厘米的光能为

W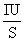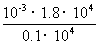＝＝J＝1.8×10^-2J，

每个光子的能量为

E＝hν＝h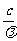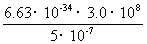＝J

＝3.978×10^-19J，

荧光屏每平方厘米面积上每秒产生的光子数为

n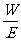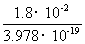＝＝个＝4.5×10¹⁶个

光学单元测试题

2.　　　 能量观点：据能量守恒分析球面辐射模型的能量分布特点.

1.　　　 动量观点：光子与物体的相互作用类似碰撞.可以根据动量定理研究冲力.

2．从微观角度理解光的波动性和粒子性

光既表现出波动性又表现出粒子性，很难用宏观世界的观念来认识，必须从微观的角度建立起光的行为图景，认识光的波粒二象性.需要明确的是：爱因斯坦光子说中的“粒子”和牛顿微粒说中的“粒子”是两个完全不相同的概念；同样，麦克斯韦电磁说中的“波”与惠更斯波动说中的“波”也是不同理论领域中完全不同的概念，其本质区别在于微观世界的认识与宏观世界的认识论的区别.

方法梳理

1.在双缝干涉实验中，光子通过双缝后，对某一个光子而言，其运动是不可预知的，但对大量光子而言，它们落在光屏上的位置又有规律性，即某些区域光子落点多，另一些区域光子落点少，落点多的区域就是亮条纹，落点少的区域就是暗条纹，因此说光波是一种概率波.

爱因斯坦光电效应方程式E_km＝h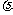－W中E_km是光电子的最大初动能，h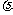是入射光子的能量，W叫做金属的逸出功，即从金属表面逸出时克服表面引力所做的功(消耗的能量)，极限频率满足：h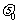=W，不同金属的W不同.因此不同金属发生光电效应的极限频率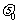不同.

3.照射光强度决定着单位时间内发射出的光电子数.

1.上面提到的入射光强度，指的是单位时间里入射在金属单位面积上的光子总能量，在入射光频率不变的情况下，光强与光子数成正比.换用不同频率的光，即使光强相同，光子数目也不同，因而逸出光电子数目也有区别.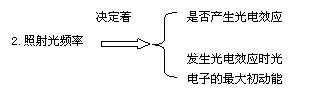

3.“电子云”的概念

在宏观领域中的“轨道”的概念在微观领域中是不适用的，玻尔理论中电子的轨道实际是电子出现概率大的地方，如果用疏密不同的点子表示电子在各个位置出现的概率，画出图来就像云雾一样，形象地称为电子云.在微观领域不能用“轨道”来描述粒子的运动，而应使用表示粒子出现概率大小的电子云来描述粒子的运动.

考点突破

2.牛顿力学的局限性

宏观物体，如果知道它在某一时刻的位置和速度以及受力情况，利用牛顿运动定律就可以预测它以后的位置和速度，即它的运动是可预测的.但对微观粒子，它以后的运动情况是不可预测的.

宏观物体，如果不受力作用，它将做匀速直线运动；微观粒子尽管不受力作用也不一定沿直线运动，例如电子在通过狭缝后就可能偏离直线运动的方向.对于微观粒子的运动，牛顿力学已经不适用了.

牛顿运动定律只适用于宏观低速物体，能量守恒定律、动量守恒定律既适用于宏观，也适用于微观，是自然界普遍遵循的规律，注意在分析问题时，一定要注意规律所适用的范围.