
题目列表(包括答案和解析)
17.(本小题满分13分)
若函数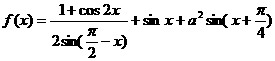 的最大值为
的最大值为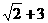 ,试确定常数a
,试确定常数a
的值.
16.已知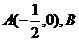 是圆
是圆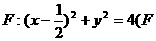 为圆心)上一动点,线段AB的垂直平
为圆心)上一动点,线段AB的垂直平
分线交BF于P,则动点P的轨迹方程为 .
解:由题意可知,动点P的轨迹是椭圆,这个椭圆的焦点是A(-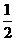 ,0)和F(
,0)和F(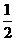 ,0),定长2a=圆F的半径2,因而动点P的轨迹方程为
,0),定长2a=圆F的半径2,因而动点P的轨迹方程为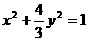
15.若10把钥匙中只有2把能打开某锁,则从中任取2把能将该锁打开的概率为 .
解;P=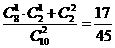
14.若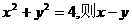 的最大值是
.
的最大值是
.
解:令x=2cosα,y=2sinα,则x-y=2cosα-2sinα=2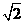 sin(
sin(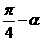 )≤2
)≤2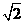 ,∴若
,∴若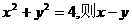 的最大值是2
的最大值是2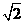
13.已知 均为锐角,且
均为锐角,且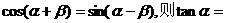 .
.
解:由已知得1-tanαtanβ=tanα-tanβ,∴tanα=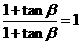 .
.
12.曲线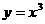 在点(1,1)处的切线与x轴、直线
在点(1,1)处的切线与x轴、直线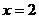 所围成的三角形的面积为
.
所围成的三角形的面积为
.
解:∵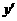 =3x2,∵在(1,1)处切线为y-1=3(x-1),令y=0,得切线与x轴交点(
=3x2,∵在(1,1)处切线为y-1=3(x-1),令y=0,得切线与x轴交点(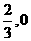 ),切线与直线x=2交于(2,4),∴曲线
),切线与直线x=2交于(2,4),∴曲线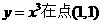 处的切线与x轴、直线
处的切线与x轴、直线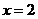 所围成的三角形的面积为S=
所围成的三角形的面积为S=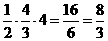 ..
..
11.若集合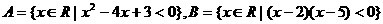 ,则
,则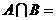
.
解:∵A=(-4,3),B=(2,5),∴A∩B={x|2<x<3}
9.若动点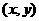 在曲线
在曲线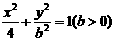 上变化,则
上变化,则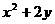 的最大值为 ( )
的最大值为 ( )
A.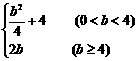 B.
B.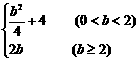
C.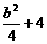 D.
D.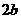
解:由题意可设x=2cosα,y=bsinα,则x2+2y=4cos2α+2bsinα=-4sin2α+2bsinα+4
=-2(sin2α-bsinα-2)=-2(sinα-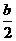 )2+4+
)2+4+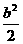 ,∴
,∴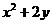 的最大值为
的最大值为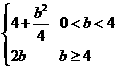 ,选(A)
,选(A)
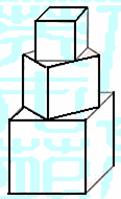 10.有一塔形几何体由若干个正方体构成,构成方式如图所
10.有一塔形几何体由若干个正方体构成,构成方式如图所
示,上层正方体下底面的四个顶点是下层正方体上底面
各连接中点,已知最底层正方体的棱长为2,且该塔形
的表面积(含最底层正方体的底面面积)超过39,则
该塔形中正方体的个数至少是 ( )
A.4 B.5
C.6 D.7
解:k层塔形的各层立方体的边长,增加的表面积以及k层塔形的
表面积一览表如下:
|
第k个立方体边长ak |
a!=2 |
a2=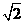 |
a3=1 |
a4=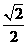 |
a5= 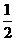 |
a6= 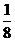 |
|
第k层立方体增加的面积bk |
b1=24 |
b2=8 |
b3=4 |
b4=2 |
b5=1 |
b6=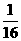 |
|
K层塔形的表面积Sk |
S1=24 |
S2=32 |
S3=36 |
S4=38 |
S5=39 |
S6= |
由上表可以看出要使塔形的表面积(含最底层正方体的底面面积)超过39,则
该塔形中正方体的个数至少是6层,选(C)
8.若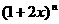 展开式中含
展开式中含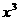 的项的系数等于含x的项的系数的8倍,则n等于 ( )
的项的系数等于含x的项的系数的8倍,则n等于 ( )
A.5 B.7 C.9 D.11
解: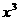 的项的系数为
的项的系数为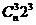 ,x的项的系数为
,x的项的系数为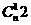 ,由题意得
,由题意得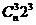 =8
=8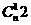 解之得n=5,选(A)一了
解之得n=5,选(A)一了
7.对于不重合的两个平面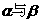 ,给定下列条件:
,给定下列条件:
①存在平面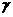 ,使得α、β都垂直于
,使得α、β都垂直于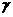 ;
;
②存在平面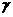 ,使得α、β都平行于
,使得α、β都平行于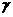 ;
;
③存在直线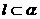 ,直线
,直线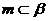 ,使得
,使得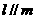 ;
;
④存在异面直线l、m,使得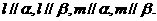
其中,可以判定α与β平行的条件有 ( )
A.1个 B.2个 C.3个 D.4个
解:命题①③是真命题,选(B)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com