
题目列表(包括答案和解析)
1、若(x-1)0 =1,则( )
A.x≥1 ; B.x≤1; C.x≠1; D.x为任意实数
27、在平面直角坐标系中(单位长度:1cm), 、
、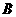 两点的坐标分别为
两点的坐标分别为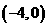 ,
,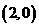 ,点
,点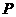 从点
从点 开始以2cm/s的速度沿折线
开始以2cm/s的速度沿折线 运动,同时点
运动,同时点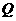 从点
从点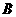 开始以1cm/s的速度沿折线
开始以1cm/s的速度沿折线 运动。
运动。
⑴在运动开始后的每一时刻一定存在以点 、
、 、
、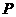 为顶点的三角形和以点
为顶点的三角形和以点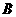 、
、 、
、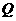 为顶点的三角形吗?如果存在,那么以点
为顶点的三角形吗?如果存在,那么以点 、
、 、
、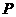 为顶点的三角形和以点
为顶点的三角形和以点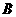 、
、 、
、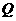 为顶点的三角形相似吗?以点
为顶点的三角形相似吗?以点 、
、 、
、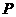 为顶点的三角形和以点
为顶点的三角形和以点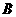 、
、 、
、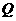 为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由。
为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由。
⑵试判断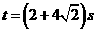 时,以点
时,以点 为圆心,
为圆心,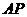 为半径的圆与以点
为半径的圆与以点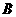 为圆心、
为圆心、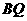 半径的圆的位置关系;除此之外
半径的圆的位置关系;除此之外 与
与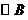 还有其他位置关系吗?如果有,请求出
还有其他位置关系吗?如果有,请求出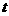 的取值范围。
的取值范围。
⑶请你选定某一时刻,求出经过三点 、
、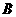 、
、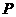 的抛物线的解析式。
的抛物线的解析式。
26、已知:抛物线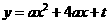 与
与 轴的一个交点为
轴的一个交点为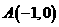 。
。
⑴求抛物线与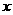 轴的另一个交点
轴的另一个交点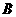 的坐标。
的坐标。
⑵点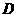 是抛物线与
是抛物线与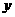 轴的交点,点
轴的交点,点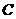 是抛物线上的一点,且以
是抛物线上的一点,且以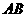 为一底的梯形
为一底的梯形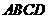 的面积为9,求此抛物线的解析式。
的面积为9,求此抛物线的解析式。
⑶点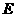 是第二象限内到
是第二象限内到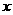 轴、
轴、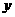 轴的距离的比为5:2的点,如果点
轴的距离的比为5:2的点,如果点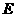 在⑵中的抛物线上,且它与点
在⑵中的抛物线上,且它与点 在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点
在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点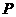 ,使
,使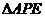 的周长最小?若存在,求出点
的周长最小?若存在,求出点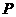 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
25、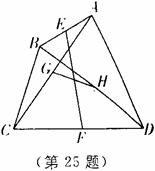 如图,已知四边形
如图,已知四边形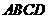 中,点
中,点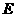 、
、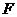 、
、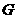 、
、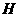 分别是
分别是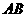 、
、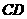 、
、 、
、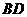 的中点,并且点
的中点,并且点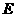 、
、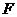 、
、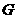 、
、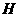 有在同一条直线上。
有在同一条直线上。
求证: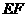 和
和 互相平分。
互相平分。
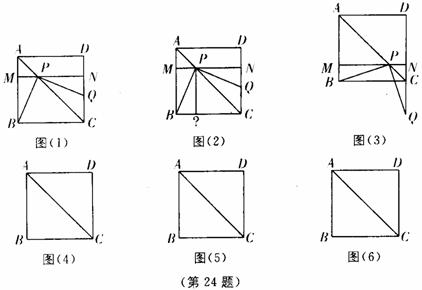
24、操作:将一把三角尺放在边长为1的正方形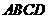 上,并使它的直角顶点
上,并使它的直角顶点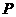 在对角线
在对角线 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点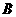 ,另一边与射线
,另一边与射线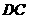 相交于点
相交于点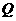 。
。
探究:设 、
、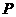 两点间的距离为
两点间的距离为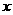 。
。
⑴当点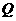 在
在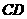 上时,线段
上时,线段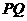 与线段
与线段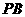 之间有怎样的大小关系?试证明你观察得到的结论(如图⑴)。
之间有怎样的大小关系?试证明你观察得到的结论(如图⑴)。
⑵当点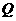 在边
在边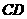 上时,设四边形
上时,设四边形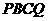 的面积为
的面积为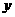 ,求
,求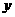 与
与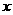 之间的函数解析式,并写出函数的定义域(如图⑵)。
之间的函数解析式,并写出函数的定义域(如图⑵)。
⑶当点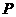 在线段
在线段 上滑动时,
上滑动时,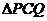 是否可能成为等腰三角形?如果可能,指出所有能使
是否可能成为等腰三角形?如果可能,指出所有能使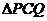 成为等腰三角形的点
成为等腰三角形的点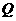 的位置,并求出相应的
的位置,并求出相应的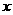 的值;如果不可能,试说明理由(如图⑶)。(图⑷、图⑸、图⑹的的形状、大小相同,图⑷供操作、实验用,图⑸和图⑹备用)
的值;如果不可能,试说明理由(如图⑶)。(图⑷、图⑸、图⑹的的形状、大小相同,图⑷供操作、实验用,图⑸和图⑹备用)
23、如图,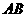 是
是 的弦,
的弦, 切
切 于点
于点 ,
,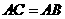 ,
,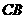 交
交 于点
于点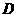 ,点
,点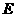 为弧
为弧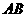 的中点,连结
的中点,连结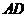 ,在不添加辅助线的情况下,
,在不添加辅助线的情况下,
⑴找出图中存在的全等三角形,并给出证明;
⑵图中存在你所学过的特殊四边形吗?如果存在,请你找出来并给出证明。
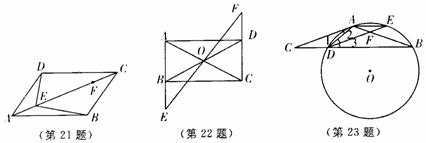
22、如图,矩形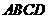 中,点
中,点 是
是 与
与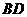 的交点,过点
的交点,过点 的直线与
的直线与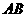 、
、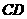 的延长线分别交于点
的延长线分别交于点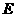 、
、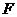 。
。
⑴求证: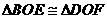 ;
;
⑵当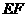 与
与 满足什么条件时,四边形
满足什么条件时,四边形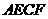 是菱形?并证明你的结论。
是菱形?并证明你的结论。
21、如图,在平行四边形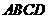 中,点
中,点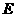 、
、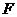 在对角线
在对角线 上,且
上,且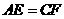 。请你以点
。请你以点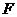 为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)。
为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的某一条线段相等(只需证明一组线段相等即可)。
⑴连结:___________;
⑵猜想:___________=__________;
⑶证明:______________。
20、已知方程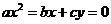 (
(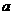 ,
,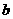 ,
,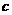 是常数),请你通过变形把它写成你所熟悉的一个函数表达式的形式,则函数表达式为______________,成立的条件是________,是_____________函数。
是常数),请你通过变形把它写成你所熟悉的一个函数表达式的形式,则函数表达式为______________,成立的条件是________,是_____________函数。
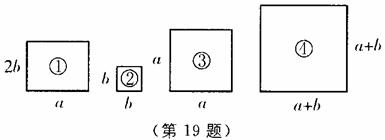
19、下列四个图形中,图①是长方形,图②、③、④是正方形。把图①、②、③三个图形拼在一起(不重合),其面积是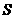 ,则
,则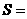 _________,图④的面积
_________,图④的面积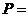 _________,则
_________,则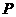 ________
________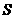 (填“>”“=”或“<”)。
(填“>”“=”或“<”)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com