
题目列表(包括答案和解析)
20.如图,在△ABC中,AB=15 cm,AC=12 cm,AD是∠BAC的外角平分线,
DE∥AB交AC的延长线于点E,那么CE=__________cm.

[提示]∠EAD=∠FAD=∠ADE,
∴ ED=AE=AC+CE.
再利用△ABC∽△EDC.
[答案]48.
[点评]本题要求灵活运用相似三角形的判定定理和性质.
19.如图∠CAB=∠BCD,AD=2,BD=4,则BC=__________.
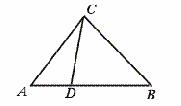
[提示]由△ABC∽△CBD,得BC2=BD·AB.
[答案]2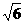 .
.
[点评]本题要求运用相似三角形的判定定理与性质.
18.如图,在矩形ABCD中,E是BC中点,且DE⊥AC,则CD︰AD=__________.
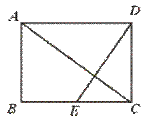
[提示]Rt△CDE∽Rt△DCA,并设AD为a,用a表示出EC和CD的长,或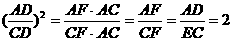 .
.
[答案]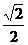 .
.
[点评]本题要求运用直角三角形的判定定理.
17.如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB延长线于点E,则△BAE相似于______.
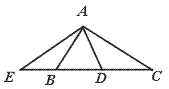
[提示]∠BAE=∠DAC=∠C.
[答案]△ACE.
[点评]本题要求灵活运用三角形相似的判定定理.
16.如图,已知DE∥BC,且BF∥EF=4︰3,则AC︰AE=__________.
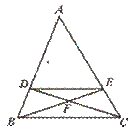
[提示]△BCF∽△EDF和△ABC∽△ADE构成两种基本图形.
[答案]4︰3.
[点评]本题要求运用三角形一边平行线的性质定理.
15.如图,l1∥l2∥l3,BC=3,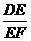 =2,则AB=___________.
=2,则AB=___________.
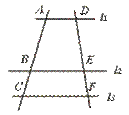
[提示]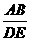 =
=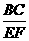 .
.
[答案]6.
[点评]本题要求运用平行线分线段成比例定理.
14.已知数3、6,再写出一个数,使这三个数中的一个数是另外两个数的比例中项,这个数是___________(只需填写一个数).
[提示]将b2=ac中任意两个字母用3、6代替,求出第三个字母所表示的数.
[答案]±12或±3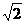 或±
或±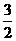 .
.
[点评]本题要求运用比例的有关概念.它是一道开放性问题,用数3、5、6代替不同字母,答数也就不同.
13.如果x︰y︰z=1︰3︰5,那么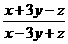 =___________.
=___________.
[提示]取x=1,y=3,z=5代入,或设x=k,则y=3k,z=5k.
[答案]-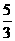 .
.
[点评]本题要求运用比例性质求值.
12.如图,将△ABC的高AD四等分,过每一个分点作底边的平行线,把三角形的面积分成四部分S1、S2、S3、S4,则S1︰S2︰S3︰S4等于……………………………( )
(A)1︰2︰3︰4 (B)2︰3︰4︰5 (C)1︰3︰5︰7 (D)3︰5︰7︰9
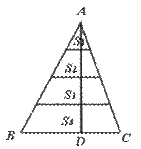
[提示]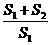 =(
=(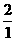 )2,
)2,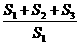 =(
=(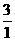 )2.
)2.
[答案]C.
[点评]本题要求运用相似三角形的面积比等于相似比的平方(即对应边上的高的比的平方).
11.如图,点A1、A2,B1、B2,C1、C2分别是△ABC的边BC、CA、AB的三等分点,且ABC的周长为l,则六边形A1A2B1B2C1C2的周长为…………………………( )
(A)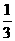 l (B)3l (C)2l (D)
l (B)3l (C)2l (D)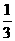 l
l
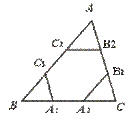
[提示]C1B2=A1A2=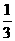 BC,B1A2=C1C2=
BC,B1A2=C1C2=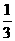 AB,A1C2=B1B2=
AB,A1C2=B1B2=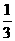 AC.[答案]D.
AC.[答案]D.
[点评]本题要求运用相似三角形的周长比等于相似比(即 对应边的比).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com