4．平面内两条不平行的线段必相交…………………………………………………(　)

[提示]仔细读题，想想线段的特征，线段有两个端点，有一定的长度，它们可以延长后相交，但本身可以既不平行，也不相交．

[答案]×．

[点评]平面内两条不平行的线段可以相交，也可以不相交，但平面内两条不平行的线段的延长线一定相交．

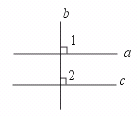
3．如果直线a⊥b，且b⊥c，那么a⊥c……………………………………………(　)

[提示]画图，a⊥b，则∠1＝90°，b⊥c，则∠2＝90°．

∴　∠1＝∠2．

∴　a∥c．

[答案]×．

[点评]由此题可知平面内垂直于同一直线的两直线互相平行，垂直关系没有传递性．

2．对顶角相等，但不互补；邻补角互补，但不相等…………………………………(　)

[提示]两直线互相垂直时，对顶角相等且互补，邻补角互补且相等．

[答案]×．

1．把一个角的一边反向延长，则可得到这个角的邻补角……………………………(　)

[提示]根据叙述，画出相应的图形即可判断．

[答案]√．

(五)证明题(每题6分，共24分)

27．已知：如图．AB∥CD，∠B＝∠C．求证：∠E＝∠F．

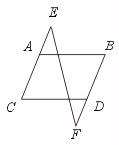
[提示]证明AC∥BD．

[答案]证明：∵　AB∥CD(已知)，

∴　∠B＝∠CDF(两直线平行，同位角相等)．

∵　∠B＝∠C(已知)，

∴　∠CDF＝∠C(等量代换)．

∴　AC∥BD(内错角相等，两直线平行)．

∴　∠E＝∠F(两直线平行，内错角相等)．

28．已知：如图，AC∥DE，DC∥EF，CD平分∠BCD．

求证：EF平分∠BED．

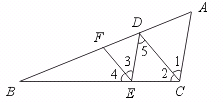
[提示]由AC∥DE．DC∥EF证∠1＝∠3．由DC∥EF证∠2＝∠4．再由CD平分∠BCA，即可证得∠3＝∠4．

[答案]证明：∵　AC∥DE(已知)，

∴　∠1＝∠5(两直线平行，内错角相等)．

同理∠5＝∠3．

∴　∠1＝∠3(等量代换)．

∵　DC∥EF(已知)，

∴　∠2＝∠4(两直线平行，同位角相等)．

∵　CD平分∠ACB，

∴　∠1＝∠2(角平分线定义)，

∴　∠3＝∠4(等量代换)，

∴　EF平分∠BED(角平分线定义)．

29．已知：如图，AB∥CD，∠1＝∠B，∠2＝∠D．求证：BE⊥DE．

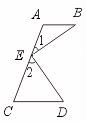
[提示]过点E作EF∥AB，证明∠BED＝90°．

[答案]证明：过点E作EF∥AB．

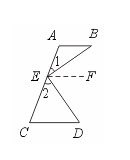∴　∠BEF＝∠B(两直线平行，内错角相等)．

∵　∠B＝∠1，

∴　∠BEF＝∠1(等量代换)．

同理可证：∠DEF＝∠2．

∵　∠1+∠BEF+∠DEF+∠2＝180°(平角定义)，

即2∠BEF+2∠DEF＝180°，

∴　∠BEF+∠DEF＝90°(等式性质)．

即∠BED＝90°．

∴　BE⊥DE(垂直的定义)．

30．已知：如图，AB∥CD，请你观察∠E、∠B、∠D之间有什么关系，并证明你所得的结论．

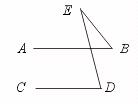
[提示]结论：∠B+∠E＝∠D．过点E作EF∥AB．

[答案]结论：∠B+∠E＝∠D．

证明：过点E作EF∥AB，

∴　∠FEB＝∠B(两直线平行，内错角相等)．

∵　AB∥CD，EF∥AB，

∴　EF∥CD(平行公理推论)，

∴　∠FED＝∠D(两直线平行，内错角相等)．

∵　∠FED＝∠FEB+∠BED＝∠B+∠BED，

∴　∠B+∠BED＝∠D(等量代换)．

本题还可添加如图所示的辅助线，请你证明∠B+∠E＝∠D．

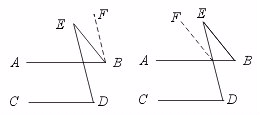
[点评]这是一道探索结论型的问题．要通过对直观图形仔细观察，大胆猜想，设定结论，再进行推理，验证结论．直观图形是观察思考的依据，准确的直观图形可引发正确的直觉思维．所以作图不可忽视．直觉思维是正确，还必须用相关的理论来验证．这样得到的结论方可靠．

23．如图，AB∥CD∥PN，∠ABC＝50°，∠CPN＝150°．求∠BCP的度数．

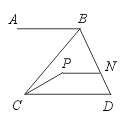
[提示]由AB∥CD，∠ABC＝50°可得∠BCD＝50°．

由PN∥CD，∠CPN＝150°，可得∠PCD＝30°．

∴　∠BCP＝∠BCD－∠PCD＝50°－30°＝20°．

[答案]20°．

24．如图，∠CAB＝100°，∠ABF＝110°，AC∥PD，BF∥PE，求∠DPE的度数．

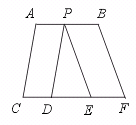
[提示]由AC∥PD，∠CAB＝100°，可得∠APD＝80°．

同理可求∠BPE＝70°．

∴　∠DPE＝180°－∠APD－∠BPE＝180°－80°－70°＝30°．

[答案]30°．

25．如图，DB∥FG∥EC，∠ABD＝60°，∠ACE＝36°，AP平分∠BAC．

求∠PAG的度数．

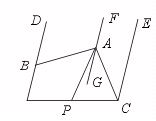
[提示]由DB∥FG∥EC，可得

∠BAC＝∠BAG+∠CAG

＝∠DBA+∠ACE

＝60°+36°＝96°．

由AP平分∠BAC得∠CAP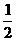＝∠BAC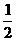＝×96°＝48°．

由FG∥EC得∠GAC＝ACE＝36°．

∴　∠PAG＝48°－36°＝12°．

[答案]12°．

26．如图，AB∥CD，∠1＝115°，∠2＝140°，求∠3的度数．

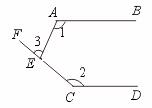
[提示]过点E作EG∥AB．

∵　AB∥CD由平行公理推论可得EG∥CD．

由此可求得∠AEC的度数．由平角定义可求得∠3的度数．

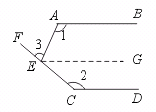
[答案]75°．

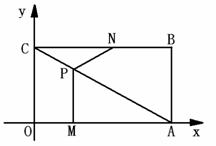
25．如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(4,0),(4,3).动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点M作MP⊥OA，交AC于P，连结NP。已知动点运动了x秒。

(1)P点的坐标为(　　　 ，　　　 )(用含x的代数式表示)；

(2)试求△NPC面积S的表达式，并求出面积S的最大值及相应的x值；

(3)当x为何值时，△NPC是一个等腰三角形？简要说明理由。

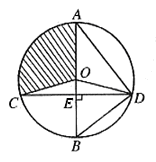
24、如图,已知的直径AB垂直于弦CD于E,连结AD、BD、OC、OD，且OD=5。

(1)　 若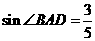，求CD的长；

(2)　 若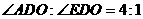，求扇形OAC(阴影部分)的面积(结果保留)

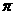23．在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S(次/分)是这个人年龄n(岁)的一次函数。

(1)根据以上信息，求在正常情况下，S关于n的函数关系式；

(2)若一位63岁的人在跑步，医生在途中给他测得10秒心跳为26次，问：他是否有危险？为什么？

22、(本小题满分5分)

已知反比例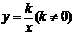函数和一次函数。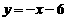

⑴ 若一次函数和反比例函数的图象交于点(－3，m)求m和k的值．

⑵ 当k满足什么条件时．这两个函数的图象有两个不同的交点？

⑶ 当k=－2时，设(2)中的两个函数图象的交点分别为 A、B，试判断A、B两点分别在第几象限，∠AOB是锐角还是钝角(只要求直接写出结论)．