
题目列表(包括答案和解析)
(四)计算题(每小题3分,共9分)
23.118°12′-37°37′×2.
[提示]先算乘,再求差.
[答案]42°58′.
计算过程如下:
118°12′-37°37′×2
=118°12′-75°14′
=117°72′-75°14′
=42°58′.
24.132°26′42″-41.325°×3.
[提示]将132°26′42″化成以“度”为单位的量再计算;
或将41.325°×3的积化成“度”、“分”、“秒”后再算.
[答案]解法一 132°26′42″-41.325°×3
=132.445°-123.975°
=8.47°.
解法二 132°26′42″-41.325°×3
=132°26′42″-123.975°
=132°26′42″-123°58′30″
=131°86′42″-123°58′30″
=8°28′12″.
[点评]在“度”、“分”、“秒”的混合运算中,若将“分”、“秒”化成度,则可将“度”“分”“秒”的计算转化成小数运算,免去繁杂的“进位”或“退位”.提高运算速度和正确率.
25.360°÷7(精确到分).
[提示]按四舍五入取近似值,满30″或超过30″即可进为1″.
[答案]约为51°26′.
计算过程如下:
360°÷7
=51°+3°÷7
=51°+25′+5′÷7
=51°+25′+300″÷7
≈51°+25′+43″
≈51°26′.
(三)选择题(每小题3分,共24分)
15.已知线段AB=10 cm,AC+BC=12 cm,则点C 的位置是在:①线段AB 上;②线段AB 的延长线上;③线段BA 的延长线上;④直线AB 外.其中可能出现的情况有………………………………………………………………………………( )
(A)0种 (B)1种 (C)2种 (D)3种
[提示]用数形结合的方式考虑.
[答案]D.
若点C在线段AB上,如下图,则AC+BC=AB=10 cm.与AC+BC=12 cm不合,故排除①.

若点C 在线段AB 的延长线上,如下图,AC=11 cm,BC=1 cm,则AC+BC=
11+1=12(cm),符合题意.

若点C 在线段BA 的延长线上,如下图,AC=1 cm,BC=11 cm,则AC+BC=
1+11=12(cm),符合题意.

若点C在直线AB外,如下图,则AC+BC=12(cm),符合题意.

综上所述:可能出现的情况有3种,故选D.
16.分别在线段MN的延长线和MN的反向延长线上取点P、Q,使MP=2NP.MQ=2MN.则线段MP 与NQ 的比是…………………………………………( )
(A)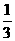 (B)
(B)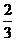 (C)
(C)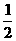 (D)
(D)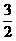
[提示]根据条件画出符合题意的图形,以形助思.
[答案]B.
根据题意可得下图:
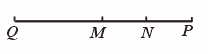
解法一:
∵ MP=2NP,
∴ N是MP的中点.
∴ MP=2MN.
∵ MQ=2MN,
∴ NQ=MQ+MN=2MN+MN=3MN.
∴ MP∶NQ=2MN∶3MN=2∶3=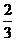 .
.
解法二:
设MN=x.
∵ MP=2NP,
∴ N是MP的中点.
∴ MP=2MN=2x.
∵ MQ=2MN=2x,
∴ NQ=MQ+MN=2MN+MN=3MN=3x.
∴ MP∶NQ=2MN∶3MN=2 x∶3 x=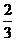 .
.
故选B.
17.一条直线可以将平面分成两部分,两条直线最多可以将平面分成四部分,三条直线最多可以将平面分成n 部分,则n 等于………………………………………( )
(A)6 (B)7 (C)8 (D)9
[提示]画图探索.
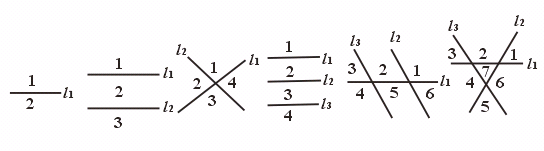
一条线 两条直线 三条直线
[答案]B.
[点评]平面内一条直线将平面分成两部分,记作a1=1+1=2;
平面内两条直线将平面最多分成四部分,记作a2=1+1+2=4;
平面内三条直线将平面最多分成七部分,记作a3=1+1+2+3=7;
平面内四条直线将平面最多分成几部分?由图可知,共可分成11个部分,记作a4=1+1+2+3+4=11.

若平面上有n条直线,最多可将平面分成多少部分,此时n条直线的相对位置如何?
从前面的分析不难推出平面上有n 条直线时,最多可将平面分成an=1+1+2+3+4+…+n=1+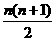 =
=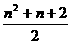 个部分,此时每两条直线都相交,且没有三条直线交于一点.
个部分,此时每两条直线都相交,且没有三条直线交于一点.
18.若互补两角有一条公共边,则这两个角的平分线所组成的角………………( )
(A)一定是直角 (B)一定是锐角
(C)一定是钝角 (D)是直角或锐角
[提示]分两种情况:①互补两角有公共顶点,有一条公共边没有重叠部分;②互补两角有公共顶点有一条公共边有重叠部分.
[答案]D.
如图:


19.已知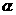 、
、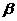 都是钝角,甲、乙、丙、丁四人计算
都是钝角,甲、乙、丙、丁四人计算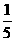
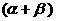 的结果依次是30°、
的结果依次是30°、
35°、60°、75°,其中恰有正确结果.这个正确结果是…………………( )
(A)30° (B)35° (C)60° (D)75°
[提示]列不等式求解.
[答案]C.
∵ 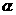 、
、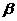 都是钝角,
都是钝角,
∴ 180°<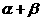 <360°.
<360°.
∴ 36°<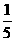
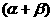 <72°.
<72°.
∵ 30°、35°、75°都不在此等圆内,仅60°属此等圆.
∴ 选C.
20.如图,∠AOB=∠BOC=∠COD=∠DOE=30°.图中互补的角有……( )

(A)10对 (B)4对 (C)3对 (D)4对
[提示]两个角的和为180°,这两个角叫互为补角.补角的概念仅与角的大小有关而与角的位置无关.
[答案]B.
原因如下:
∵ ∠AOB=∠BOC=∠COD=∠DOE=30°
∴ ∠AOE+∠AOC=120°+60°=180°,
∠AOE+∠BOD=120°+60°=180°,
∠AOE+∠COE=120°+60°=180°,
∠AOD+∠BOE=90°+90°=180°.
∴ ∠AOE 与∠AOC、∠AOE 与∠BOD、∠AOE 与∠COE、∠AOD 与∠BOE 是4对互补的角.
21.∠1、∠2互为补角,且∠1>∠2,则∠2的余角是…………………………( )
(A)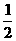
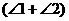 (B)
(B)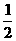 ∠1 (C)
∠1 (C)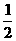
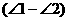 (D)
(D)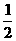 ∠2
∠2
[提示]将已知条件反映到图形上,运用数形结合的方法观察图形,便知结果,或根据互补、互余的定义进行推理.
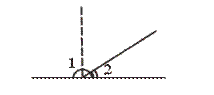
[答案]C.
由图可知:
∠2的余角
=∠1-90°
=∠1-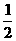
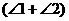
=∠1-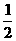 ∠1-
∠1-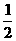 ∠2
∠2
=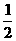
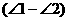 .
.
或:
∵ ∠1、∠2互为补角,
∴ ∠1+∠2=180°.
∴ ∠2的余角
=90°-∠2
=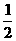
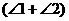 -∠2
-∠2
=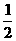 ∠1+
∠1+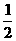 ∠2-∠2
∠2-∠2
=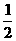
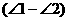 .
.
故选C.
22.设时钟的时针与分针所成角是a ,则正确的说法是………………………( )
(A)九点一刻时,∠a 是平角 (B)十点五分时,∠a 是锐角
(C)十一点十分时,∠a 是钝角 (D)十二点一刻时,∠a 是直角
[提示]时钟的时针1小时转30°,1分转0.5°;分针1小时转360°,1分转6°,还可画图,以形助思.
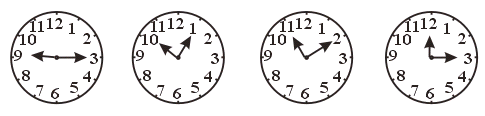
[答案]B.
7.如图,图中有________条直线,有________条射线,有________条线段,以E为顶点的角有________个.
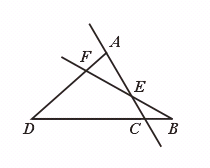
[提示]直线没有端点,可向两方无限延伸.射线有一个端点,可向一方无限延伸,线段有两个端点,不延伸.直线上一点将一条直线分成两条射线.直线上两点和它们之间的部分是线段.
[答案]1,9,12,4.
12条线段分别是:线段AF、AD、FD、DC、DB、CB、BE、BF、EF、CE、CA、EA.
8.如图,点C、D在线段AB 上.AC=6 cm,CD=4 cm,AB=12 cm,则图中所有线段的和是________cm.
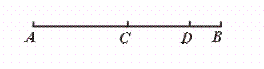
[提示]1.数出图中所有的线段;2.算出不同线段的长度;3.将所有线段的长度相加,得和.
[答案]40.
9.线段AB=12.6 cm,点C 在BA 的延长线上,AC=3.6 cm,M 是BC 中点,则AM 的长是________cm.
[提示]画出符合题意的图形,以形助思.

[答案]4.5.
∵ BC=AB+AC,M是BC中点,
∴ AM=CM-AC
=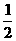 BC-AC
BC-AC
=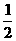 (AB+AC)-AC
(AB+AC)-AC
=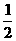 (AB-AC)
(AB-AC)
=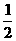 (12.6-3.6)
(12.6-3.6)
=4.5(cm).
[点评]在进行线段长度计算时,可是对其表达式进行变形、最后将值代入,求出结果.这样可简化计算,提高正确率.
10.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=________°.
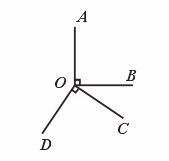
[提示]∠BOC=360°-∠AOB -∠AOD -∠DOC.
[答案]34.
11.如图,OB 平分∠AOC.且∠2∶∠3∶∠4=3∶5∶4,则∠2=________°,
∠3=________°,∠4=________°.

[提示]1周角=360°.设1份为x°,列方程求解.
[答案]72;120;96.
12.∠A与∠B互补,∠A与∠C互余,则2∠B-2∠C=________°.
[提示]∠A+∠B=180°.∠A+∠C=90°.代入要求的式子,化简即得.
[答案]180°.
∵ ∠A+∠B=180°,∠A+∠C=90°,
∴ ∠B=180°-∠A.
∴ 2∠B-2∠C=2(180°-∠A)-2∠C
=360°-2∠A-2∠C
=360°-2(∠A+∠C)
=360°-2×90°
=180°.
[点评]由已知可得关于∠A、∠B、∠C的方程组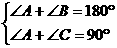 ,此时不能确定
,此时不能确定
∠B、∠C的大小,但只要将两式的两边分别相减,使得∠B-∠C=90°,2∠B-2∠C便不难求得.这种整体代入的思想是求值题中常用的方法.
13.已知:∠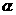 的余角是52°38′15″,则∠
的余角是52°38′15″,则∠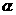 的补角是________.
的补角是________.
[提示]分步求解:先求出∠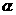 的度数,再求∠
的度数,再求∠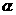 的补角的度数.
的补角的度数.
[答案]142°38′15″.
∵ ∠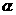 的余角是52°38′15″,
的余角是52°38′15″,
∴ ∠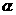 =90°-52°38′15″
=90°-52°38′15″
=89°59′60″-52°38′15″
=37°21′45″.
∴ ∠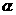 的补角=180°-37°21′45″
的补角=180°-37°21′45″
=179°59′60″-37°21′45″
=142°38′15″.
[点评]题中∠a 只起过渡作用,可考虑到而不求,作整体代入.
∵ ∠a = 90°-52°38′15″,
∴ ∠a 的补角=180°-∠a
=180°-(90°-52°38′15″)
=90°+52°38′15″
=142°38′15″.
这样避开了单位换算,利于提高运算速度及正确率.
若将已知条件反映到如图所示的图形上,运用数形结合的思想观察图形,则一目了然.一般地,已知∠a 的余角,求∠a 的补角,则∠a 的补角=90°+∠a 的余角,即任一锐角的补角比它的余角大90°.利用这个结论解该题就更准确、快捷.

14.由2点30分到2点55分,时钟的时针旋转了________度,分针旋转了________度,此刻时针与分针的夹角是________度.
[提示]分针1小时旋转360°,1分旋转6°,时钟1小时旋转30°,1分旋转0.5°.
[答案]12.5,150,117.5.
18、(2007浙江金华)水果种植大户小方,为了吸引更多的顾客,组织了观光采摘游活动.每一位来采摘水果的顾客都有一次抽奖机会:在一只不透明的盒子里有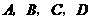 四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
四张外形完全相同的卡片,抽奖时先随机抽出一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图(或列表)的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?

解:(1)方法一:列表得
|
|
A |
B |
C |
D |
 A A |
|
(A,B) |
(A,C) |
(A,D) |
|
B |
(B,A) |
|
(B,C) |
(B,D) |
|
C |
(C,A) |
(C,B) |
|
(C,D) |
|
D |
(D,A) |
(D,B) |
(D,C) |
|
方法二:画树状图
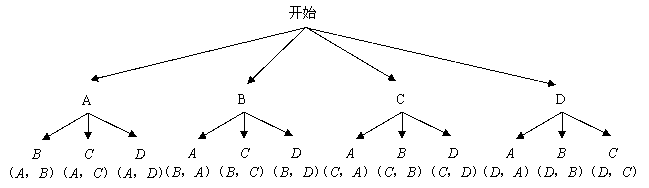

(2)获奖励的概率: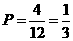 .
.
17、(2007浙江温州)一只箱子里共有3个球,其中2个白球,1个红球,它们除颜色外均相同。
(1)从箱子中任意摸出一个球是白球的概率是多少?
 (2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
(2)从箱子中任意摸出一个球,不将它放回箱子,搅匀后再摸出一个球,求两次摸出球的都是白球的概率,并画出树状图。
解:(1)从箱子中任意摸出一个球是白球的概率是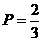
(2)记两个白球分别为白1与白2,画树状图如右所示:
从树状图可看出:事件发生的所有可能的结果总数为6,
两次摸出球的都是白球的结果总数为2,因此其概率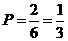 .
.
16、(2007四川成都)小华与小丽设计了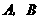 两种游戏:
两种游戏:
游戏 的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
的规则:用3张数字分别是2,3,4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再原样放回,洗匀后再第二次随机抽出一张牌记下数字.若抽出的两张牌上的数字之和为偶数,则小华获胜;若两数字之和为奇数,则小丽获胜.
游戏 的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
的规则:用4张数字分别是5,6,8,8的扑克牌,将牌洗匀后背面朝上放置在桌面上,小华先随机抽出一张牌,抽出的牌不放回,小丽从剩下的牌中再随机抽出一张牌.若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大,则小华获胜;否则小丽获胜.
请你帮小丽选择其中一种游戏,使她获胜的可能性较大,并说明理由.
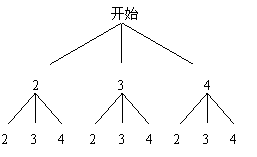
解:对游戏A:
画树状图
或用列表法
 |
2 |
3 |
4 |
|
2 |
 |
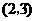 |
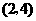 |
|
3 |
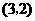 |
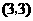 |
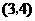 |
|
4 |
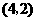 |
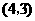 |
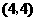 |
所有可能出现的结果共有9种,其中两数字之和为偶数的有5种,所以游戏 小华获胜的概率为
小华获胜的概率为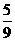 ,而小丽获胜的概率为
,而小丽获胜的概率为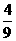 .即游戏
.即游戏 对小华有利,获胜的可能性大于小丽.
对小华有利,获胜的可能性大于小丽.
对游戏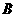 :
:
画树状图

或用列表法
 |
5 |
6 |
8 |
8 |
|
5 |
 |
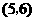 |
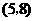 |
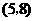 |
|
6 |
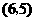 |
 |
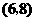 |
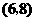 |
|
8 |
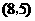 |
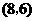 |
 |
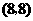 |
|
8 |
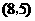 |
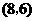 |
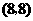 |
 |
所有可能出现的结果共有12种,其中小华抽出的牌面上的数字比小丽大的有5种;根据游戏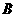 的规则,当小丽抽出的牌面上的数字与小华抽到的数字相同或比小华抽到的数字小时,则小丽获胜.所以游戏
的规则,当小丽抽出的牌面上的数字与小华抽到的数字相同或比小华抽到的数字小时,则小丽获胜.所以游戏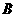 小华获胜的概率为
小华获胜的概率为 ,而小丽获胜的概率为
,而小丽获胜的概率为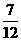 .即游戏
.即游戏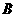 对小丽有利,获胜的可能性大于小华.
对小丽有利,获胜的可能性大于小华.
15、(2007江苏连云港)九年级1班将竞选出正、副班长各1名,现有甲、乙两位男生和丙、丁两位女生参加竞选.
(1)男生当选班长的概率是 ;
(2)请用列表或画树状图的方法求出两位女生同时当选正、副班长的概率.
解:(1)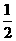 ;······································································································· 4分
;······································································································· 4分
(2)树状图为;
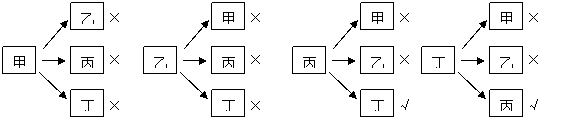

······························································································································ 8分
所以,两位女生同时当选正、副班长的概率是 .(列表方法求解略)·
.(列表方法求解略)·
·············································································································· 10分
14、(2007潜江江汉油田)亲爱的同学,下面我们来做一个猜颜色的游戏:一个不透明的小盒中,装有A、B、C三张除颜色以外完全相同的卡片,卡片A两面均为红,卡片B两面均为绿,卡片C一面为红,一面为绿.
(1)从小盒中任意抽出一张卡片放到桌面上,朝上一面恰好是绿色,请你猜猜,抽出哪张卡片的概率为0?
(2)若要你猜(1)中抽出的卡片朝下一面是什么颜色,猜哪种颜色正确率可能高一些?请你列出表格,用概率的知识予以说明.
解:(1)依题意可知:抽出卡片 的概率为0;…………………(3分)
的概率为0;…………………(3分)
|
朝上 |
B(绿 1) |
B(绿 2) |
C(绿 ) |
|
朝下 |
B(绿 2) |
B(绿 1) |
C(红 ) |
(2)由(1)知,一定不会抽出卡片 ,只会抽出卡片
,只会抽出卡片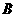 或
或 ,且抽出的卡片朝上的一面是绿色,那么可列下表:
,且抽出的卡片朝上的一面是绿色,那么可列下表:
………………………………(6分)
可见朝下一面的颜色有绿、绿、红三种可能,即:P(绿)=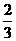 ,P(红)=
,P(红)=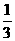 ,
,
所以猜绿色正确率可能高一些.
13、(2007贵州贵阳)小颖和小红两位同学在学习“概率”时,做投掷骰子(质地均匀的正方体)实验,他们共做了60次实验,实验的结果如下:
|
朝上的点数 |
1 |
2 |
3 |
4 |
5 |
6 |
|
出现的次数 |
7 |
9 |
6 |
8 |
20 |
10 |
(1)计算“3点朝上”的频率和“5点朝上”的频率.(4分)
(2)小颖说:“根据实验,一次实验中出现5点朝上的概率最大”;小红说:“如果投掷600次,那么出现6点朝上的次数正好是100次.”小颖和小红的说法正确吗?为什么?(4分)
(3)小颖和小红各投掷一枚骰子,用列表或画树状图的方法求出两枚骰子朝上的点数之和为3的倍数的概率.(4分)
解:(1)“3点朝上”出现的频率是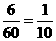 ······························································ 2分
······························································ 2分
“5点朝上”出现的频率是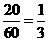 ················································································ 4分
················································································ 4分
(2)小颖的说法是错误的.这是因为,“5点朝上”的频率最大并不能说明“5点朝上”这一事件发生的频率最大.只有当实验的次数足够大时,该事件发生的频率稳定在事件发生的概率附近.························· 2分
小红的判断是错误的,因为事件发生具有随机性,故“6点朝上”的次数不一定是100次.
·················································································································· 4分
(3)列表如下:
 |
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
6 |
7 |
8 |
9 |
10 |
11 |
12 |
············································································· 2分
 ·················································································· 4分
·················································································· 4分
12、(2007广东韶关)不透明的口袋里装有红、黄、蓝三种颜色的小球若干个(除颜色外其余都相同),其中红球2个(分别标有1号、2号),篮球1个。若从中任意摸出一个球,它是篮球的概率为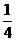 .
.
(1)求袋中黄球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用画树状图或列表格的方法,求两次摸到不同颜色球的概率.
解:(1)袋中黄球的个数为1个;····························2分
(2)方法一、列表如下:····························6分
|
* |
红1 |
红2 |
黄 |
蓝 |
|
红1 |
* |
(红1,红2) |
(红1,黄) |
(红1,蓝) |
|
红2 |
(红2,红1) |
* |
(红2,黄) |
(红2,蓝) |
|
黄 |
(黄,红1) |
(黄,红2) |
* |
(黄,蓝) |
|
蓝 |
(蓝,红1) |
(蓝,红2) |
(蓝,黄) |
* |
所以两次摸到不同颜色球的概率为: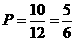 . ··························8分
. ··························8分
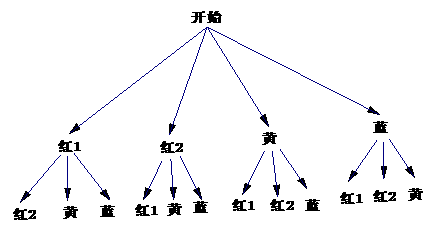 方法二,画树状图如下:
方法二,画树状图如下:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com