
题目列表(包括答案和解析)
7.已知 为矩形
为矩形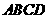 的对角线,则图中
的对角线,则图中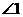 与
与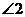 一定不相等的是( )
一定不相等的是( )

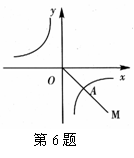
6.如图,第四象限的角平分线OM与反比例函数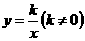
的图象交于点A,已知OA=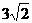 ,则该函数的解析式为( )
,则该函数的解析式为( )
A.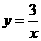 B.
B.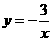 C.
C.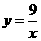 D.
D.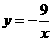
5.在平面直角坐标系中,点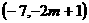 在第三象限,则m的取值范围是( )
在第三象限,则m的取值范围是( )
 A.
A.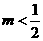 B.
B.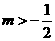 C.
C.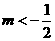 D.
D.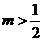
4、 把不等式组
把不等式组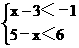 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
3.如果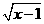 有意义,那么字母
有意义,那么字母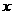 的取值范围是( )
的取值范围是( )
A.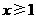 B.
B.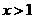 C.
C.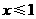 D.
D.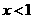
2.化简a2·a4的结果是( )
A.a8 B.a6 C.a4 D.a2
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
|
1、零上13℃记作+13℃,零下2℃可记作( )
A.2 B.-2 C. 2℃ D.-2℃
28.(本小题12分)九(1)班数学兴趣小组在社会实践活动中,进行了如下的课题研究:用一定长度的铝合金材料,将它设计成外观为长方形的三种框架,使长方形框架面积最大.
小组讨论后,同学们做了以下三种试验:
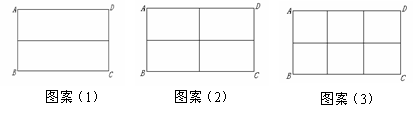
请根据以上图案回答下列问题:
(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6m,当AB为1m,长方形框架ABCD的面积是 m2;
(2)在图案(2)中,如果铝合金材料总长度为6m,设AB为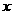 m,长方形框架ABCD的面积为S=
(用含
m,长方形框架ABCD的面积为S=
(用含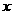 的代数式表示);当AB=
m时, 长方形框架ABCD的面积S最大;
的代数式表示);当AB=
m时, 长方形框架ABCD的面积S最大;
在图案(3)中,如果铝合金材料总长度为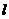 m,设AB为
m,设AB为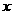 m,当AB=________m时,长方形框架ABCD的面积S最大.
m,当AB=________m时,长方形框架ABCD的面积S最大.
(3)经过这三种情形的试验,他们发现对于图案(4)这样的情形也存在着一定的规律.
探索:如图案(4),
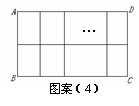 如果铝合金材料总长度为
如果铝合金材料总长度为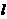 m共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.
m共有n条竖档时,那么当竖档AB多少时,长方形框架ABCD的面积最大.
26.(本小题10分)已知:抛物线C1: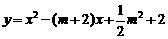 与C2:
与C2: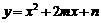 具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
具有下列特征:①都与x轴有交点;②与y轴相交于同一点.
(1)求m,n的值;
(2)试写出x为何值时,y1 >y2?
(3)试描述抛物线C1通过怎样的变换得到抛物线C2.
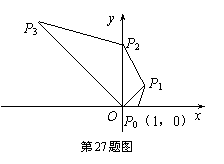
27(本小题12分)如图,在直角坐标系中,已知点P0的坐标为(1,0),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数)
(1)求点P6的坐标;
(2)求△P5OP6的面积;
(3)我们规定:把点Pn(xn,yn)(n=10,1,2,3,…)的横坐标xn、纵坐标yn都取绝对值后得到的新坐标(|xn|,| yn|)称之为点Pn的“绝对坐标”.根据图中点Pn的分布规律,请你猜想点Pn的“绝对坐标”,并写出来.
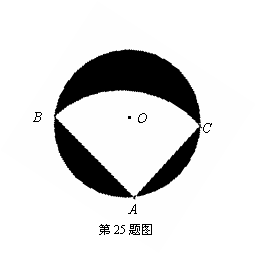
25.(本小题10分)有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
(1)求被剪掉阴影部分的面积;
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com