
题目列表(包括答案和解析)
4. 下列图形是几家通讯公司的标志,其中既是轴对称图形又是中心对称图形的是( )




|
|
|
|
3. 若反比例函数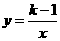 的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )
的图象在其每个象限内,y随x的增大而减小,则k的值可以是( )
A.-1 B.3 C.0 D.-3
2. 随着电子制造技术的不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7(毫米2),这个数用科学记数法表示为( )
A.7×10-6 B. 0.7×10-6 C. 7×10-7 D. 70×10-8
1.-2009的倒数是( )
A.2009 B.-2009 C.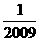 D.
D.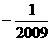
25. (本题8分)
 (1)证明:如图1,在正方形ABCD中,
(1)证明:如图1,在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,
∴△CBE≌△CDF.
∴CE=CF.………………………………………….3分
(2)GE=BE+GD成立.
理由是:
∵△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD
即∠ECF=∠BCD=90°,
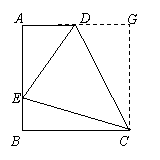 又∠GCE=45°,
又∠GCE=45°,
∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC,
∴△ECG≌△FCG. ………………………………..4分
∴GE=GF.
∴GE=DF+GD=BE+GD. ……………………..5分
(3)解:过C作CG⊥AD,交AD延长线于G.
在直角梯形ABCD中,
∵AD∥BC,
∴∠A=∠B=90°.
又∠CGA=90°,AB=BC, 图2
∴四边形ABCG 为正方形. …………………………….……………………………6分
∴AG=BC=12.
已知∠DCE=45°,
根据(1)(2)可知,ED=BE+DG.………………………………………………….. 7分
设DE=x,则DG=x-4,
∴AD=AG-DG=12-(x-4)=16-x.
在Rt△AED中,
∵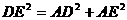 ,
,
即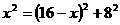 .
.
解这个方程,得:x=10.
∴DE=10.……………………………………………………………………………….8分
24.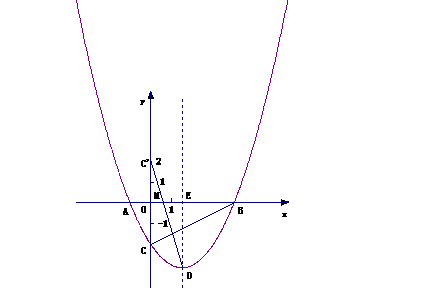 (本题7分)
(本题7分)
解:(1) 点
点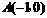 在抛物线
在抛物线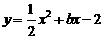 上,
上,
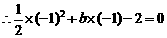 ,
,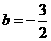 .
.
 抛物线的解析式为
抛物线的解析式为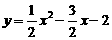 .……2分
.……2分
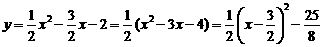 ,
,
∴顶点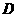 的坐标为
的坐标为 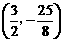 .………………3分
.………………3分
(2)当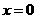 时,
时,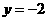 ,
,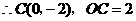 .
.
当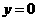 时,
时,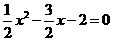 ,
,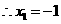 ,
,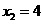 ,
,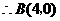 .……………………4分
.……………………4分
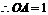 ,
,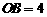 ,
,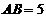 .
.
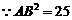 ,
,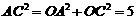 ,
,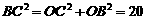 ,
,
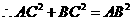 .
. 是直角三角形.………………………………………….5分
是直角三角形.………………………………………….5分
(3)作出点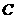 关于
关于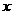 轴的对称点
轴的对称点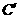 ,则
,则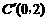 ,
,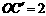 .
.
连接 交
交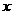 轴于点
轴于点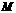 ,
,
根据轴对称性及两点之间线段最短可知,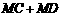 的值最小.……………………….6分
的值最小.……………………….6分
解法一:设抛物线的对称轴交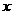 轴于点
轴于点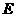 .
.
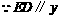 轴,
轴,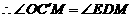 ,
,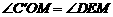 .
.
∴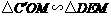 .
.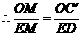 .
.
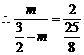 .
.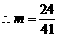 .……………………………………………………………….7分
.……………………………………………………………….7分
解法二:设直线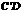 的解析式为
的解析式为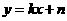 ,
,
则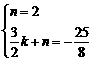 ,解得
,解得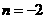 ,
,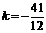 .
. 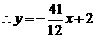 .
.
 当
当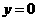 时,
时,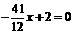 ,
,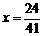 .
.
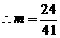 .
………………………………………………………………………………..7分
.
………………………………………………………………………………..7分
23. (本题7分)
解:(1)由题意可知,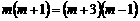 .解,得 m=3.…………………2分
.解,得 m=3.…………………2分
 ∴ A(3,4),B(6,2);
∴ A(3,4),B(6,2);
∴ k=4×3=12. …………………………………3分
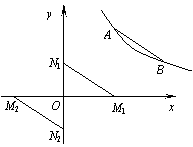
(2)存在两种情况,如图:
解法一: ①当M点在x轴的正半轴上,N点在y轴的正半
轴上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵ 四边形AN1M1B为平行四边形,
∴ 线段N1M1可看作由线段AB向左平移3个单位,再向
下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴ N1点坐标为(0,4-2),即N1(0,2);
M1点坐标为(6-3,0),即M1(3,0). ……………………………………..…4分
设直线M1N1的函数表达式为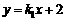 ,
,
把x=3,y=0代入,解得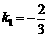 .
.
∴ 直线M1N1的函数表达式为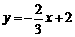 . …..……………………………………5分
. …..……………………………………5分
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵ AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴ N1M1∥M2N2,N1M1=M2N2.
∴四边形N1 M2 N2M1为平行四边形.
∴ 点M1 、M2与线段N1、 N2关于原点O成中心对称.
∴ M2点坐标为(-3,0),N2点坐标为(0,-2).……………………………………6分
设直线M2N2的函数表达式为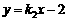 ,
,
把x=-3,y=0代入,解得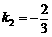 ,∴ 直线M2N2的函数表达式为
,∴ 直线M2N2的函数表达式为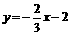 .
.
所以,直线MN的函数表达式为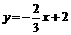 或
或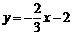 . ………………………7分
. ………………………7分
解法二 :(2)存在两种情况,如图: ①当M点在x轴的正半轴上(M1),N点在y轴的
正半轴上(N1)时,由(1)知A点坐标为(3,4),B点坐标为(6,2)
得直线AB: 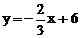 , ……………………………………………………………4分
, ……………………………………………………………4分
∵ 四边形AN1M1B为平行四边形,∴
线段N1M1可看作由直线AB向左平移3个单位得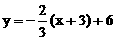 ,再向下平移2个单位得到
,再向下平移2个单位得到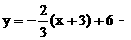 2,
2,
化简得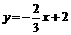 (也可看作向下平移2个单位得
(也可看作向下平移2个单位得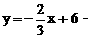 2,再向左平移3个单位得到
2,再向左平移3个单位得到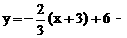 2化简得
2化简得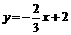 )……………………………………..5分
)……………………………………..5分
② 同解法一.
22. (本题4分)
画图正确 给4分.
,
21. (本题5分)
解法(一):如图,过点C作 AB边上的高CE. ………………………1分
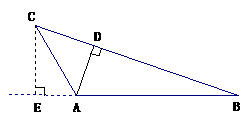 则∠CAE = 180°-120° = 60°.
则∠CAE = 180°-120° = 60°.
在Rt△ACE中,∠CEA= 90°,
∵sin∠CAE =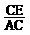 ,cos∠CAE=
,cos∠CAE=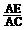 ,
,
∴CE=AC·sin60°=2×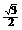 =
=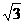 ,
,
AE=AC·cos60°=2×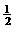 =1.
=1.
∴BE=AB+AE= 5. ……………………………………………………3分
在Rt△CBE中,由勾股定理,得,BC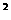 =CE
=CE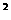 +BE
+BE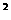 =3+25 =28.
=3+25 =28.
∴BC = 2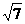 …………………………………………………………….4分
…………………………………………………………….4分
∵AD⊥BC,
∴sin∠B =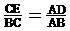 .
.
∴AD=  5分
5分
解法二:同解法一,得BC = 2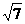 …………………………………..4分
…………………………………..4分
 ∵
∵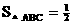 BC·AD=
BC·AD=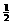 AB·CE
AB·CE
|
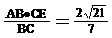
20. (本题6分)
(本题6分)
(1)调查的学生数为: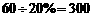 ...2分
...2分
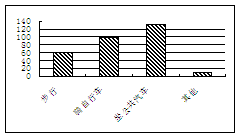
(2)如下表 ………………… 5分
(3)如右图 ……………………6分
|
步行 |
骑自行车 |
坐公共汽车 |
其 他 |
|
|
99 |
132 |
9 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com