
题目列表(包括答案和解析)
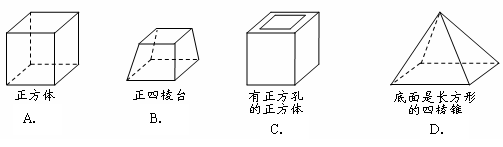
4. 在下面的四个几何体中,它们各自的左视图与主视图不全等的是
3. 若∠α=50°,则∠α的补角等于
A.150° B.130° C.50° D.40°
2. 在一场“世界金融风暴”中,我国为了防止经济下滑,2008年11月国务院出台4万亿元经济刺激方案.将4万亿元用科学记数法表示为
A.4×108元 B.4×1010元 C.4×1012元 D.4×1014元
1. 计算-1×2的结果是
A.1 B.2 C.-3 D.-2
14.知:半径不等的⊙O1与⊙O2相切于点P,直线AB、CD都经过点P,并且AB分别交⊙O1、⊙O2于A、B两点,CD分别交⊙O1、⊙O2于C、D两点(点A、B、C、D、P互不重合),连结AC和BD.
(1)请根据题意画出图形;
(2)根据你所画的图形,写出一个与题设有关的正确结论,并证明这个结论(结论中不能出现题设以外的其他字母).
13.某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形;
乙同学:我发现边数是6时,它也不一定是正多边形.
如图8,△ABC是正三角形,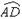 =
=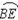 =
=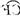 ,可以证明六边形ADBECF的各内角相等,但它未必是正六边形;
,可以证明六边形ADBECF的各内角相等,但它未必是正六边形;
丙同学:我能证明,边数是5时,它是正多边形.我想,边数是7时,它可能也是正多边形.
……
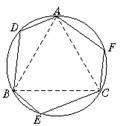
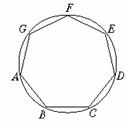
图8 图9
(1)请你说明乙同学构造的六边形各内角相等.
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图9)是正七边形(不必写已知、求证).
(3)根据以上探索过程,提出你的猜想(不必证明).
12.如图7,⊙O表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到的扇形面中的一个再等分成4个扇形;以后按第2次剪裁的作法进行下去.
(1)请你在⊙O中,用尺规作出第2次剪裁后得到的7个扇形(保留痕迹,不写作法).
(2)请你通过操作和猜想,将第3、第4和第n次裁剪后所得扇形的总个数(S)填入下表.
|
等分圆及扇形面的次数(n) |
1 |
2 |
3 |
4 |
… |
n |
|
所得扇形的总个数(S) |
4 |
7 |
|
|
… |
|
(3)请你推断,能不能按上述操作过程,将原来的圆形纸板剪成33个扇形?为什么?
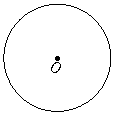
图7
11.在△ABC中,D为BC边的中点,E为AC边上的任意一点,BE交AD于点O.某学生在研究这一问题时,发现了如下的事实:
(1)当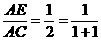 时,有
时,有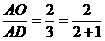 (如图3);
(如图3);
(2)当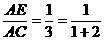 时,有
时,有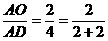 (如图4);
(如图4);
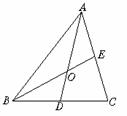
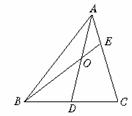
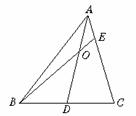
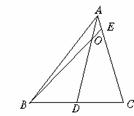
图3 图4 图5 图6
(3)当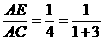 时,有
时,有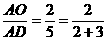 (如图5);
(如图5);
在图6中,当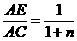 时,参照上述研究结论,请你猜想用n表示
时,参照上述研究结论,请你猜想用n表示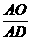 的一般结论,并给出证明(其中n是正整数).
的一般结论,并给出证明(其中n是正整数).
10.探索猜想:
(1)顺次连结等腰梯形的四条边的中点所得到的图形是什么图形?并证明你的结论.(要求画出图形,写出已知、求证和证明)
(2)如果把(1)中的“等腰梯形”换成另外的四边形,其他不变,仍得同样的结论.能得出上述结论的这类四边形具备怎样的共同特征?请把此特征写出来.(不需证明)
9.观察下列算式:
21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…
根据上述算式中的规律,你认为810的末位数字是( )
A.2 B.4 C.8 D.6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com