
题目列表(包括答案和解析)
2、给出以下四个命题:①一组对边平行的四边形是梯形;②一条对角线平分一个内角的平行四边形是菱形;③对角线互相垂直的矩形是正方形;④一组对边平行,另一组对边相等的四边形是平行四边形.其中真命题有
A.1个 B.2个 C.3个 D. 4个
[试题来源]自编
[参考答案]B
[命题意图]考察学生对于梯形、平行四边形、菱形、正方形等四边形判定的掌握情况。考题利用选择题考察面广的特点,全面考察了学生的基础知识掌握情况。
1、一次函数y=2x+3的图象沿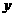 轴向下平移2个单位,那么所得图象的函数解
轴向下平移2个单位,那么所得图象的函数解
析式是 A.y=2x-3 B. y=2x+2 C. y=2x+1 D. y=2x
[试题来源]自编
[参考答案]C
[命题意图]考察学生对一次函数图象的掌握情况。教材中学习的是二次函数图象的平移, 而这里是一次函数图象的平移,此题可有效考察学生的知识迁移能力。
1、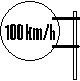 一辆轿车在某高速公路上正常行驶时的速度为
一辆轿车在某高速公路上正常行驶时的速度为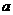
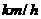 ,已知该公路对轿车的限速为100
,已知该公路对轿车的限速为100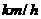 ,那么
,那么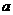 满足的不等关系应表示为( )
满足的不等关系应表示为( )
A、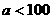 B、
B、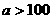 C、
C、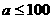 D、
D、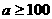
[命题意图]本题考查了学生对生活中不等式的理解、正确用不等式表示实际问题中的数量关系;讲评时主要引导学生正确理解“限时”的意义。
28.(本题共12分) 如图,矩形A’B’C’D’是矩形OABC(边OA在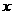 轴正半轴上,边OC在
轴正半轴上,边OC在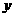 轴正半轴上)绕B点逆时针旋转得到的,O’点在
轴正半轴上)绕B点逆时针旋转得到的,O’点在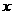 轴的正半轴上,B点的坐标为(1,3).O’C’与AB交于D点.
轴的正半轴上,B点的坐标为(1,3).O’C’与AB交于D点.
(1)如果二次函数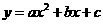 (
(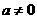 )的图象经过O,O’两点且图象顶点
)的图象经过O,O’两点且图象顶点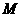 的纵坐标为
的纵坐标为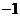 ,求这个二次函数的解析式;
,求这个二次函数的解析式;
(2)求D点的坐标.
(3)若将直线OC绕点O旋转α度(0<α<90)后与抛物线的另一个交点为点P,则以O、O’、B、P为顶点的四边形能否是平行四边形?若能,求出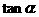 的值;若不能,请说明理由.
的值;若不能,请说明理由.
[命题意图]考查学生的对存在问题和动点问题的思考方法
及数学思想的考查。
[参考答案]28.(1)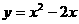 ……3 分
……3 分
(2)D(1,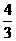 ) ……7分
) ……7分
(3)tan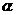 =1或
=1或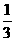 ……12分(求出一个得3分,求两个得5分)
……12分(求出一个得3分,求两个得5分)
[试题来源]网络
本资料由《七彩教育网》 提供!
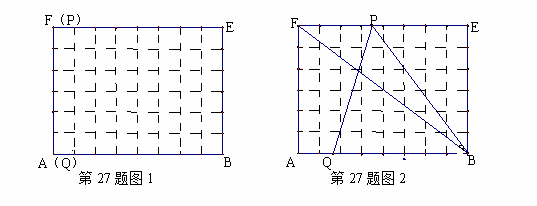
27.(本题共12分) 如图1,在6×8的网格纸中,每个小正方形的边长都为1,动点P、Q分别从点F、A出发向右移动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒1个单位,当点P运动到点E时,两个点都停止运动。
(1)请在6×8的网格纸中画出运动时间t为2秒时的线段PQ;
(2)如图2,动点P、Q在运动的过程中,PQ能否垂直于BF?请说明理由。
(3)在动点P、Q运动的过程中,△PQB能否成为等腰三角形?若能,请求出相应的运动时间t;若不能,请说明理由.
[命题意图]考查学生的数学基础知识能否灵活应用能力,及对相似三角形和三角函数的知识掌握情况。
[参考答案]27.(1)略 ……2分
(2)不能……3 分 若PQ⊥BF时,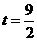 ……5分,
……5分,
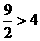 ,所以不能……6分(3)①BP=PQ,
,所以不能……6分(3)①BP=PQ,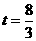 或8(舍去)…8分②BQ=PQ,
或8(舍去)…8分②BQ=PQ, 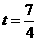 ……10分
……10分
③BP=BQ, 无解……12分
[试题来源]网络
0.3x+(60-x)≤35.5,解得35≤x≤37.所以x=35或36或37,共有包装方案3种,即简装35盒与精装25盒;简装36盒与精装24盒;简装37盒与精装23盒. ……3分 (3)由y=-10x+1440可知当x=35时,y最大=1090元.又因1090>1088,所以能用这次收入购买包装机. …………3分
[试题来源]网络
26.(本题共10分)
为了增加农民收入,村委会成立了蘑菇产销联合公司,小明家是公司成员之一,他家五月份收获干蘑菇42.5kg,干香菇35.5kg。按公司收购要求,需将两种蘑菇包装成简装和精装两种型号的盒式装蘑菇共60盒卖给公司。设包装简装型的盒数为x盒,两种型号的盒装蘑菇可获得的总利润为y(元)。包装要求及每盒获得的利润见下表:
|
品种及利润 型号型 |
装入干蘑菇重量(kg) |
装入干香菇重量(kg) |
每盒利润(元) |
|
简装型(每盒) |
0.9 |
0.3 |
14 |
|
精装型(每盒) |
0.4 |
1 |
24 |
(1)写出用含x的代数式表示y的式子;
(2)为满足公司的收购要求,问有哪几种包装方案可供选择?
(3)小明的爸爸想只用这次的收入买一台价值1088元的包装机用于扩大生产,你说能行吗?请证明你的结论.
[命题意图]考查学生的数学知识的实际应用能力,考查了不等式,一次函数的综合应用。
[参考答案]解(1)由题设易得y=14x+(60-x)×24=-10x+1440……2分
(2)依题意,有0.9x+0.4(60-x)×≤42.5 ……2分
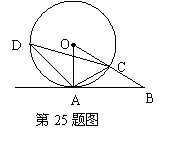
25.(本题共10分)已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=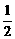 OB.
OB.
(1)试判断直线AB与⊙O的位置关系,并说明理由;
(2)若D为⊙O上一点,∠ACD=45°,AD=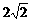 ,求扇形OAC的面积.
,求扇形OAC的面积.
 [命题意图]考查学生的数学基础掌握及灵活应用知识的能力
[命题意图]考查学生的数学基础掌握及灵活应用知识的能力
[参考答案]25﹒(1)相切(1分)理由(略)(4分)
不交待“O是半径OA的外端”扣一分(2)S=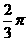
[试题来源]网络
24.(本题共10分)张红和王伟为了争取到一张观看奥运知识竞赛的入场券,他们各自设计了一个方案: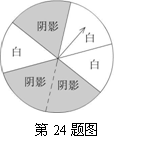 张红的方案是:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘)。
张红的方案是:转动如图所示的转盘,如果指针停在阴影区域,则张红得到入场券;如果指针停在白色区域,则王伟得到入场券(转盘被等分成6个扇形.若指针停在边界处,则重新转动转盘)。
王伟的方案是:从一副扑克牌中取出方块1、2、3,将它们背面朝上重新洗牌后,从中摸出一张,记录下牌面数字后放回,洗匀后再摸出一张.若摸出两张牌面数字之和为奇数,则张红得到入场劵;若摸出两张牌面数字之和为偶数,则王伟得到入场券.
 (1)计算张红获得入场券的概率,并说明张红的方案是否公平?
(1)计算张红获得入场券的概率,并说明张红的方案是否公平?
(2)用树状图(或列表法)列举王伟设计方案的所有情况,计算王伟
获得入场券的概率,并说明王伟的方案是否公平?
[命题意图]考查学生的数学知识的实际应用能力。
[参考答案]24﹒(1)公平……(4分)
(2)树状图或列表…(6分)王伟获奖的概率是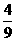 ………………………(7分)
………………………(7分)
张红获奖的概率是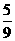 …………(8分)
…………(8分)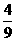 <
<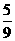 …………(9分)不公平………(10分)
…………(9分)不公平………(10分)
[试题来源]网络
23.元旦节前布置教室,同学们利用彩纸条粘成一环套一环的彩纸链,小敏测量了部分彩纸链的长度,她得到的数据如下表:
|
纸环数x(个) |
1 |
2 |
3 |
4 |
… |
|
彩纸链长度y(cm) |
20 |
35 |
50 |
65 |
… |
(1)把上表中x、y的各组对应值作为点的坐标,在如图所示的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
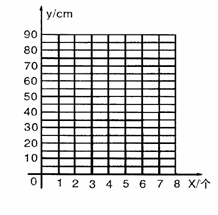 (2)教室天花板对角线长为12m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少用多少个纸环?
(2)教室天花板对角线长为12m,现需沿天花板对角线各拉一根彩纸链,则每根彩纸链至少用多少个纸环?
[命题意图]考查学生的数学知识的实际应用能力
[参考答案](1)描点 ……2分
把x=1,y=20和x=2,y=35分别代入y=kx+b中
k=15,b=5
所以y=15x+5 ……3分
(2)根据题意得 15x+5≥1200
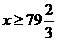 ……3分
……3分
所以至少用80个纸环.
[试题来源]网络
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com