
题目列表(包括答案和解析)
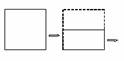
2.(·泰州市)如图,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的等腰三角形,那么剪出的等腰三角形全部展开铺平后得到的平面图形一定是


A.正三角形 B.正方形 C.正五边形
D.正六边形
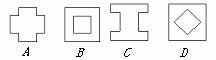
1.(•山东省)将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形. 
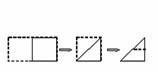

将纸片展开,得到的图形是 

8.[解析]①解决翻折类问题,首先应注意翻折前后的两个图形是全等图,找出相等的边和角.其次要注意对应点的连线被对称轴(折痕)垂直平分.结合这两个性质来解决.在运用分类讨论的方法解决问题时,关键在于正确的分类,因而应有一定的分类标准,如E为顶点、P为顶点、F为顶点.在分析题意时,也应注意一些关键的点或线段,借助这些关键点和线段来准确分类.这样才能做到不重不漏.③解决和最短之类的问题,常构建水泵站模型解决.
[答案](1) ;
;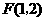 .
.
(2)在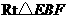 中,
中,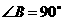 ,
,
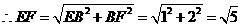 .
.
设点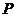 的坐标为
的坐标为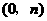 ,其中
,其中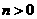 ,
,
 顶点
顶点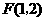 ,
,
 设抛物线解析式为
设抛物线解析式为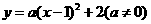 .
.
①如图①,当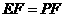 时,
时,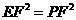 ,
,
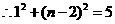 .
.
解得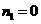 (舍去);
(舍去);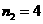 .
.
 .
.
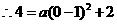 .
.
解得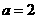 .
.
 抛物线的解析式为
抛物线的解析式为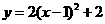
②如图②,当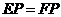 时,
时,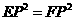 ,
,
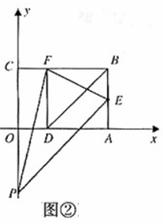
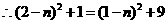 .
.
解得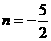 (舍去).
(舍去).
③当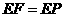 时,
时,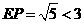 ,这种情况不存在.
,这种情况不存在.
综上所述,符合条件的抛物线解析式是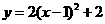 .
.
(3)存在点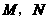 ,使得四边形
,使得四边形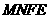 的周长最小.
的周长最小.
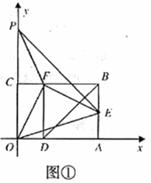
如图③,作点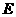 关于
关于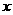 轴的对称点
轴的对称点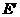 ,
,
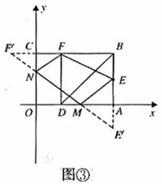
作点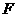 关于
关于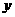 轴的对称点
轴的对称点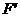 ,连接
,连接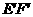 ,分别与
,分别与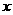 轴、
轴、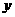 轴交于点
轴交于点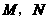 ,则点
,则点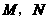 就是所求点.
就是所求点.
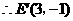 ,
,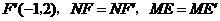 .
.
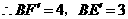 .
.
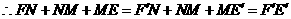
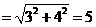 .
.
又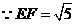 ,
,

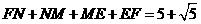 ,此时四边形
,此时四边形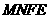 的周长最小值是
的周长最小值是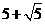 .
.
7.[解析]建立函数关系实质就是把函数y用含自变量x的代数式表示。要求线段的长,可假设线段的长,找到等量关系,列出方程求解。题中遇到“如果以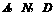 为顶点的三角形与
为顶点的三角形与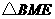 相似”,一定要注意分类讨论。
相似”,一定要注意分类讨论。
[答案](1)取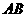 中点
中点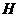 ,联结
,联结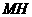 ,
,
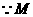 为
为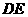 的中点,
的中点,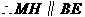 ,
,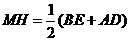 .
.
又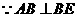 ,
,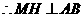 .
.
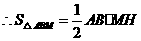 ,得
,得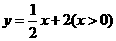 ;
;
(2)由已知得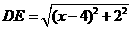 .
.
 以线段AB为直径的圆与以线段DE为直径的圆外切,
以线段AB为直径的圆与以线段DE为直径的圆外切,
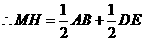 ,
,
即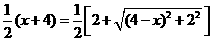 .
.
解得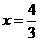 ,即线段
,即线段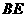 的长为
的长为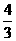 ;
;
(3)由已知,以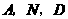 为顶点的三角形与
为顶点的三角形与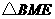 相似,
相似,
又易证得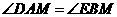 .
.
由此可知,另一对对应角相等有两种情况:①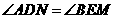 ;②
;②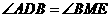 .
.
①当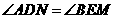 时,
时,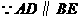 ,
,
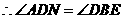 .
.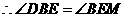 .
.
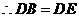 ,易得
,易得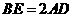 .得
.得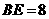 ;
;
②当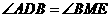 时,
时,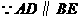 ,
,
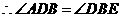 .
.
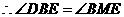 .又
.又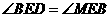 ,
,
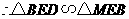 .
.
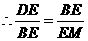 ,即
,即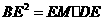 ,
,
得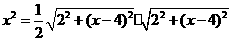 .
.
解得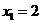 ,
,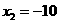 (舍去).即线段BE的长为2.
(舍去).即线段BE的长为2.
综上所述,所求线段BE的长为8或2.
6.[解析]在两圆相切的时候,可能是外切,也可能是内切,所以需要对两圆相切进行讨论.
[答案]解:(1)当0≤t≤5.5时,函数表达式为d=11-2t;
当t>5.5时,函数表达式为d=2t -11.
(2)两圆相切可分为如下四种情况:
①当两圆第一次外切,由题意,可得11-2t=1+1+t,t=3;
②当两圆第一次内切,由题意,可得11-2t=1+t-1,t=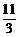 ;
;
③当两圆第二次内切,由题意,可得2t-11=1+t-1,t=11;
④当两圆第二次外切,由题意,可得2t-11=1+t+1,t=13.
所以,点A出发后3秒、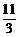 秒、11秒、13秒两圆相切.
秒、11秒、13秒两圆相切.
5.[解析]本题考察了等腰三角形的性质、垂径定理以及分类讨论思想。由AB=AC=5,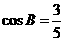 ,可得BC边上的高AD为4,圆O经过点B、C则O必在直线AD上,若O在BC上方,则AO=3,若O在BC下方,则AO=5。
,可得BC边上的高AD为4,圆O经过点B、C则O必在直线AD上,若O在BC上方,则AO=3,若O在BC下方,则AO=5。
[答案]3或5.
4.[解析]圆与斜边AB只有一个公共点有两种情况,1、圆与AB相切,此时r=2.4;2、圆与线段相交,点A在圆的内部,点B在圆的外部或在圆上,此时3<r≤4。
[答案] 3<r≤4或r=2.4
3.[解析]由折叠图形的轴对称性可知,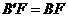 ,
,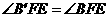 ,从而可求得B′E=BF;第(2)小题要注意分类讨论.
,从而可求得B′E=BF;第(2)小题要注意分类讨论.
[答案](1)证:由题意得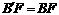 ,
,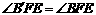 ,
,
在矩形ABCD中,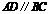 ,
,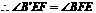 ,
,
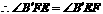 ,
,
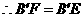 .
.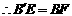 .
.
(2)答: 三者关系不唯一,有两种可能情况:
三者关系不唯一,有两种可能情况:
(ⅰ)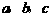 三者存在的关系是
三者存在的关系是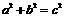 .
.
证:连结BE,则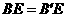 .
.
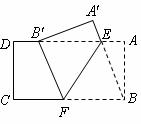
由(1)知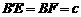 ,
,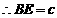 .
.
在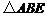 中,
中,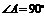 ,
, .
.
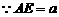 ,
,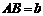 ,
,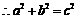 .
.
(ⅱ)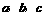 三者存在的关系是
三者存在的关系是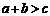 .
.
证:连结BE,则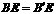 .
.
由(1)知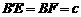 ,
,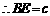 .
.
在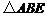 中,
中, ,
,
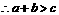 .
.
2.[解析]在没有明确腰长和底边长的情况下,要分两种情况进行讨论,当腰长是3cm,底边长是6cm时,由于3+3不能大于6所以组不成三角形;当腰长是6cm,地边长是3cm时能组成三角形.
[答案]D
1.[解析]由于已知角未指明是顶角还是底角,所以要分类讨论:(1)当50°角是顶角时,则(180°-50°)÷2=65°,所以另两角是65°、65°;(2)当50°角是底角时,则180°-50°×2=80°,所以顶角为80°。故顶角可能是50°或80°.
[答案]D .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com