
题目列表(包括答案和解析)
2. 多项式除以单项式
运算法则是:多项式除以单项式,就是用这个多项式的每一项分别除以单项式,再将所得的商相加。
例2 计算:
(1)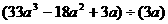
(2)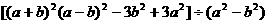
解:(1)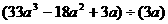
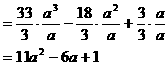
(2)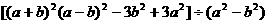
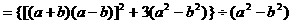

注:此题中,将被除式看作是以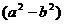 为字母的多项式。
为字母的多项式。
1. 单项式除以单项式
运算法则:将被除式,除式里的数字系数、同字母的幂分别相除,它们的积,作为商的因式,对只在被除式里含有的字母,则连同它的指数一起作为商的一个因式。
例1 计算:
(1)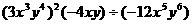
(2)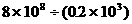
(3)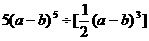
解:(1)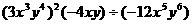
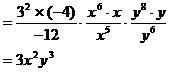
(2)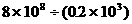
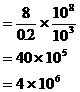
注:此题中,10被看作字母。
(3)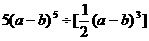
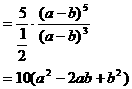
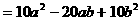
注:这里,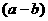 被看作一个字母。
被看作一个字母。
10.[答案](1)设能买A种笔记本x本,则能买B种笔记本(30-x)本.
依题意得: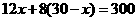 ,解得
,解得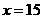 .
.
因此,能购买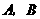 两种笔记本各15本.
两种笔记本各15本.
(2)①依题意得: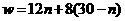 ,
,
即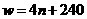 .
.
且有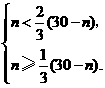 解得
解得 .
.
所以, (元)关于
(元)关于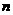 (本)的函数关系式为:
(本)的函数关系式为: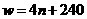 ,自变量
,自变量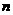 的取值范围是
的取值范围是 ,且
,且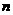 为整数.
为整数.
②对于一次函数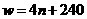 ,
,
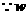 随
随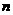 的增大而增大,且
的增大而增大,且 ,
,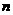 为整数,
为整数,
故当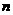 为
为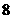 时,
时, 值最小.
值最小.
此时,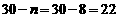 ,
,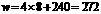 (元).
(元).
因此,当买A种笔记本8本,B种笔记本22本时,所花费用最少,为272元.
9.[答案]解:依题意,甲店B型产品有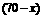 件,乙店A型有
件,乙店A型有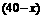 件,B型有
件,B型有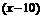 件,则
件,则
(1)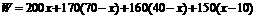
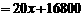 .
.
由 解得
解得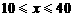 .
.
(2)由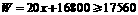 ,
,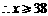 .
.
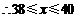 ,
,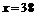 ,39,40.
,39,40.
 有三种不同的分配方案.
有三种不同的分配方案.
①x=38时,甲店A型38件,B型32件,乙店A型2件,B型28件.
②x=39时,甲店A型39件,B型31件,乙店A型1件,B型29件.
③x=40时,甲店A型40件,B型30件,乙店A型0件,B型30件.
(3)依题意:
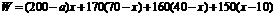
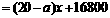 .
.
①当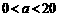 时,
时,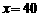 ,即甲店A型40件,B型30件,乙店A型0件,B型30件,能使总利润达到最大.
,即甲店A型40件,B型30件,乙店A型0件,B型30件,能使总利润达到最大.
②当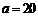 时,
时,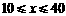 ,符合题意的各种方案,使总利润都一样.
,符合题意的各种方案,使总利润都一样.
③当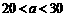 时,
时,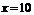 ,即甲店A型10件,B型60件,乙店A型30件,B型0件,能使总利润达到最大.
,即甲店A型10件,B型60件,乙店A型30件,B型0件,能使总利润达到最大.
8.[答案]解:(1)由从A市运往汶川x吨得:A市运往北川(500-x)吨,
B市运往汶川(400-x)吨,运往北川(x-100)吨
∴y=0.5x+0.8(500-x)+1.0(400-x)+0.4(x-100),
=0.5x+400-0.8x+400-x+0.4x-40,
=-0.9x+760
由题意得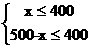
(也可由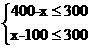 得100≤x≤400)
得100≤x≤400)
解得 100≤x≤400.
∴y=-0.9x+760(100≤x≤400)
(2)由(1)得 y=-0.9x+760.
∵-0.9<0,
∴y随x的增大而减小
又∵100≤x≤400,
∴当x=400时,y的值最小,即最小值是
y=-0.9×400+760=400(升)
这时,500-x=100,400-x=0,x-100=300.
∴总耗油量最少的最佳运输方案是从A市运往汶川400吨,北川100吨;B市的300吨全部运往北川.
此方案总耗油量是400升.
7.[答案]解:(1)设 地经杭州湾跨海大桥到宁波港的路程为
地经杭州湾跨海大桥到宁波港的路程为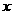 千米,
千米,
由题意得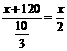 ,解得
,解得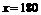 .
.
∴A地经杭州湾跨海大桥到宁波港的路程为180千米.
(2)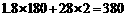 (元),
(元),
∴该车货物从 地经杭州湾跨海大桥到宁波港的运输费用为380元.
地经杭州湾跨海大桥到宁波港的运输费用为380元.
(3)设这批货物有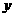 车,
车,
由题意得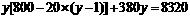 ,
,
整理得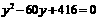 ,
,
解得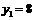 ,
,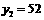 (不合题意,舍去),
(不合题意,舍去),
 这批货物有8车.
这批货物有8车.
6.[解析]解应用题的一般步骤是:审、设、列、解、验、答。正确找出题中的等量或不等关系是解题的关键。本题利用一次函数的增减性确定了总费用的最大值。
[答案](1)设这批赈灾物资运往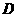 县的数量为
县的数量为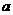 吨,运往
吨,运往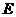 县的数量为
县的数量为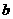 吨.
吨.
由题意,得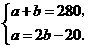 解得
解得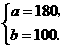
答:这批赈灾物资运往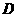 县的数量为180吨,运往
县的数量为180吨,运往 县的数量为100吨.
县的数量为100吨.
(2)由题意,得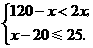
解得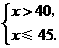 即
即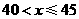 .
.
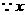 为整数,
为整数,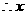 的取值为41,42,43,44,45.
的取值为41,42,43,44,45.
则这批赈灾物资的运送方案有五种.
具体的运送方案是:
方案一:A地的赈灾物资运往D县41吨,运往E县59吨;
B地的赈灾物资运往D县79吨,运往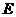 县21吨.
县21吨.
方案二:A地的赈灾物资运往D县42吨,运往E县58吨;
B地的赈灾物资运往D县78吨,运往E县22吨.
方案三:A地的赈灾物资运往D县43吨,运往E县57吨;
B地的赈灾物资运往D县77吨,运往E县23吨.
方案四:A地的赈灾物资运往D县44吨,运往E县56吨;
B地的赈灾物资运往D县76吨,运往E县24吨.
方案五:A地的赈灾物资运往D县45吨,运往E县55吨;
B地的赈灾物资运往D县75吨,运往E县25吨.
(3)设运送这批赈灾物资的总费用为 元.由题意,得
元.由题意,得
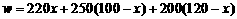
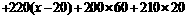
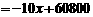 .
.
因为w随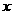 的增大而减小,且
的增大而减小,且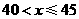 ,
,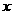 为整数.
为整数.
所以,当x=41时,w有最大值.则该公司承担运送这批赈灾物资的总费用最多为:w=60930(元).
5.[答案]解:设面值为2元的有x张,设面值为2元的有y张,依题意得
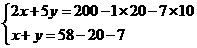
解得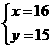
经检验,符合题意
答:面值为2元的有16张,设面值为2元的有15张.
4.[答案]解:(1)由租用甲种汽车x辆,则租用乙种汽车(8-x)辆
由题意得: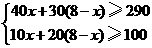
解得: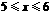
即共有2种租车方案:
第一种是租用甲种汽车5辆,乙种汽车3辆;
第二种是租用甲种汽车6辆,乙种汽车2辆.
(2)第一种租车方案的费用为 元;
元;
第二种租车方案的费用为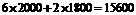 元
元
∴第一种租车方案更省费用.
3.[解析]通过表格当中的信息,我们可以利用列方程组来求出生产甲、乙两种产品的时间,然后利用列函数关系式表示出小王得到的总钱数,然后利用一次函数的增减性求出钱数的最大值.
[答案](1)解:设生产一件甲种产品需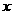 分,生产一件乙种产品需
分,生产一件乙种产品需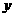 分,由题意得:
分,由题意得:
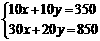 即
即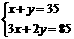
解这个方程组得: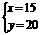
 生产一件甲产品需要15分,生产一件乙产品需要20分.
生产一件甲产品需要15分,生产一件乙产品需要20分.
(2)解:设生产甲种产品用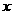 分,则生产乙种产品用
分,则生产乙种产品用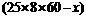 分,则生产甲种产品
分,则生产甲种产品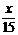 件,生产乙种产品
件,生产乙种产品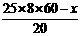 件.
件.
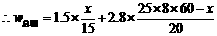
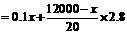

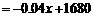
又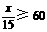 ,得
,得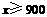
由一次函数的增减性,当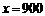 时
时 取得最大值,此时
取得最大值,此时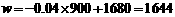 (元)
(元)
此时 甲有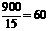 (件),
(件),
乙有: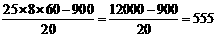 (件)
(件)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com