
题目列表(包括答案和解析)
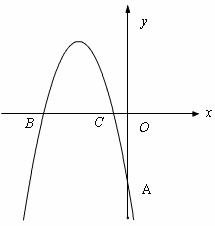
6.(·茂名)如图,在平面直角坐标系中,抛物线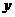 =-
=-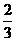
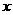
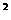 +
+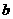
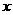 +
+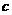 ,经过A(0,-4)、B(
,经过A(0,-4)、B(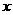
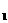 ,0)、 C(
,0)、 C(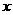
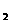 ,0)三点,且
,0)三点,且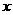
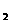 -
-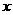
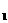 =5.
=5.
(1)求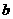 、
、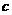 的值;
的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
5.(·恩施自治州)如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若∆ABC固定不动,∆AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.
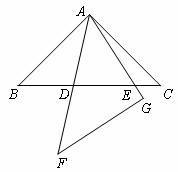

图1
(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明.
(2)求m与n的函数关系式,直接写出自变量n的取值范围.
(3)以∆ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD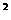 +CE
+CE =DE
=DE .
.
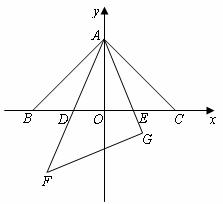

图2
(4)在旋转过程中,(3)中的等量关系BD +CE
+CE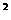 =DE
=DE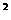 是否始终成立,若成立,请证明,若不成立,请说明理由.
是否始终成立,若成立,请证明,若不成立,请说明理由.
















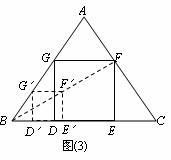
4.(·益阳) △ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
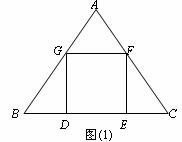

Ⅰ.证明:△BDG≌△CEF;
Ⅱ. 探究:怎样在铁片上准确地画出正方形.小聪和小明各给出了一种想法,请你在Ⅱa和Ⅱb的两个问题中选择一个你喜欢的问题解答. 如果两题都解,只以Ⅱa的解答记分.
Ⅱa. 小聪想:要画出正方形DEFG,只要能计算出
正方形的边长就能求出BD和CE的长,从而确定D点和
E点,再画正方形DEFG就容易了.
设△ABC的边长为2 ,请你帮小聪求出正方形的边长(结果用含根号的式子表示,不要求分母有理化) .
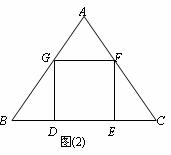

Ⅱb. 小明想:不求正方形的边长也能画出正方形. 具体作法是:
①在AB边上任取一点G’,如图作正方形G’D’E’F’;
②连结BF’并延长交AC于F;
③作FE∥F’E’交BC于E,FG∥F′G′交AB于G,
GD∥G’D’交BC于D,则四边形DEFG即为所求.
你认为小明的作法正确吗?说明理由.









类型之三 几何与代数相结合的综合题
几何与代数相结合的综合题是初中数学中涵盖广、综合性最强的题型.它可以包含初中阶段所学的代数与几何的若干知识点和各种数学思想方法,还能有机结合探索性、开放性等有关问题;它既突出考查了初中数学的主干知识,又突出了与高中衔接的重要内容,如函数、方程、不等式、三角形、四边形、相似形、圆等.它不但考查学生数学基础知识和灵活运用知识的能力还可以考查学生对数学知识迁移整合能力;既考查学生对几何与代数之间的内在联系,多角度、多层面综合运用数学知识、数学思想方法分析问题和解决问题的能力,还考查学生知识网络化、创新意识和实践能力.
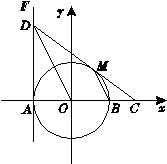
3.(·龙岩市)如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行⊙O的弦MB,连DM并延长交x轴于点C.
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求MC的长及直线DC的解析式.











2.(•沈阳市)一辆经营长途运输的货车在高速公路的A处加满油后,以每小时80千米的速度匀速行驶,前往与A处相距636千米的B地,下表记录的是货车一次加满油后油箱内余油量y(升)与行驶时间x(时)之间的关系:
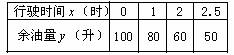

(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y与 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从A处出发行驶4.2小时到达C处,求此时油箱内余油多少升?
(3)在(2)的前提下,C处前方18千米的D处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在D处至少加多少升油,才能使货车到达B地.(货车在D处加油过程中的时间和路程忽略不计)










类型之二 几何类型的综合题
几何综合题考查知识点多、条件隐晦,要求学生有较强的理解能力,分析能力,解决问题的能力,对数学知识、数学方法有较强的驾驭能力,并有较强的创新意识与创新能力. 解决几何型综合题的关键是把代数知识与几何图形的性质以及计算与证明有机融合起来,进行分析、推理,从而达到解决问题的目的.
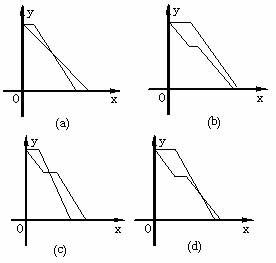
1.(·安徽省)刚回营地的两个抢险分队又接到救灾命令:一分队立即出发往30千米的A镇;二分队因疲劳可在营地休息a(0≤a≤3)小时再往A镇参加救灾。一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方地形复杂,必须由一分队用1小时打通道路,已知一分队的行进速度为5千米/时,二分队的行进速度为(4+a)千米/时。
⑴若二分队在营地不休息,问二分队几小时能赶到A镇?
⑵若二分队和一分队同时赶到A镇,二分队应在营地休息几小时?
⑶下列图象中,①②分别描述一分队和二分队离A镇的距离y(千米)和时间x(小时)的函数关系,请写出你认为所有可能合理的代号,并说明它们的实际意义。







4.[解析]我们可以先假设存在这样的抛物线,如果能够求出对应的值,则存在,如果求不出,则不存在.
[答案](1)∵ 平移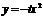 的图象得到的抛物线F的顶点为Q,
的图象得到的抛物线F的顶点为Q,
∴ 抛物线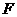 对应的解析式为:
对应的解析式为: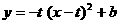 .
.
∵ 抛物线与x轴有两个交点,∴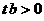 .
.
令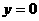 , 得
, 得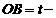
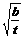 ,
,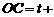
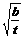 ,
,
∴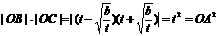
即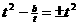 , 所以当
, 所以当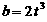 时, 存在抛物线F使得
时, 存在抛物线F使得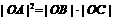 .
.
(2) ∵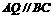 ,∴
,∴ 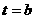 ,得F:
,得F:
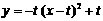 ,
,
解得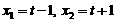
在 中,
中,
1) 当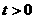 时,由
时,由 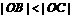 , 得
, 得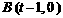 ,
,
当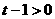 时, 由
时, 由
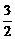
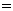
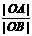
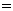
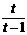 ,
,
解得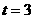 ,
,
此时, 二次函数解析式为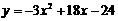 ;
;
当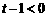 时, 由
时, 由
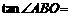
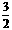 =
=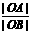 =
=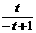 , 解得
, 解得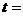
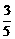 ,
,
此时,二次函数解析式为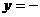
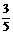
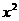 +
+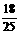
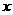 +
+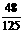 .
.
2) 当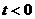 时, 由
时, 由 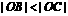 , 将
, 将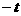 代
代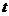 , 可得
, 可得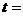
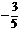 ,
, 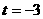 ,
,
(也可由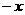 代
代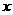 ,
,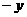 代
代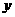 得到)
得到)
所以二次函数解析式为 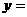
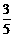
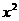 +
+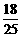
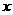 –
–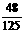 或
或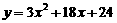 .
.
3.[解析]解决在产品的营销过程中如何获得最大利润的“每每型”试题成为近年中考的热点问题。每每型”试题的特点就是每下降,就每减少,或每增长,就每减少。解决这类问题的关键就是找到单价降低后,该商场每天的销售量。“每每型”试题都可以转化为二次函数最值问题,利用二次函数的图像和性质加以解决.
[答案](1)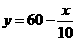
(2)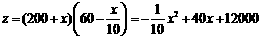
(3)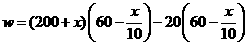
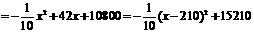
当x=210时, 有最大值.
有最大值.
此时,x+200=410,就是说,当每个房间的定价为每天410元时, 有最大值,且最大值是15210元.
有最大值,且最大值是15210元.
2.[解析]先建立函数关系式,把它转化为二次函数的一般形式,然后根据二次函数的顶点坐标公式进行求极值.
[答案]解:设增种x棵树,果园的总产量为y千克,依题意得:y=(100 + x)(40 – 0.25x ) =4000 – 25x + 40 x – 0,25x2 = - 0.25 x2 + 15x + 4000
因为a= - 0.25<0,所以当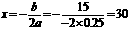 ,
,
y有最大值
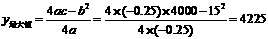
答:增种30棵枇杷树,投产后可以使果园枇杷的总产量最多,最多总产量是4225千克.
1.[解析]从函数图象容易看出前面一段是出台该项优惠政策前的情况,后面一段是出台该项优惠政策后的情况,前面一段所有的量已经知道,容易求出该果园共销售脐橙的重量,为后面一段的求值奠定了基础.
[答案]解:(1)政策出台前的脐橙售价为
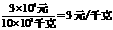 ;
;
(2)设剩余脐橙为x吨,则
103×(3×9+0.2)x=11.7×104
∴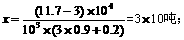
该果园共销售了10 +30 = 40吨脐橙 ;
(3)①设这个一次函数的解析式为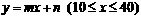 ,
,
代入两点(10,3)、(40,11.7)
得: 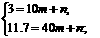
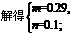 函数关系式为
函数关系式为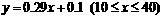 ,
,
②令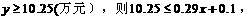
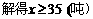
答:(1)原售价是3元/千克;(2)果园共销售40吨脐橙;(3)①函数关系式为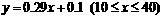 ;
;
②今年至少要销售35吨,总收入才达到去年水平.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com