
题目列表(包括答案和解析)
3.已知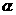 、
、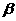 是方程
是方程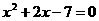 的两个实数根,求
的两个实数根,求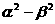 的值。
的值。
2.(吉林中考题)某初一学生在做作业时,不慎将墨水瓶打翻,使一道作业题只看到如下字样:“甲、乙两地相距40km,摩托车的速度为45km/h,运货汽车的速度为35km/h,
 ?”(涂黑部分表示被墨水覆盖的若干文字)请将这道作业题补充完整,并列方程解答。
?”(涂黑部分表示被墨水覆盖的若干文字)请将这道作业题补充完整,并列方程解答。
1.(扬州市中考压轴题)用水清洗一堆青菜上残留的农药,对用水清洗一次的效果作如下规定:用一桶水可洗掉青菜上残留农药量的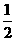 ,用水越多洗掉的农药量也越多,但总还有农药残留在青菜上。设用
,用水越多洗掉的农药量也越多,但总还有农药残留在青菜上。设用 桶水清洗一次后,青菜上残留的农药量与本次清洗前残留的农药量之比为
桶水清洗一次后,青菜上残留的农药量与本次清洗前残留的农药量之比为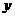 。
。
⑴试解释“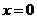 时,
时,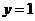 ”的实际意义;
”的实际意义;
⑵设当 取
取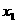 、
、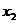 时,对应的
时,对应的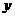 值分别为
值分别为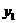 、
、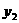 ,如果
,如果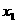 >
>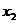 >1,试比较
>1,试比较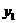 、
、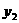 、
、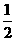 的大小关系(直接写出结论);
的大小关系(直接写出结论);
⑶设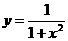 ,现有
,现有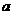 (
(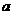 >0)桶水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后青菜上残留的农药量比较少?说明理由。
>0)桶水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后青菜上残留的农药量比较少?说明理由。
3.策略开放与探索
策略开放性问题,一般指解题方法不惟一或解题路径不明确的问题,这类问题要求解题
者不墨守成规,善于标新立异,积极发散思维,优化解题方案和过程。
[例1] (乌鲁木齐中考题)如图,已知在△ABC中,AB=AC,AD⊥BC于D,且AD=BC=4。若将此三角形沿AD剪开成为两个三角形,在平面上把这两个三角形拼成一个四边形,你能拼出所有的不同形状的四边形吗?画出所拼四边形的示意图(标出图中的直角),并分别写出所拼四边形的对角线的长(不要求写计算过程,只需写出结果)。
[解析]:经过适当拼合可以组成以下四种不同形状的四边形。
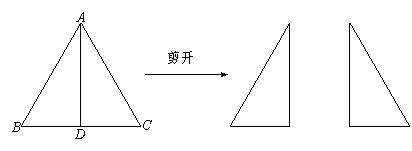
 ①矩形(如图1):
①矩形(如图1):
此时两条对角线的长相等,均为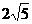 ;
;
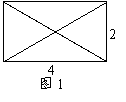
②平行四边形(如图2):
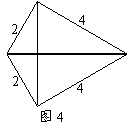 此时两条对角线的长分别为4和
此时两条对角线的长分别为4和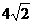 ;
;
 ③平行四边形(如图3):
③平行四边形(如图3):
此时两条对角线的长分别为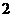 和
和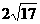 ;
;
④四边形(如图4):
此时两条对角线的长分别为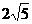 和
和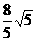 ;
;
[评注]:这是一道集开放探索、操作应用于一体的试题,既可考查学生的探索能力,又可锻炼学生的动手操作能力,是一道难得的好题。
[例2] (湖北黄冈中考题)在一服装厂里有大量形状为等腰直角三角形的边角布料。现找出其中的一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其他边相切。请设计出所有符合题意的方案示意图,并求出扇形的半径(只要求画出扇形,并直接写出扇形半径)。
[解析]:根据题意,可考虑圆心在顶点和直角边、斜边上,设计出符合题意的方案示意图。
可以设计如下图的四种方案:

[评注]:本题要求设计出符合题意的方案示意图,因此,在分类讨论时要做到不重复、不遗漏,特别是圆心在顶点上的两种情况不能遗漏,这是一道考查思维广阔性与周密性的好题。
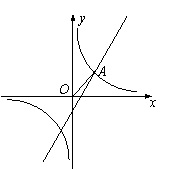 [例3] (吉林省中考题)已知反比例函数
[例3] (吉林省中考题)已知反比例函数 和一次函数
和一次函数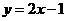 ,其中一次函数的图象经过(
,其中一次函数的图象经过(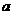 ,
,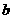 ),(
),(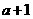 ,
,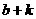 )两点。
)两点。
⑴求反比例函数的解析式;
⑵如图,已知点A在第一象限,且同时在上述两个函数
的图象上,求A点的坐标;
⑶利用⑵的结果,请问:在 轴上是否存在点P,使△AOP
轴上是否存在点P,使△AOP
为等腰三角形?若存在,把符合条件的P点坐标都求出来;若
不存在,请说明理由。
[解析]:易求⑴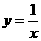 ;⑵A点的坐标为(1,1);
;⑵A点的坐标为(1,1);
⑶讨论OA为腰、为底时,得出P点的坐标。
OA=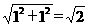 ,OA与
,OA与 轴所夹的锐角为45°。
轴所夹的锐角为45°。
①当OA为腰时,由OA=OP,得P1(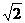 ,0),P2(
,0),P2(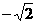 ,0);由OA=AP,得P3(2,0);
,0);由OA=AP,得P3(2,0);
②当OA为底时,得P4(1,0)。
∴这样的点有4个,分别是(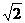 ,0),(
,0),(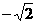 ,0),(2,0),(1,0)。
,0),(2,0),(1,0)。
[评注]:第⑶小题是一个“存在性”问题,也是一个分类讨论问题,解题的过程呈开放型,有利于考查学生的思维能力和全面思考的能力。
[例4] (苏州市中考题)已知:⊙O1与⊙O2外切于点P,过点P的直线分别交⊙O1、⊙O2于点B、A,⊙O1的切线BN交⊙O2于点M、N,AC为⊙O2的弦。
⑴如图,设弦AC交BN于点D,求证:AP·AB=AC·AD。
⑵如图,当弦AC绕点A旋转,弦AC的延长线交直线BN于点D时,试问AP·AB=
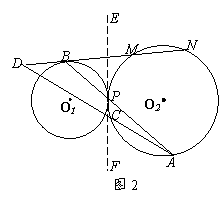 AC·AD是否仍然成立?证明你的结论。
AC·AD是否仍然成立?证明你的结论。
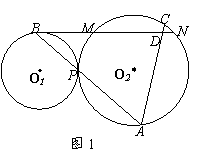
[解析]:⑴略。⑵当弦AC绕点A旋转后,若探索AP·AB=AC·AD是否仍然成立,其实是探索△APC与△ADB是否仍然相似?
⑴略;⑵仍然成立。连结PC,过点P作⊙O1和⊙O2的公切线EF,则∠MBP=∠EPB,
∴∠ABD=∠APE。∵∠ACP=∠APE, ∴∠ABD=∠ACP。
又∠A=∠A,
∴△APC∽△ADB,∴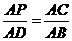 ,即AP·AB=AC·AD。
,即AP·AB=AC·AD。
[评注]:在给定条件下探索尚不明确的结论,其解法是,需要对题目的条件进行具体分析、判断,通过推理来获取结论。
[题型设计与能力训练]
13.⑴在Rt△AOB中,∵OA=3,sin∠OAB= ,
,
∴cos∠OAB=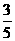 ,∴AB=5,OB=4,BP=5-3=2。
,∴AB=5,OB=4,BP=5-3=2。
在Rt△APM中,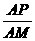 =cos∠OAB=
=cos∠OAB=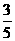 ,
,
∴AM=5,OM=2,∴点M(0,-2) 又 △NPM∽△AOB
∴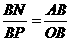 ∴
∴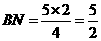
∴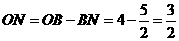 ∴点N(
∴点N(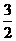 ,0)
,0)
设MP的解析式为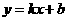 , ∵MP经过M、N两点,
, ∵MP经过M、N两点,
∴得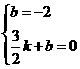 ,解之,得
,解之,得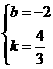
∴MP的解析式为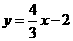 。
。
设过M、N、B的抛物线解析式为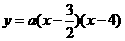 ,且点M(
,且点M( ,
,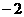 ),可得
),可得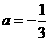 。
。
∴抛物线的解析式为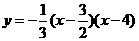 ,即
,即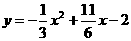 。
。
⑵①四边形OMCB是矩形。
证明:在⊙A不动、⊙B运动变化过程中,
恒有∠BAO=∠MAP,OA=OP,∠AOB=∠APM=90°,∴△AOB≌△APM。
∴OB=PM,AB=AM。∴PB=OM。而PB=BC, ∴OM=BC。
由切线长定理知 MC=MP, ∴MC=OB。∴四边形MOBC是平行四边形。
又 ∵∠MOB=90°, ∴四边形MOBC是矩形。
②存在。由上述证明可知Rt△MON≌Rt△BPN,∴BN=MN。
因此在过M、N、B三点的抛物线内有以BN为腰的等腰三角形MNB存在。
由抛物线的轴对称性可知,在抛物线上必有一点M′与M关于其对称轴对称,
∴BN=B M′。 这样得到满足条件的三角形有两个,△MNB和△M′NB。
12.解:⑴设A(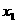 ,0)、B(
,0)、B(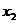 ,0),由题设可求得C点的坐标为(0,
,0),由题设可求得C点的坐标为(0,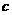 ),且
),且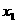 <0,
<0,
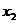 >0,∵
>0,∵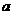 <0,∴
<0,∴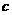 >0
>0
由S△AOC-S△BOC=OA·OB得: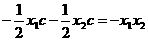
得: 得:
得: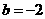
⑵设抛物线的对称轴与 轴交于点M,与△PAB的外接圆交于点N,
轴交于点M,与△PAB的外接圆交于点N,
∵tan∠CAB=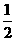 ,∴
,∴ ,∴A点的坐标为(
,∴A点的坐标为(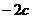 ,0)
,0)
∴A点在抛物线上, ∴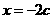 ,
,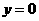 代入
代入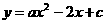 ,得
,得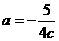
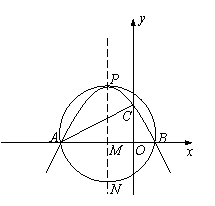 又 ∵
又 ∵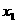 、
、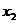 为方程
为方程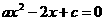 的两根,
的两根,
∴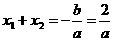 ,即:
,即: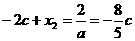
∴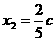 ∴B点的坐标为(
∴B点的坐标为(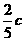 ,0),
,0),
∴顶点P的坐标为(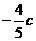 ,
,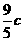 )
)
由相交弦定理得: AM·BM=PM·MN
又 ∵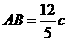 , ∴AM=BM=
, ∴AM=BM=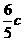 ,PM=
,PM=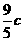
∴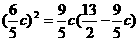 , ∴
, ∴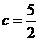 ,
,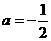
∴所求的抛物线的函数解析式是: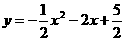
11.⑴B(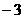 ,
, );⑵
);⑵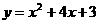 或
或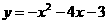 ;
;
⑶存在点P(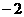 ,
,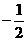 ),使△APE的周长最小。
),使△APE的周长最小。
10.⑴连结O1A,O1B,O1 O2。 ∵⊙O1与⊙O2相切于点P,∴点P在O1 O2上。
∵∠APB=90°, ∴∠2+∠4=90°。
∵∠1=∠2,∠3=∠4, ∴∠O1+∠O2=180°,O1A∥O2B。
又⊙O1与⊙O2的半径均为 ,∴四边形O1 AB
O2是平行四边形。
,∴四边形O1 AB
O2是平行四边形。
∴AB=O1 O2=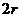 。
。
⑵连结O1A,O1 O2,O2B,同⑴可证O1A∥O2B。过点B作BC∥O1 O2,交O1A于点C。
在△ACB中,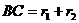 ,
, 。
。
由三角形三边关系,得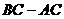 <
< <
<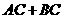 。∴
。∴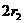 <
< <
<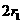 。
。
9.⑴连结BM,先证∠ECN=∠MBN,再证Rt△CEN≌Rt△BMN。
⑵连结BD、BE、AC,先证△ABE≌△ACE,再证△BED∽△FEB。
⑶结论成立,仿⑵可证之。
8.⑴延长线CG交于⊙O于H,易证△ACG∽△AFC;
⑵当点E是AD(点A除外)上任意一点时,上述结论仍成立。证略。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com