
题目列表(包括答案和解析)
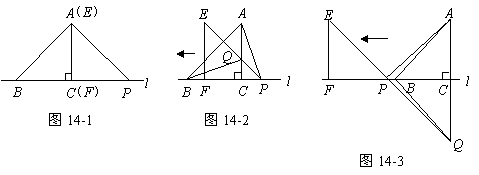
10、(08河北)如图14-1, 的边
的边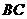 在直线
在直线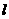 上,
上,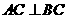 ,且
,且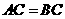 ;
;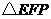 的边
的边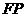 也在直线
也在直线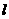 上,边
上,边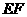 与边
与边 重合,且
重合,且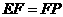 .
.
(1)在图14-1中,请你通过观察、测量,猜想并写出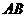 与
与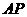 所满足的数量关系和位置关系;
所满足的数量关系和位置关系;
(2)将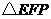 沿直线
沿直线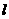 向左平移到图14-2的位置时,
向左平移到图14-2的位置时,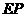 交
交 于点
于点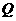 ,连结
,连结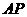 ,
,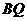 .猜想并写出
.猜想并写出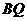 与
与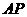 所满足的数量关系和位置关系,请证明你的猜想;
所满足的数量关系和位置关系,请证明你的猜想;
(3)将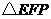 沿直线
沿直线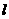 向左平移到图14-3的位置时,
向左平移到图14-3的位置时,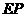 的延长线交
的延长线交 的延长线于点
的延长线于点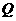 ,连结
,连结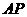 ,
,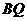 .你认为(2)中所猜想的
.你认为(2)中所猜想的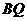 与
与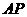 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.

27.(本题满分12分)
如图,直线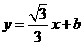 经过点B(
经过点B(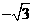 ,2),且与x轴交于点A.将抛物线
,2),且与x轴交于点A.将抛物线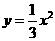 沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠BAO的度数;
(2)抛物线C与y轴交于点E,与直线AB交于两点,其中一个交点为F.
当线段EF∥x轴时,求平移后的抛物线C对应的函数关系式;
(3)在抛物线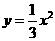 平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.
平移过程中,将△PAB沿直线AB翻折得到△DAB,点D能否落在抛物线C上?如能,求出此时抛物线C顶点P的坐标;如不能,说明理由.

18.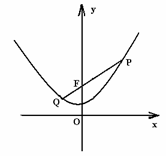 (本小题13分)如图,已知点
(本小题13分)如图,已知点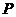 是抛物线
是抛物线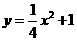 上的任意一点,
上的任意一点,
记点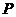 到
到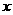 轴距离为
轴距离为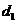 ,点
,点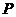 与点
与点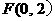 的距离为
的距离为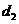
(1)证明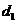 =
=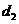 ;
;
(2)若直线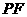 交此抛物线于另一点Q(异于
交此抛物线于另一点Q(异于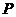 点),
点),
试判断以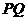 为直径的圆与
为直径的圆与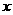 轴的位置关系,并说明理由.
轴的位置关系,并说明理由.
盐城市二○○八
27.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请售答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x函数关系式(不必写出x的取值范围);
(3)商店想在月销售成本不超过1000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
河北省2007
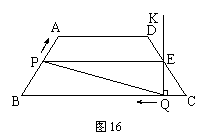
如图16,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).
(1)当点P到达终点C时,求t的值,并指出此时BQ的长;
(2)当点P运动到AD上时,t为何值能使PQ∥DC ?
(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的函数关系式;(不必写出t的取值范围)
 (4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.
(4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.
(08河北)(本小题满分12分)
如图15,在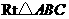 中,
中,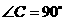 ,
,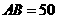 ,
,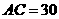 ,
,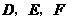 分别是
分别是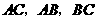 的中点.点
的中点.点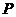 从点
从点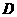 出发沿折线
出发沿折线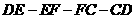 以每秒7个单位长的速度匀速运动;点
以每秒7个单位长的速度匀速运动;点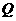 从点
从点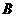 出发沿
出发沿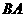 方向以每秒4个单位长的速度匀速运动,过点
方向以每秒4个单位长的速度匀速运动,过点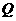 作射线
作射线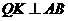 ,交折线
,交折线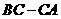 于点
于点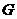 .点
.点 同时出发,当点
同时出发,当点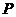 绕行一周回到点
绕行一周回到点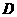 时停止运动,点
时停止运动,点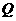 也随之停止.设点
也随之停止.设点 运动的时间是
运动的时间是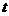 秒(
秒(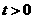 ).
).
(1)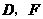 两点间的距离是
;
两点间的距离是
;
(2)射线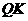 能否把四边形
能否把四边形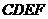 分成面积相等的两部分?若能,求出
分成面积相等的两部分?若能,求出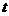 的值.若不能,说明理由;
的值.若不能,说明理由;
(3)当点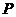 运动到折线
运动到折线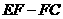 上,且点
上,且点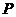 又恰好落在射线
又恰好落在射线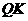 上时,求
上时,求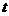 的值;
的值;
(4)连结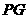 ,当
,当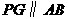 时,请直接写出
时,请直接写出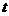 的值.
的值.

2008年湖北黄岗罗田县
27、(12分)某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元进行批量生产。已知生产每件产品的成本为40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为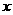 元,年销售量为
元,年销售量为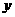 万件,年获利(年获利=年销售额-生产成本-投资)
万件,年获利(年获利=年销售额-生产成本-投资)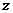 万元。
万元。
(1)试写出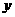 与
与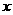 之间的函数关系式;(不必写出
之间的函数关系式;(不必写出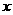 的取值范围)
的取值范围)
(2)试写出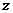 与
与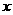 之间的函数关系式;(不必写出
之间的函数关系式;(不必写出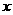 的取值范围)
的取值范围)
(3)计算销售单价为160元时的年获利,并说明同样的年获利,销售单价还可以定为多少元?相应的年销售量分别为多少万件?
(4)公司计划:在第一年按年获利最大确定的销售单价进行销售,第二年年获利不低于1130万元。请你借助函数的大致图象说明,第二年的销售单价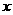 (元)应确定在什么范围内?
(元)应确定在什么范围内?
河北省2002
27.某机械租赁公司有同一型号的机械设备40套。经过一段时间的经营发现:当每套机械设备的月租金为270元时,恰好全部租出。在此基础上,当每套设备的月租金每提高10元时,这种设备就少租出一套,且没租出的一套设备每月需支出费用(维护费、管理费等)20元。设每套设备的月租金为x(元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为y(元)。
(1)用含x的代数式表示未出租的设备数(套)以及所有未出租设备(套)的支出费
(2)求y与x之间的二次函数关系式;
(3)当月租金分别为300元和350元式,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?请你简要说明理由;
(4)请把(2)中所求出的二次函数配方成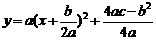 的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
的形式,并据此说明:当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益是多少?
2003年河北省
25. (本小题满分12分)
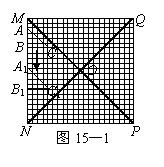 如图15-1和15-2,在20×20的等距网格(每格的宽和高均是1个单位长)中,
如图15-1和15-2,在20×20的等距网格(每格的宽和高均是1个单位长)中,
Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速
度先向下平移,当BC边与网的底部重合时,继续同样的速度向右
平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间
为x秒,△QAC的面积为y.
(1)如图15-1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,
请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图15-2,在Rt△ABC向下平移的过程中,请你求出y与
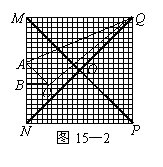 x的函数关系式,并说明当x分别取何值时,y取得最大值和
x的函数关系式,并说明当x分别取何值时,y取得最大值和
最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y
取得最大值和最小值?最大值和最值分别是多少?为什么?
(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)
2006年河北省
利达经销店为某工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7. 5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大.”你认为对吗?请说明理由.
河北省2005
25.(本小题满分12分)
一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,每款手机至少要购进8部,且恰好用完购机款61000元.设购进A型手机x部,B型手机y部.三款手机的进价和预售价如下表:
|
手机型号 |
A型 |
B型 |
C型 |
|
进 价(单位:元/部) |
900 |
1200 |
1100 |
|
预售价(单位:元/部) |
1200 |
1600 |
1300 |
(1)用含x,y的式子表示购进C型手机的部数;
(2)求出y与x之间的函数关系式;
(3)假设所购进手机全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.
①求出预估利润P(元)与x(部)的函数关系式;
(注:预估利润P=预售总额-购机款-各种费用)
②求出预估利润的最大值,并写出此时购进三款手机各多少部.
2004年河北省
25.(本题10分)如图已知二次函数图象的顶点坐标为C(1,1),直线) 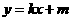 的图象与该二次函数的图象交于A、B两点,其中A点坐标为
的图象与该二次函数的图象交于A、B两点,其中A点坐标为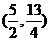 ,B点在y轴上,直线与x轴的交点为F.P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
,B点在y轴上,直线与x轴的交点为F.P为线段AB上的一个动点(点P与A、B不重合),过P作x轴的垂线与这个二次函数的图象交于E点.
(1)求k,m的值及这个二次函数的解析式;
(2)设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在点P,使
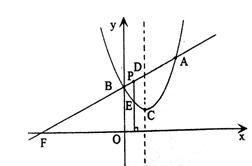 得以点P、E、D为顶点的三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
得以点P、E、D为顶点的三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
2007年河北省
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com