
题目列表(包括答案和解析)
2.下列命题中错误的是( )
A.两组对边分别相等的四边形是平行四边形 B.对角线相等的平行四边形是矩形
C.一组邻边相等的平行四边形是菱形 D.一组对边平行的四边形是梯形
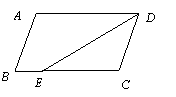
1.如图,在□ABCD中,已知AD=8㎝, AB=6㎝, DE平分∠ADC交BC边于点E,则
BE等于( )
A.2cm B.4cm C.6cm D.8cm

例1 如图2,已知在△ABC中,AD、CE为高,求证:△BDE∽△BAC.
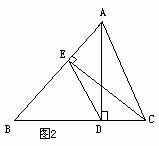 分析:首先凸显△BAD和△BCE,可证明相似,即可得到比例式
分析:首先凸显△BAD和△BCE,可证明相似,即可得到比例式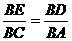 ,进而再凸显△BDE和△BAC,可根据两边对应成比例且夹角相等,两三角形相似.
,进而再凸显△BDE和△BAC,可根据两边对应成比例且夹角相等,两三角形相似.
证明:∵AD、CE为高,
∴∠ADB=∠BEC=900
在△BAD和△BCE中 ………(凸显思想的符号化表示)
∵∠ADB=∠BEC,∠B=∠B
∴△BAD∽△BCE
∴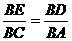
在△BDE和△BAC中 ……… (凸显思想的符号化表示)
∵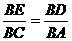 ,∠B=∠B
,∠B=∠B
∴△BDE∽△BAC
例2 如图3,平行四边形ABCD中,直线EF∥AB,在EF上任取两点E、F,连结AE、BF、DE、CF,分别交于G、H,连结GH.
求证:GH∥BC
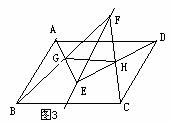 分析:本例如何探寻“中间比”来过渡“
分析:本例如何探寻“中间比”来过渡“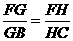 ”是证题的关键,可分别凸显△BAG和△FEG,△DCH和△EFH,即可得“中间比
”是证题的关键,可分别凸显△BAG和△FEG,△DCH和△EFH,即可得“中间比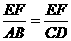 ”
”
证明:∵四边形ABCD为平行四边形,
∴AB∥CD,AB=CD.
又∵EF∥AB,
∴AB∥EF∥CD.
∴△BAG∽△FEG,△DCH∽△EFH. …………(凸显思想的体现)
∴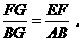
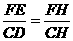 .
.
∴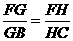
即GH∥BC
例3
如图,E、F为△ABC边AB、AC上两点,且AE=AF,连结EF并延长交BC的延长线于D点,求证: .
.
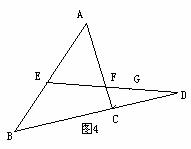
分析:对所证比例式分析后,容易想到从点C处引平行线,沟通已知条件和结论之间的联系.
证明:过点C 作CG∥BA,交DE于G,
 ∴△BAG∽△FEG,△DCH∽△EFH……(凸显思想的体现)
∴△BAG∽△FEG,△DCH∽△EFH……(凸显思想的体现)
∴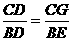 ,
,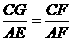
又∵AE=AF,
∴CF=CG
即 .
.
例4 如图5,路边有两根电线杆相距4米,分别在高为3米的A处和6米的C处用铁丝将两杆固定,求铁丝AD与铁丝将两杆固定,求铁丝AD与铁丝BC的交点M处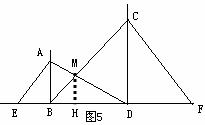 离地面的高MH.
离地面的高MH.
分析:要求MH的值,先行探究MH与AB、CD之间的关系,即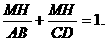
解:由题意,AB∥MH∥CD
∴△DMH∽△DAB,△BMH∽△BCD……(凸显思想的体现)
∴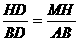 ①,
①,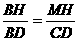 ②
②
①+②得: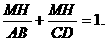
∴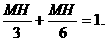
∴MH=2米.
即M离地面的高MH=2米.
凸显图形是一种思想,也是一种意识,要求同学们在今后的学习过程中能通过练习,多积累一些基本图形、常见图形及其性质,这样才能在解题中一路高歌、过关斩将.
其实初中几何中,最典型的凸显图形思想莫过于在全等三角形的学习,如图1:
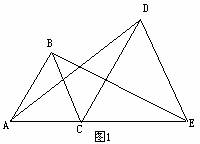 在△ACD和△BCE中
在△ACD和△BCE中
∵AC=BC,∠ACD=∠BCE,CD=CE
∴△ACD≌△BCE(SAS)
其中语句“在△ACD和△BCE中”即为凸显的最典型应用.
18.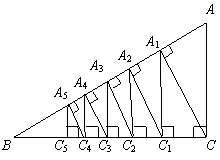 如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作
如图,已知直角三角形ACB,AC=3,BC=4,过直角顶点C作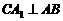 ,垂足为
,垂足为 ,再过
,再过 作
作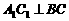 ,垂足为
,垂足为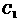 ;过
;过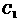 作
作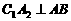 ,垂足为
,垂足为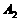 ,再过
,再过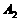 作
作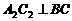 ,垂足为
,垂足为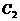 ;……,这样一直做下去,得到一组线段
;……,这样一直做下去,得到一组线段 ,
, ,
,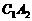 ,……,则第10条线段
,……,则第10条线段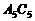 =_______________.
=_______________.
17.关于x的一元二次方程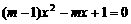 一两个不相等的实数根,则m的取值范围是_______________________.
一两个不相等的实数根,则m的取值范围是_______________________.
16.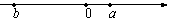 已知实数a、b在数轴上的位置如图所示,则以下三个命题:(1)
已知实数a、b在数轴上的位置如图所示,则以下三个命题:(1)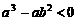 ,(2)
,(2)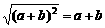 ,(3)
,(3)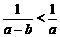 ,其中真命题的序号为_________________.
,其中真命题的序号为_________________.
15.已知不等式组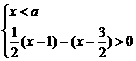 的解集为
的解集为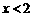 ,则a的取值范围是_____________.
,则a的取值范围是_____________.
14.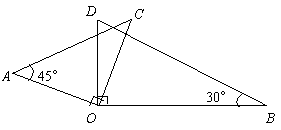 将一副直角三角板按图示方法放置(直角顶点重合),则
将一副直角三角板按图示方法放置(直角顶点重合),则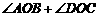 =____.
=____.
13.计算: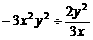 =__________.
=__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com