
题目列表(包括答案和解析)
1.已知一次函数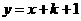 的图像经过原点,则k的值为………………( )
的图像经过原点,则k的值为………………( )
(A)1; (B)-1; (C)0; (D)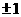 .
.
|
考 点 |
要 求 |
|
2.一次函数的概念 |
II |
|
3.用待定系数法求一次函数的解析式 |
II |
|
4.画一次函数的图像 |
II |
|
5.一次函数的图像及基本性质 |
III |
|
6.一次函数的应用 |
III |
函数与分析(2)
(一次函数)
4.通过实例分析以及正比例函数、反比例函数、一次函数等案例,理解函数的意义,知道函数的表示方法有解析法、列表法、图像法、知 道符号“y=f(x)”的意义。有关求函数值的问题,不涉及繁复的计算;关于函数的值域,只
道符号“y=f(x)”的意义。有关求函数值的问题,不涉及繁复的计算;关于函数的值域,只 要求了解其含义,不涉及求值域的问题。
要求了解其含义,不涉及求值域的问题。
3.选取实例讨论一次函数的实际应用,初步认识函数模型。
2.会画一次函数的图像,并借助图像直观,认识和掌握一次函数的性质。
1.以实例为背景引入一次函数,理解一次函数的概念,建立一次函数、二元一次方程、直线之间的联系;掌握直线平移与一次函数解析式y=kx+b中的b 间的关系。从中感知辩证的观点,进一步体会数形结合思想。
八年级第二学期:第二十章 一次函数(9课时)
25.如图,已知,在等腰△ABC中,AB=AC=5,BC=6.点D为BC边上一动点(不与B点重合),过D作射线DE交AB边于E,使∠BDE =∠A.以D为圆心,DC的长为半径作⊙D.
(1)设BD=x,AE =y,求y关于x的函数关系式,并写出定义域;
(2)当⊙D与AB边相切时,求BD的长;
 (3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD为何值时,⊙D与⊙E相切?
(3)如果⊙E是以E为圆心,AE的长为半径的圆,那么当BD为何值时,⊙D与⊙E相切?
24.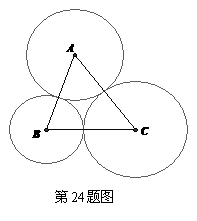 如图:⊙A、⊙B、⊙C两两外切,
如图:⊙A、⊙B、⊙C两两外切,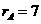 ,
,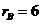 ,
,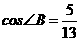 ,求:
,求:
23. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,O是BC边上一动点,O不与B、C重合,以O为圆心的半圆与AB切于D点,设OD=x,OC=y.
如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,O是BC边上一动点,O不与B、C重合,以O为圆心的半圆与AB切于D点,设OD=x,OC=y.
(1)求y与x的函数关系式并写出定义域;
(2)当x为何值时,半圆与AC相切.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com